Методика обучения доказательствам. Аналитический и синтетический методы доказательства. Доказательство «от противного».

Методика обучения док-вам.

Для того чтобы воспитать у учащихся потребность в ма­тематических доказательствах, нужно, чтобы они понимали, что в математике оперируют с утверждениями такого вида: «если что-то является тем-то, то что-то другое следует из этого». Например, если а 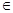N, b 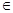N, то [(а+b) (2а + b)] 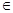N. Как это доказать? Что означает сам термин «доказательство»? Для разных людей этот термин имеет различные значения. Для ребенка он, прежде всего, означает, что что-то необходимо сде­лать для проверки, подтверждения факта существования какого-нибудь объекта или явления, для математика термин «доказательство», конечно, более содержателен. Уже при введении первых теорем необходимо, чтобы школьники отчетливо пред­ставляли себе главные отличительные чер­ты и примерную структуру математичес­кого доказательства. Если перед школьни­ками поставлена задача доказать некоторые утверждения, они должны понимать, что:

1) допускаются истинными некоторые отношения и факты;

2) от условия к заключению строится логически последова­тельная цепочка предложений, каждое из них должно быть обосновано с помощью суждений, выраженных в условии, определений извест­ных понятий, аксиом или ранее доказанных утверждений;

3) заключение является последним звеном в цепочке этих ло­гически расположенных предложений.

Если допустить, что условие истинно, если истинна вся данная цепочка утверждений, то и заключение следует признать ис­тинным.

С этой точки зрения весьма полезны упражнения про­педевтического характера, способные как можно раньше рас­крыть перед учащимся эту структуру доказательства. В этом от­ношении немалые возможности заложены в учебном материале, относящемся к началам систематических курсов арифметики и ал­гебры. Таковы, например, упражнения вида «Дополнить приведен­ные доказательства математических утверждений, выполняя указан­ные выше требования, предъявляемые к математическим доказа­тельствам».

Аналитический и синтетический метод доказательства.

Методы научного исследования - анализ и синтез - широко используются в математике. Анализ – от неизвестного - к известному, от искомого к данному, от целого к частям. Синтез – от частей к целому. Бытовой пример: ребенок разбирает игрушку (анализ) и собирает (синтез). В процессе развития анализ стали понимать как способ мышления, при котором от следствия переходят к причине, породившей это следствие, а синтез – способ мышления, при котором от причины переходят к следствию. Синтез в чистом виде встречается редко, в основном он с элементами анализа. Анализ и синтез неотделимы друг от друга, они вместе образуют единый аналитико-синтетический метод, который широко применяется в математике, физике, химии и других науках. Различают три типа аналитико-синтетического метода: синтетический, аналитический и метод попеременного движения с обоих концов. Сущность аналитического метода – исходным пунктом обоснования утверждения является само утверждение, которое путем логически обоснованных шагов сводится к истинному утверждению. Сущность синтетического метода – отыскиваются такие истинные утверждения, которые путем логически обоснованных шагов можно было бы преобразовать в данное требуемое утверждение. Аналитический метод проявляется в следующих формах: восходящий анализ, нисходящий (несовершенный и метод от противного), типа фильтр, через синтез. Восходящий анализ - ищутся достаточные признаки справедливости заключения. Несовершенный анализ – отыскание необходимых признаков. Типа фильтр – подстановка и отбрасывание неправильного.

Метод доказательства от противного.

Часто непосредственное доказательство той или иной теоремы представляет большие затруднения. В то же время док-во теоремы, противоположной обратной бывает несложным. В наших случаях вместо прямой теоремы доказывают обратную ей, противоположную обратной. Однако вместо того чтобы говорить о замене доказ-ва данной теоремы, доказ-м теоремы противоположной обратной говорят о доказательстве «от противного».

Сущность док-ва от противного заключ-ся в следующем:

-делается предположение, противоположное тому, что треб-ся доказать;

-выясняется, что получается из сделанного предположения на основе известных теорем и аксиом;

-устанавливается противоречие, м/у тем, что получилось и тем, что известно из условия теоремы;

-делаем вывод: предположение неверно, а верно, что требуется доказать.