 |
Уравнения в курсе алгебры 7-9 класс.
|
|
|
|
В 7 классе углубляются сведения об уравнениях с одной переменной. Изучение материала пункта «Уравнение и его корни» начинается с введения определения «Уравнение с одной переменной». Дается задача: «На 2-х полках 40 книг, на верхней полке в 3 раза больше книг, чем на нижней. Сколько книг на нижн. полке. Решение: пусть Х - книг на нижней полке, тогда на верхней – 3Х. По условию на обеих полках 40 книг. Имеем равенство Х+3Х = 40. Это равенство содержит переменную. Такие равенства называют уравнением. Затем вспоминают свойство уравнений: если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному. Если обе части ур-ния умножить или разделить на одно и то же отличное от нуля число, то получится уравнение равносильное данному. Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится ур-ние равносильное данному.
В курсе алгебры 7 кл. вводятся определеиня:
Опр1:Равенство с переменной называется уравнением.
Опр2:Корнем уравнения называется значение переменной при котором уравнение обращается в верное равенство.
Опр3:Решить уравнение значит найти все его корни или доказать, что их нет.
Опр4:Уравнения, имеющие одни и теже корни называются равносильными.
Поскольку уравнения – это равенства, содержащее переменную, то оно может иметь корень, не иметь корней, иметь бесконечно много корней. В учебнике приводятся примеры и в ходе решений уравнений учащиеся приобретают навыки применения свойств.
В 7 классе вводится понятие линейного уравнения с одной переменной: Уравнение вида ах = b, где х – переменная, а и b – числа называется линейным уравнением с одной переменной. Линейное уравнение имеет единственный корень х=b/a.
|
|
|
В 7 классе продолжается решение задач методом составления уравнения. Кроме того учащиеся знакомятся с понятием «уравнение с двумя переменными», рассматривают три способа решения систем: графический, сложения, подстановки.
В 8 классе изучения уравнений представляет собой одну из важнейших задач курса. В связи с изучением рациональных дробей рассматриваются уравнения содержащие переменную в знаменателе. Вводятся определения:
Опр1:Уравнения, левая и правая части которых являются рациональными выражениями, называются рациональными уравнениями. Например: 2х+5=3(8-х) и т.д.
Опр2:Рацион. уравнение, в котором левая и правая части являются дробными выражениями, называется дробным.
Известно, что решение дробных рациональных уравнений возможно двумя основными способами: 1) из условия равенства дроби нулю f(x)/g(x)=0 => f(x)=0, g(x)≠0; 2) из условия равенства двух дробей с одинаковыми знаменателями: f1(x)/g(x)=f2(x)/g(x) => f1(x)=f2(x), g(x)≠0.
В курсе алгебры используется 2-ой способ. В учебнике четко выделен алгоритм решения таких уравнений:
«для решения дробного уравнения необходимо: 1) найти общий знаменатель дробей, входящих в уравнения; 2) заменить данное уравнение целым, умножив обе части на общий знаменатель; 3) решить полученное целое уравнение; 4) исключить из его корней те, которые обращают в нуль общий знаменатель».
Алгоритм закрепляют при решении уравнений. В курсе алгебры 8 важное место отводится изучению квадратных уравнений. В первую очередь учителю важно сформировать само понятие «квадратного уравнения».
Опр: квадратным уравнением называют уравнения вида: ax2+ bx + c = 0, где х – переменная, а,b,c – некоторые числа, причем а≠0.
Для формирования понятия квадратного уравнения или вместо коэффициентов в нем можно предложить таблицу.
| № | а | b | c | ax2+bx+c =0 |
| ? | ? | ? | 7x2-8x+5=0 | |
| ? | ? | ? | 9x2+3=0 | |
| -4 | ? | |||
| -6 | ? |
Затем учащиеся знакомятся со способами решения квадратных ур-ний: 1)выделением полного квадрата двучлена; 2) по формуле; 3) используя теорему Виета. Наибольшее применение находит решение кв. ур-ний по формуле: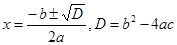 
|
|
|
На первых уроках необходимо вырабатывать навыки применения формулы. Учитель должен стремиться к тому, чтобы приведенные уравнения учащиеся решали по теореме Виета.
Теорема: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену, т.е. если x2+px+q=0 =>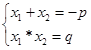 
Даная теорема дается с доказательством, а доказательство обратной теоремы не обязательно.
В 9 классе получают дальнейшее развитие понятия «уравнения в двумя переменными» и «системы уравнений с двумя переменными». Их решение осуществляется графическим способом и способом подстановки. В курсе алгебры неполной средней школы рассматривается простейшие уравнения с одной переменной, содержащим переменную под знаком модуля. К ним относятся уравнения вида: |ax+b|=c. Важно чтобы учащиеся понимали, что при решение таких уравнений надо различать случаи, когда с<0,c=0,c>0. Если с<0, то уравнение не имеет корней, если с=0, то уравнение |ax+b|=с равносильно ax+b=0. Если с>0, то уравнение |ax+b|=c равносильно дизъюнкции уравнений ax+b=c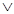 
ax+b=-c
Неравенства
Можно выделить два основных пути развертывания содержания линии неравенств:
1) Сначала изучается материал относящийся к уравнениям и их системам, затем к неравенствам. Раздельное изложение проводится до теории квадратного трехчлена включительно. Дальнейшее изучение, происходящее в старших классах лишено этого противопоставления: логарифмические, показательные, тригонометрические уравнения и соответствующие неравенства изучаются в более тесной связи с друг другом.
2) Основные классы неравенств изучаются сразу вслед за изучением соответствующих классов уравнений. Имеются и промежуточные пути, когда некоторые классы уравнений и неравенств сближены друг другом по времени изучения, а другие наоборот не связаны.
С 1985-1990 года неравенства изучались с 4 класса. С 1990 года в соответствии с новой программой по мат-ке теоретический материал о неравенствах дается в 8 классе. Особенности изучения неравенств: 1) как правило навыки решения неравенств, за исключением квадратных формируются на более низком уровне, чем навыки решения уравнений соответствующих классов. Эта особенность имеет объективную природу: теория неравенств сложнее теории уравнений; 2) большинство приемов решения состоит в переходе от данного неравенства а>b, к уравнению a=b и последующем переходе от найденных корней уравнения к множеству решений исходного неравенства (исключение составляют линейные неравенства); 3) в изучении неравенств большую роль играют наглядно-графические средства.
|
|
|
8 класс. Учащие знакомятся с числовыми неравенствами, определением большего числа, свойствами числовых неравенств. Затем рассматриваются неравенства с одной переменной, понятие числового промежутка, система неравенств. Знакомство учащихся с неравенствами дает возможность использовать аппарат неравенств при решении самых разнообразных задач.
В неполной средней школе из неравенств содержащих переменную под знаком модуля рассматриваются неравенства вида |x-a|<b, |x-a|>b. Решение таких неравенств связывается в понятием расстояния между точками координатной прямой. Например: пусть требуется решить неравенство |x-1|<5, т.к. под модулем |х-1| выражает расстояние между точками координатной прямой, координаты которых равны х и 1, то надо найти множество координат точек удаленных от точки с координатой 1 меньше, чем на 5 единиц. Т.е |x-1|<5 равносильно -5<x-1<5 => -4<x<6.
Метод интервалов.
1. Исходное неравенство приводится к виду р(х)/q(x)>0, где p(x) и g (x) многочлены
2. Разложить многочлен p(x) и g(x) на множители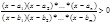 
3. Находим нули числителя и знаменателя
4. Если в разложении есть степень, то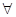 
нечетная степень заменяется первой степенью, четная степень опускается, но учитывается частное решение.
5. Нули числителя и знаменателя отмечают на числовой прямой
6. Проводят кривую знаков.
|
|
|
