Методика введения понятия «функция».

Слово «функция» происходит от латинского глагола fungi – выполнять, выражать, осуществлять. Различают два направления определения понятия «функция»: 1) с использованием понятия величины; 2) не используя этого понятия. В первом направлении выделяют два подхода: 1) функция как переменная величина, числовое значение которой меняется в зависимости от числового значения другой величины; 2) функция – это закон по которому значение независимой переменной соответствует значению зависимой переменной. Во втором направлении выделяют три подхода: 1) определяется не функция а ситуация; 2) определяют функцию как закон; 3) с помощью соответствия. Третий подход как принцип (каждому элементу области отправления соответственно равно один элемент области прибытия) положен в основу современного школьного понятия функции.

В процессе формирования понятия «функция» можно выделить несколько уровней:

1. Пропедевтический – начальная школа. На этом уровне не даются ни какие определения, однако материл начального курса математики содержит много примеров на которых можно разъяснить зависимость значения одной величины от значения другой. например можно показать как зависит сумма от каждого слагаемого, разность от уменьшаемого и вычитаемого и т.д. При этом используют так называемый язык «с пустыми местами» например 3 + …; 7 – …; … * 2 и т.д.

2. Пропедевтический – он отличается от первого тем, что составляется таблица значений, наглядно представляющие зависимость. Например: в пятом классе в теме «Буквенные выражения» и в дальнейшем учащимся предлагаются такие значения: отцу - х лет, сыну – у лет, отец старше сына на 30 лет – заполните пустые места в таблице, на этом уровне не даются не какие определения.

 

 

x	…		…
y		…		…	…

3. Пропедевтический курс алгебры 7 кл. начинается с изучения темы «Выражения в переменными». Решая задачу, учащиеся получают выражения с переменной: задача: двигаясь со скоростью 60 км/ч автомобиль пройдет за 2 часа – 60*2 км, за 3 – 60*3 км, за t часов – 60*t км. Выражение 60*t позволяет находить путь пройденный автомобилем за разные промежутки времени t. Букву t называют переменной, 60*t называют выражением с переменной.

Введение понятия функция начинается с решения задачи. Задача: расстояние между станцией и турбазой 60 км, с турбазы на станцию отправляется велосипедист со скоростью 12 км/ч. На каком расстоянии от станции он будет находиться через х часов. За х часов он пройдет 12*х км; (60-12х) км – расстояние на котором будет находиться через х часов велосипедист от станции. Обозначим расстояние буквой у, тогда у=60-12х. Мы получили формулу, выражающую зависимость расстояния у от времени движения х, по формуле у=60-12х для каждого значения х можно найти соответствующее значение у. Значение у зависит от значения х, причем каждому значению х соответствует единственное значение у. Такие зависимости одной переменной от другой называют функциональными зависимостями (функциями). Дается определение:

Зависимость переменной у от переменной х называет функцией, если каждому значению х соответствует (каждое) единственное значение у (аргумент). Переменную у называют зависимой переменной, область определение функции – это все значения, которые принимает независимая переменная. Затем необходимо вспомнить с учащимися примеры функциональных зависимостей рассмотренных ранее. (зависимость периметра квадрата от его стороны; зависимость скорости; пропорциональные и обратно пропорциональные переменные). Что бы задать ф-ию нужно указать способ с помощь которого для каждого значения аргумента можно найти соответствующее значение ф-ии.

Опр: графиком ф-ии называют множество всех точек, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям ф-ий. Даже учащиеся выясняют, что является графиком прямой пропорциональности у=kx, обратной пропорциональности y=k/x(7 кл.)

Методика изучения линейной функции.

В соответствии со схемой, изучения линейной ф-ии начинается с рассмотрения задач:

1. На шоссе расположены пункты А и В удаленные друг от друга на 20 км, мотоцикл выехал из В в направлении противоположном А со скоростью 50км/ч. За t часов мотоциклист проедет 50*t и будет находиться от А на расстоянии 50t+20км => зависимость этого расстояния от времени движения можно выразить ф-лой S=50t+20, где t≥0.

2. Ученик купил тетради по 3 коп за штуку и ручку за 35 коп. Какова стоимость всей покупки. Стоимость покупки зависит от числа тетрадей, если х – число тетрадей, а у –стоимость покупки, то у=3х+35. Вывод каждому х соответствует у, т.е. в обоих случаях мы встретились с функциями заданными формулами вида у=кх+в, где х – независимая переменная, к и в – некоторые числа. Такие функции называются линейными.

Опр: линейной функцией называется функция, которую можно задать формулой вида: у=кх+в, где х – независимая переменная, к и в - некоторые числа. Даже рассматривая конкретную функцию учащиеся выясняют, что является графиком линейной функции. Например, у=0,5х-2, составляют таблицу, отмечают точки на координатной плоскости. Без доказательства принимается, что графиком линейной функции является прямая. Необходимо научить учащихся строить график функции по двум точкам, по точкам пересечения функции с координатными осями. х=0, у=b; y=0, x=a. В ходе решения задач на построение графиков функций учащиеся проводят элементарные исследования, устанавливают свойства.

Практическое занятие №3

Тема: Изучение тригонометрических функций

Содержание практического занятия:

1. Первоначальное знакомство с тригонометрическими функциями в курсе геометрии 8 классе

2. Изучение тригонометрических функций в курсе алгебры 9 класса

3. Систематизация и расширение знаний о тригонометрических функциях числового аргумента в 10 кл; их свойства и графики

Литература: [1-4],[7], [11-16], [18]. Дополнительная литература I.[1-4]. Учебники алгебры, геометрии 7-11 класс

В математике тригонометрические функции часто опре­деляются аналитическим путем: с помощью степенных рядов, как решения дифференциального уравнения, как интегральные представления. Тригонометрические функ­ции могут быть определены геометрическими средствами. Существуют различные варианты изложения элементов тригонометрии в школьном курсе математики. Они основа­ны на применении системы координат, векторов, геомет­рических преобразований.

Традиционная методическая схема изучения тригоно­метрических функций такова: 1) вначале определяются тригонометрические функции для острого угла прямо­угольного треугольника; 2) затем введенные понятия обо­бщаются для углов от 0° до 180°; 3) тригонометрические функции определяются для произвольных угловых величин и действительных чисел.

Далее вводятся определения тригон. Ф. Конкретнее рассмотрим введение определения cos а, придерживаясь следующей мето­дической схемы: 1) построить на миллиметровой бумаге прямоугольный треугольник ABC; 2) обозначить величину острого угла А буквой а; 3) измерить (по клеткам) прилежащий катет АС и гипотенузу АВ; 4) вычислить отношение ; 5) записать значение cos а (делается следующая запись: cos a ..., в которой для а не ука­зывается его конкретное значение); 6) измерить транспор­тиром угол а, найти его величину и записать значение косинуса этого угла данного прямоугольного треугольни­ка; 7) проделать пп. 1—6 для острых углов других прямо­угольных треугольников. Определенные трудности в изучении элементов триго­нометрии порождает следующая теорема: «Косинус угла а зависит только от градусной меры угла». Необходимость изучения данной теоремы можно разъяснить учащимся следующим образом. Пусть требуется на основании определения найти cos 37°. Предположим что это задание выполняют отдельно друг от друга несколько человек. Чтобы найти cos 37°, они построят прямоугольный треугольник (каждый свой) с углом в 37° измерят прилежащий катет и гипотенузу, найдут отношение прилежащего катета к гипотенузе. Полученное число и будет являться cos 37°. Есть ли гарантия что каждый ученик получит один и тот же ответ? Этот[ вопрос возникает по той причине, что каждый ученщ строит свой прямоугольный треугольник, получает свое значения длин прилежащего катета и гипотенузы. Так может быть, и искомое отношение у каждого ученика буде какое-то свое? Понятно, что если бы значение cos 37^е при переходе от одного прямоугольного треугольника другому изменялось, то ценность такого понятия в математике была бы невелика. Изучаемая теорема является ответом на поставленные вопросы. Она утверждает, что' косинус острого угла зависит не от выбора прямоугольно­го треугольника, а только от меры угла.

При решении прямоугольных тре­угольников необходимо обратить внимание учащихся на тот факт, что с каждой из формул для cos a, sin а и tg а связываются еще две формулы:

Всего, таким образом, получается девять формул. Назовите (с учетом приведенных выше формул) основные виды задач на решение прямоугольного треугольника.

Разработайте опорный конспект для доказательства следующих тригонометрических тождеств:

sin² a +cos² a = 1, tg² a +1 = , 1 + =

sin (90° — a) = cos a, cos (90° — a) = sin a.

Определения косинуса, синуса и тангенса углов от 0° до 180° являются генетическими. В этих определениях указываются построения и вычисления, позволяющие най­ти значение тригонометрической функции. В пособии [23] говорится следующее: «До сих пор значения синуса, косинуса и тангенса были определены только для острых углов. Теперь мы определим их для любого угла от 0° до 180°. Возьмем окружность на плоскости ху с центром в начале координат и радиусом R. Пусть а — острый угол, который образует радиус ОА с положительной полуосью х. Пусть х и у — координаты точки А. Значения sin a, cos ос и tg а для острого угла а выражаются через координаты точки А. Именно:

cos a = 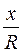Sin a= Tg a=

Определим теперь значения sin a, cos a и tg a этими формулами для любого угла а. (Для tg а угол а = 90° исключается.).

В курсе алгебры и начал анализа осуществляется последний, заключительный этап изучения тригонометри­ческих функций. В него входят: 1) закрепление пред­ставлений учащихся о радианной мере угла; отработка навыков перехода от градусной меры к радианной и наоборот; 2) формирование представлений об углах с градусной мерой, большей 360°; формирование представ­лений об углах с положительной и отрицательной градус­ными мерами; перевод этих градусных мер в радианы (положительные и отрицательные действительные числа); 3) описание тригонометрических функций на языке ра­дианной меры угла; 4) утверждение функциональной точки зрения на cos a, sin а и tg а (трактовка cos a, sin а и tg а как функций действительного аргумента, установление области определения, области значений, построение графика функции, установление промежутков монотонности, знакопостоянства и т. д.); 5) повторение известных и ознакомление с новыми тригонометрическими тождествами, ключом к которым является тождество cos (а + р) = cos а cos (3 — sin а sin (3 (формула косинуса суммы двух аргументов); 6) применение тригонометриче­ских тождеств в тождественных преобразованиях и при решении задач по стереометрии.

Практическое занятие №4

Тема: Уравнения и неравенства в курсе алгебры 8 класса.

Содержание практического занятия:

1. Квадратные уравнения в курсе алгебры 8 класса

2. Рациональные уравнения в курсе алгебры 8 класса

3. Неравенства второй степени в курсе алгебры 8 классе

Литература: [1-4],[7], [11-16], [18]. Дополнительная литература I.[1-4].

Изучение вопроса о квадратичной функции осуществляется в следующей последовательности, сначала изучается у=2x². Задача: найти зависимость площади поверхности куба от длинны его ребра. Пусть длинна ребра куба х см, площадь поверхности куба равна 6х² см², если обозначить х поверхности куба через у, то получаем равенство у=6x². В рассматриваемой задаче мы встретились с ф-ией, которая задается ф-лой у=ах², где х – независимая переменная, а – некоторое число. Итак рассмотрим ф-ию у=ах², выясним что является графиком этой ф-ии, каковы св-ва этой ф-ии:

1) при а=1, у=х² – графиком является парабола.

2) при а=1,5 у=1,5х². Составляют таблицу, строят график и рассматривая график учащиеся приходят к выводу, что график ф-ии у=1,5х² можно получить из параболы у=х², растяжением по оси х а полтора раза.

3) при а=0,5, у=0,5 х² – составляют таблицу, аналогично рассматривая график данной ф-ии

приходят к выводу, что график ф-ии у=0,5х² можно получить из параболы у= х² сжатием по оси х в два раза.

4) При а=-0,5, у=-0,5 х² – график ф-ии у=-0,5 х² может быть получен из графика ф-ии у=0,5 х² с помощью симметрии относительно оси х.

Вывод график ф-ии у=ах² при любом значении а≠0 называется параболой, затем:

1) при любом а, если х=0, то у=0 => график ф-ии проходит через начало координат.

2) при a>0, если х≠0, то у>0; при а<0, если х≠0, то у<0 (расположенные в координатной плоскости)

3) противоположным значениям аргумента соответствует равные значения ф-ии, следовательно график ф-ии симметричен относительно оси ординат

4) при a>0, у уменьшается при xє(-∞;0], увеличивается при xє[0;+∞), при а<0, у увеличивается при xє(-∞;0], уменьшается при xє[0;+∞). Точки пересечения параболы с ее осью симметрии называется вершиной параболы

График ф-ии y=ax²+bx+c

Рассматриваются, записанные на доске ф-ии y=x²-15x+8, y=-0,8x²+7x-15, учитель обращает внимание учащихся на то что правые части являются квадратными трехчленами, ф-ии называются квадратичными.

Опр: квадратичной ф-ией называется ф-ия, которую можно задать ф-лой y=ax²+bx+c, где х – независимая переменная, a,b,c – некоторые числа, причем а ≠ 0.

Для выяснения, что является графиком квадратичной ф-ии рассматривают пример: . Показывают, что график данной ф-ии может быть получет из графика ф-ии у=½х² с помощью параллельного переноса. Для этого выполняют некоторые преобразования: выделяют квадрат двучлена в правой части: , строят в одной сис-ме координат графики ф-ий у=½х² и у=½(х-5)²+3. Рассмотрим графики данных ф-ий. Учащиеся приходят к выводу, что любая точка графика у=½(х-5)²+3 может быть получена параллельным переносом соответствующих точек графика ф-ии , т.е. парал-ным переносом при котором всякая точка с координатами (х₀;y₀) переходят в точку с координатами (х₀+5;y₀+3). Из свойств параллельного переноса следует, что графиком ф-ии у=½(х-5)²+3, а значит и ф-ии является парабола, равная параболе у=½х². Далее рассматривают ф-ию в общем виде y=ax²+bx+c. В результате преобразований получают у=а(х+b/2а)² – (b²-4ас)/4а. Эта формула имеет вид y=a(x-m)²+n, m=(-b)/2a, n=(b²-4ас)/4а, можно докь-ть, что график функции y=a(x-m)²+n получился из графика ф-ии y=ax² с помощью пар. переноса при котором точка а с координатами (х₀;y₀) переходит в точку с координатами (х₀+m;y₀+n) => графиком ф-ии y=ax²+bx+c является парабола, равная y=ax² , ее вершиной является точка с координатами (m;n).

Для практики удобно строить график квадратичной ф-ии по нескольким точкам: 1) точки с координатами (m,n); 2) точки пересечения с осью Ох: y=0, ; 3) точка пересечения с осью Оу х=0, у=с. Далее рассматривают свойства функции: область определения функции, область значения функции, монотонность, точки пересечения с координатными осями, промежутки знакопостоянства, наибольшее и наименьшее значение ее.

Практическое занятие №5

Тема: Показательные и логарифмические уравнения и неравенства.

Содержание практического занятия:

1. Изучение показательных и логарифмических уравнений и их систем

2. Изучение показательных и логарифмических неравенств и их систем

Литература: [1-4],[7], [11-16], [18]. Дополнительная литература I.[1-4], II.

Практическое занятие №6

Тема: Изучение числовых последовательностей и прогрессий

Содержание практического занятия:

1. Место данной темы в ШКМ

2. Изучение прогрессий в курсе алгебры 9 класса

3. Виды упражнений

Литература: [1-4],[7], [11-16], [18]. Дополнительная литература I.[1-4], II, учебники и учебные пособия для учителя по алгебре 9 класса

Теория последовательностей занимает в школьном курсе мат-ки значительное место с простейшими примерами числовых последовательностей учащиеся встречаются при рассмотрении в курсе алгебры 9 кл. темы «Арифметические и геометрические прогрессии». Дальнейшее изучение бесконечных последовательностей, их пределов происходит в курсе алгебры и начала анализа 10 кл. в теме «Действительные числа» бесконечные последовательности и их пределы. Понятия последовательности и ее предела являются основным понятием математического анализа и находит важнейшее применение в различных вопросах школьного курса. Не используя указанных понятий нельзя достаточно строго и полно изложить в школе ряд вопросов алгебры и геометрии, например: вопросы о бесконечных десятичных дробях, о бесконечной прогрессии, о длине окружности, площади плоской фигуры, об объеме пирамиды и т.д.

Понятие последовательности вводится в курсе алгебры 9 кл. Причем общие сведения о последовательностях даются в том объеме, который необходим для изучения арифметической и геометрической прогрессии. Для введения понятия последовательности учащимся можно предложить выполнить следующие задания: выписать в порядке возрастания: а) положительные четные числа; 2 4 6 8 … б)положительные нечетные числа; 1 3 5 7 ….Получили последовательности чисел. Числа, образующие последовательности называют членами. Пронумеруем все члены последовательности по порядку: 1,2,3,4..,n,.. например 2,4,6,8,…2n; 1,2,3,4…n. Число а_n называют n-ным членом последовательности, саму последовательность обозначают (а_n). Последовательность может быть конечной и бесконечной. В ходе решения примеров, учащиеся знакомятся со способами задания последовательности: 1) ф-ла n-ного члена; 2) рекуррентным способом.

В этом случае для задания последовательности надо указать 1-ый член последовательности и рекуррентное соотношение выражающие n-ный член последовательности через предыдущий. Рассматривая различные последовательности выделяют те в которых каждый член начиная со второго получается прибавлением к предыдущему члену некоторого числа или умножением предыдущего члена на некоторое число и дают им особое название арифметическая и геометрическая прогрессии.

Практическое занятие №7

Тема: Методика введения понятия производной

Содержание практического занятия:

1. Определение производной

2. Задачи, приводящие к понятию производной

3. Производные элементарных функций

Литература:[1-4],[7],[11-16],[18]. Дополнительная литература I.[1-4], II, V.
учебники и учебные пособия для учителя по алгебре 10 класса

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: