Понятие последовательности и ее предела.

Теория последовательностей занимает в школьном курсе мат-ки значительное место с простейшими примерами числовых последовательностей учащиеся встречаются при рассмотрении в курсе алгебры 9 кл. темы «Арифметические и геометрические прогрессии». Дальнейшее изучение бесконечных последовательностей, их пределов происходит в курсе алгебры и начала анализа 10 кл. в теме «Действительные числа» бесконечные последовательности и их пределы. Понятия последовательности и ее предела являются основным понятием математического анализа и находит важнейшее применение в различных вопросах школьного курса. Не используя указанных понятий нельзя достаточно строго и полно изложить в школе ряд вопросов алгебры и геометрии, например: вопросы о бесконечных десятичных дробях, о бесконечной прогрессии, о длине окружности, площади плоской фигуры, об объеме пирамиды и т.д.

Понятие последовательности вводится в курсе алгебры 9 кл. Причем общие сведения о последовательностях даются в том объеме, который необходим для изучения арифметической и геометрической прогрессии. Для введения понятия последовательности учащимся можно предложить выполнить следующие задания: выписать в порядке возрастания: а) положительные четные числа; 2 4 6 8 … б)положительные нечетные числа; 1 3 5 7 ….Получили последовательности чисел. Числа, образующие последовательности называют членами. Пронумеруем все члены последовательности по порядку: 1,2,3,4..,n,.. например 2,4,6,8,…2n; 1,2,3,4…n. Число а_n называют n-ным членом последовательности, саму последовательность обозначают (а_n). Последовательность может быть конечной и бесконечной. В ходе решения примеров, учащиеся знакомятся со способами задания последовательности: 1) ф-ла n-ного члена; 2) рекуррентным способом.

В этом случае для задания последовательности надо указать 1-ый член последовательности и рекуррентное соотношение выражающие n-ный член последовательности через предыдущий. Рассматривая различные последовательности выделяют те в которых каждый член начиная со второго получается прибавлением к предыдущему члену некоторого числа или умножением предыдущего члена на некоторое число и дают им особое название арифметическая и геометрическая прогрессии.

Понятие предела последовательности является одним из важнейших мат-их понятий. При изучении этой темы учащиеся испытывают ряд трудностей. Основными из них является следующее:

1)само содержание темы(понятие предела связано с достаточно сложным понятием бесконечности). Само определение предела также трудно для восприятия: в определении используется неравенство с модулем, которое к тому же должно выполняться для всех n, больших некоторого N, и каждого ε>0. Необходимо отметить, что определение предела формулируется в непривычной для учащихся форме, а именно, предел есть число, которое связано с рассмотрением указанного выше неравенства. Более того указывается на конкретное число, а неравенство его определяющее.

2) изолированность темы от остальных тем курса и отсутствия пропедевтики в изучении этого вопроса в предшествующих классах

3) Различные отрицательные факторы внешнего порядка: недостаточное методическая разработанность темы, ограниченность временем на ее изучение.

В курсе мат. анализа существует несколько подходов к изучению этой темы:

а) метод (ε-δ), при котором определение предела дается на языке (ε-δ), док-во свойств и теорем о пределах ведется методом (ε-δ);

б) теория пределов может строиться на основе учения о бесконечно малых величинах;

в) при изучении теории пределов используются оба подхода: определение предела дается на языке (ε-δ), вводится понятие бесконечно малой, рассматривается теоремы о свойствах бесконечно малых, причем док-во ведется методом (ε-δ), далее рассматриваются св-ва пределов.

В учебном пособии алгебры и начала анализа 10-11 кл. введению определения предела последовательности предшествует рассмотрение примеров последовательности. Затем дается определение

Опр: Число х называется пределом последовательности (x_n), если для любого ε>0 при достаточно больших номерах n выполняется неравенство |x-x_n|< ε

Затем идет решение задачи вида: 1. Док-ть 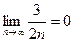2.Вычислить несколько членов последовательности (x_n), если x_n=(3n-1)/n

Задача на вычисление пределов идут после рассмотрения вопросов о пределе и непрерывности ф-ии в точке и теоремах о пределе. Однако практика показывает, что учащиеся испытывают трудности в усвоении данного определения, поэтому необходимо рассматривать серию дополнительных примеров и задач, которые будут способствовать формированию этого понятия. Изложение материала можно начать беседы.

Кроме того в определении предела последовательности необходимо обратить внимание на 2 момента:

1. Если последовательность имеет предел, т.е. 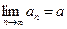, то недостаточно, чтобы для n→∞ для любого ε>0 разность |a_n-a| лишь один раз (т.е. для некоторого номера n=N₀) была меньше ε, надо чтобы разность |a_n-a| став меньше ε для n=N₀ и впредь оставалась бы меньше ε, при этом неравенство |a_n-a|<ε, должно выполняться для любого ε>0, а не для какого-то неопределенного;

2. Выбор номера N зависит от выбора ε;

уяснение этих положений хорошо провести на разборе задач. Например: док-ть

В учебнике алгебры и нач. анализа (1986) не рассматривается понятие – предел последовательности, а вводят понятие – предела функции, в п.14 «приближенное вычисление значений функции» учащиеся повторяют определения, известные из курса алгебры.

Опр: абсолютная погрешность приближенного значения х числа а наз. модуль разности между числом и его прибл. значением. Таким образом абс. погрешность приближенного равенства x≈a, есть число |x-a|.

Опр: Если абсол. погрешность приближенного значения х числа а не превосходит h, т.е. |x-a|≤h, то х называется приближенным значением числа а с точность до h.

Школьникам поясняют, что часто при вычислении значения ф-ии в точке а приходиться находить значение ф-ии не в самой (.)а, а в ближайшей к ней точке х. Например, если а=π, то для вычисления берем x=3,14 или х=3,1416 и т.д. При решении необходимо уметь оценивать точность проводимых вычислений.

Опр: Ф-ия f(x)→lim L при х→а если можно обеспечить любую наперед заданную точность h приближенного равенства f(x)≈L, за счет уменьшения погрешности ∆x=|x-a| значения аргумента.

Другими словами приближенного равенства f(x)≈L может выполняется с любой точностью, это же можно записать так: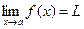

В теме производная рассматривается вопрос о мгновенной скорости движения.

Лекция №15-16

Тема: Изучение темы: «Первообразная и интеграл» в курсе алгебры и начал анализа

Содержание лекции

1. Место понятия «интеграл» В ШКМ

2. Введение понятия интеграл

3. Применение интеграла при решении геометрических и физических задач

Литература:[1-4],[7],[11-16],[18]. Дополнительная литература I.[1-4], II, V.
учебники и учебные пособия для учителя по алгебре 11 класса

Понятие интеграла в школе. Цель – ознакомить учащихся с интегрированием, как операцией обратной диф-ию, показать применение интеграла к решению геом задач. Место темы в программе: интеграл вводится на основе рассмотрения задач о площади криволинейной трапеции и построении интегральных сумм. Формула Ньютона – Лейбница вводится на основе наглядных представлений. Применяют интеграл при рассмотрении задач о вычислении площадей и объемов, формула объема шара используется в курсе геом. Методические особенности: при изучении темы целесообразно применять графические иллюстрации. Основные З и У: определение первообразной, простейшие правила нахождения первообразной. Введение понятия интеграла. Интеграл вводится с двух сторон: 1. Через криволинейную трапецию S(х) – есть функция от х, если х придать приращение D х, то получим площадь DS (х)»Dх* f(х), тогда f(х)»DS (х)/ Dх. Отсюда следует, что S^|(х)=f(х), то есть площадь есть первообразная от f(х)=> S(х)=F(b)-F(a) – приращение первообразной. 2. С другой стороны – площадь криволинейной трапеции рассматривается как интеграл S= интеграл от а до bf(х)dх. Из первого и второго получаем формулу Ньютона – Лейбница. Схема изложения интегралов в учебном пособии. 1. Площадь криволинейной трапеции как приращение первообразной непрерывной функции на отрезке: понятие криволинейной трапеции, теорема дающая один из подходов к задаче нахождения площади криволинейной трапеции. 2. Интеграл: второй подход к задаче нахождения площади криволинейной трапеции (предел суммы площадей прямоугольников), понятие интеграла как числа к которому стремятся суммы площадей прямоугольников при n -> к бесконечности. Устанавливается связь между интегралом и площадью криволинейной трапеции. 3. Формула Ньютона – Лейбница: сравнение результатов решения задачи о площади криволинейной трапеции при двух рассмотренных подходах дает данную формулу. При изучении данной темы следует широко использовать таблицы, кодопозитивы с изображением криволинейной трапеции, обращение записи решений и т.д. Обращается внимание учащихся на то, что понятие интеграла используется не только при вычислении площадей фигур, но и объемов тел. А также в задачах на вычисление пути за некоторый промежуток времени, если известна скорость, задачах о давлении в жидкостях и др.

Лекция №17-18

Тема: Первые уроки геометрии в 7 классе

Содержание лекции

1. Задачи преподавания геометрии в школе

2. Методика введения аксиом в курсе геометрии 7 класса

Литература: [1-4],[7],[11-16],[18]. Дополнительная литература I [1-4], II,IV,V.

Первые уроки планиметрии. Методика работы с аксиомами и теоремами.

Одна из целей включения аксиом в школьный учебник – сформировать базу для построения доказательств. Удачно подобранная система аксиом призвана обеспечить рациональное и простое построение всего курса. Аксиома - это мат. предложение, принимаемое без док. Они образуют систему отправных исходных положений. К системе аксиом предъявляются требования: независимости, непротиворечивости, целостности. Методическая схема введении аксиом:1.ввести аксиому на наглядной основе; 2.сформулировать аксиому; 3. выполнить логический анализ формулировки аксиом.; 4. провести математический. диктант. Математическое положение, истинность которого устанавливается посредством доказательства наз.теоремой, в Т. указано при каких условиях рассматривается объект (условие Т.), что об этом в Т-е утверждается (заключение). Формулировка Т может быть условной (если, то) и категорической. Доказательство - это организованная система предложений, каждая из кот является.либо аксиомой, либо выводится из 1-го или нескольких предложений по правилам логики. Под обучением доказательства понимают обучение мыслительным процессам поиска нахождения и построения доказательства. Этапы работы над Т.:1.мотивация необходимости изучения и раскрытия содержания 2.работа над структурой З.мотивация необходимости доказательства 4.построение чертежа и краткая запись условия Т. б.поиск доказательства, доказательство, запись.6.работа по закреплению Т.7.применение Т. Методы док.: аналитический (сведение к известному утверждению), синтетический (приведение к данному утверждению), аналитико-синтетический, от противного.

Лекция №19-20

Тема: Изучение темы «Окружность и круг»

Содержание лекции

1. Первое знакомство с окружностью и кругом в курсе математики начальной школы и 5 классе

2. Изучение темы «Окружность и круг» в курсе геометрии 7 кл

3. Изучение темы «Окружность и круг» в 9 кл.

Литература: [1-4],[7],[11-16],[18]. Дополнительная литература I [1-4], II,IV,V.

Окружность и круг в школьном курсе геометрии: основные понятия, определения, теоремы, формулы. Методика обучения геометрическим построением с помощью циркуля и линейки. С геом-ми построениями уч-ся знакомятся в конце 7 кл. Но перед этим они изучают понятия окр-ти и круга. В процессе изучения темы уч-ся знакомятся с теорет-ими фактами, связанными с окр-ю, необходимыми для решения задач на построение и для изучения в дальнейшем некоторых вопросов курса, в частности многоугольников, вписанных в окр-ть и описанных около окр-ти. В связи с этим при рассмотрении теор-ого материала и решении задач, необходимо отработать такие вопросы, как рав-во радиусов одной окр-ти, перпендикулярность касательной и радиуса, проведенного в точку касания, положение центров вписанной в треугольник и описанной около треугольника окр-ей. Док-во теорем о центрах вписанной и описанной окр-ей и решение соответствующих задач позволяет обратить внимание уч-ся на важные с точки зрения дальнейшего применения св-ва серединного перпендикуляра к отрезу, биссектрисы угла, отрезков касательных, проведенных к окр-ти из общей точки, радиуса, перпендикулярного хорде. При изучении и закреплении теоремы об углах вписанных в окр-ть, следует обратить внимание на конфигурацию, связанную с вписанным в окр-ть прямым углом, поскольку в дальнейшем эта конфигурация будет часто встречаться уч-ся. Значительное внимание при изучении данной темы должно быть уделено формированию практических навыков построений с помощью циркуля и линейки при решении простейших задач. Кроме того, здесь формируются умения связанные с вычленением основных построений, необходимых для решения комбинированных задач. При решении задач на построение вопрос о существовании и количестве решений не ставиться; задача считается решенной если указана последовательность выполняемых операций и доказано, что получаемая таким образом фигура удовлетворяет условию задачи.

Лекция №21-22

Тема: Изучение темы «Четырехугольники»

Содержание лекции

1. Первое знакомство с четырехугольниками в курсе математики начальной школы.

2. Изучение темы в курсе геометрии в 8 класса.

Литература:[1-4],[7],[11-16],[18]. Дополнительная литература I [1-4], II, III, IV,V. Учебники геометрии 8 класса.

Методика изучения темы «Многоугольники» «Четырехугольники». В начальной школе пропедевтика темы, многоугольник как средство изучения арифметики и алгебры, 5-6 кл как объект изучения, 7-9 изучение многоугольников: треугольники, 4-хугольники, многоугольники, вводятся Т, формируются понятия «св-ва» и «признак». В 5 кл заучивают небольшое число правил и определений, сведения, полученные в начальной школе повторяются, систематизируются и углубляются. Рассматривают примеры. 4-х угольник вводится как простая замкнутая 4-х звенная ломаная или как часть плоскости, ограниченная такой ломаной. Выделяются выпуклые 4хугольники. Вводятся треугольники, прямоугольники, ромбы. Квадрат как 4хугольник, который одновременно является прямоугольником и ромбом или как частный вид прямоугольника. Формируется логическое мышление и восприятие. Свойства и признаки 4-угольников разных видов находят широкое применение при изучении многогранников и тел вращения. Материал данной темы построен на дедуктивной основе(всем вводимым фигурам дается определение). Цепочка определений: ломаная(вершины, звенья), простая ломаная, замкнутая ломаная, многоугольник(вершины, стороны, диагонали), плоский многоугольник, выпуклый многоугольник, правильный многоугольник, вписанный(описанный) многоугольник. Изложение материала лучше в виде беседы. Рассматривают ломаную, дают опр замкнутой ломаной (концы совпадают), дают опр многоугольника(простая замкнутая ломаная, у которой соседние звенья не лежат на одной прямой), вводятся понятия: вершина, сторона, диагональ, примеры выпуклого многоугольника, вводят опр: многоугольник наз выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону, затем док Т: сумма углов выпуклого пугольника= 180°(п-2). важным является понимание того, что из любой вершины м. провести п=3диагонали и что они разбивают п- угольник на п-2 треугольника, перед Т рассматривают задачи: сколько диагоналей можно провести, если n=4,5, 6, n N; на сколько треугольников они его разобьют. При введении понятия внешнего угла выпуклого многоугольника при данной вершине приводят рис на котором выделены все внешние углы, обращают внимание, что при каждой вершине 2 внешних угла= между собой. Вводят опр внешнего угла треугольника, причем, если сумма внутренних углов выпуклого многоугольника зависит от числа сторон, то сумма внешних углов не зависит. Формула суммы внешних углов выпуклого многоугольника вводится в задаче, изучение темы заканчивается рассмотрением вопроса о правильных многоугольниках, о многоугольниках, вписанных или описанных. Выпуклый многоугольник называется правильным, если у него все стороны и все углы равны, рассматриваются задачи.

Лекция №23-24

Тема: Изучение вопросов взаимного расположения прямых на плоскости в школьном курсе математики

Содержание лекции:

1. Первое знакомство с вопросом взаимного расположения прямых в курсе математики 1-6 классов

2. Методика изучения параллельности и перпендикулярности прямых на плоскости.

Литература: [1-4],[7],[11-16],[18]. Дополнительная литература I [1-4], II, III, IV. Учебники геометрии 7-9 класса.

Методика изучения параллельности на плоскости и в пространстве. Первая встреча с параллельными прямыми происходит в 6 классе. Это обусловлено в целях пропедевтики и рассмотрения координатной плоскости. Созданию образа || прямых служат наблюдения окружающей обстановки. Важное значение имеют: формирование практических умений построения || прямых с использование м линейки и угольника. Учащиеся знакомятся с признаком параллельности прямых. Вопрос о взаимном расположении прямых изучается одним из прямых в курсе планиметрии (7 класс), а поэтому требует особого внимания к разработке их содержания и методики их преподавания, уже при изучении этих разделов целесообразно в доступной форме раскрывать роль основных свойств (аксиом). Создавать первые представления об аксиомах как о рабочем инструменте. Большая роль отводится аксиоме «через любые две точки можно провести прямую и только одну». Учение о параллельности в курсе планиметрии можно разделить на следующие части: определение || прямых, существование || прямых, построение || прямых, аксиома || прямых, свойства ||, признаки || - ти, применение изученной теории в решении задач. Последний раздел присутствует во всех предыдущих. В 8 классе изучается теорема Фалеса и на ее основе свойства средней линии треугольника и трапеции. Параллельность прямых в пространстве. Основная цель – дать учащимся математические знания о ||-тти Е1 и Е2 в Е3. в теме продолжается знакомство со взаимным расположение Е1 и Е2 в Е3. Рассматривается ||-ть прямых, Е1 и Е2, 2х Е2. Для всех этих случаев даются соответствующие определения и признаки, обсуждаются вопросы существования и!. Теоремы сущ-ия доказ-ся конструктивно, что дает учащимся конкретный способ построения Е1 или Е2. Позднее учащиеся знакомятся с одним признаком параллельности плоскостей «Две Е2 ||, если они имеют общий перпендикуляр». В теме обобщаются известные из планиметрии сведения о параллельных прямых. На примере теоремы о существовании и ед-ти прямой || данной Е1, учащиеся получают представления о необходимости заново доказывать известные им из планиметрии факты в тех случаях, если речь идет о точках и прямых Е3, а не конкретной плоскости. Задачи на доказательство решаются во многих случаях конструктивно. В связи с появлением задач на вычисление длины отрезка возникает необходимость целенаправленного повторения планиметрического материала: оперд, свойств признаков параллелограмма, равенство и подобие треугольников и т.д. При решении задач учащиеся должны использовать их в качестве аргумента при обосновании определения признаков параллельности. Теорема о пресечении двух || Е2 третьей Е2 и о пересечении 2х || Е2 2я ||Е1.Темы играют важную роль в процессе формирования пространственных представлений учащихся. Изучение теоретического материала сочетается с решением задач на построение с использованием моделей и рисунков. В теме рассматривается пункт «Изображение пространственных фигур на плоскости». При изучении параллельности в пространстве возникает ряд методических вопросов без решения которых нельзя добиться хороших результатов наиболее важным их них является набор упражнений по теме. Здесь много теорем и следствий из них. Без выполнения упражнений не будет достигнута главная цель, развитие пространственного воображения. Часть упражнений имеет форму вопросов и ставит своей целью уточнение. Правильно. Правильно – ли учащиеся понимают упражнения, аксиомы. Группа один при всей простоте эти упражнения вызывают интерес у учащихся, требуют для получения ответа выполнения схематических рисунков, привлечения моделей. Важно при решении этих упражнений добиться обоснования ответов. Группа 2 связана с рассмотрением || Е1 и Е2 на готовых чертежах.. Группа 3: задачи на вычисление При решении таких задач используются признаки подобия треугольников, теорема Фалеса, свойства средней линии треуг., трапеции. Группа 4 задачи на доказательство Группа 5 задачи на построение (воображаемое на проекционном чертеже). Различие этих задач подчеркивается словами «провести» - доказать существование, «построить» - обосновать на чертеже (– воображаемое, – проекционный чертеж).

Методика изучения перпендикулярности (пер) на Е2 и Е3. Учение о пер-х прямых начинается в 6 классе на интуитивной основе. Изучение пер прям идет в одном классе с || Е1 и взаимосвязаны. В своей основе пер Е1 имеет понятие «угол между Е1». Величиной наименьшего из углов образованного двумя пересекающимися прямыми считают углом между ними. То есть угол между пересекающимися Е1 не может превосходить 90 градусов. В случае, когда угол равен 90 градусов прямые называются пер. Существование пер Е1 показываются конструктивно, даются понятия: серединный пер и наклонная. Методика перпендикулярности в Е3. Основная цель: дать учащимся систему сведений о пер Е1 и Е2 в Е3. Продолжается изучение взаимного расположения Е1и Е2 в Е3. Рассматривается пер прямых, Е1 и Е2, 2х Е2. Материал темы обобщает и систематизирует сведения о пер Е1. При изучении темы возрастает роль задач на вычисление, широко используется теорема Пифагора, теорема о 3х пер, теорема о пер плоскостях. Темой является пропедевтической для изучения многогранников. При решении многих задач, связанных с вычислением длин пер и наклонных е2. речь идет о вычислении элементарных пирамид. Доказывается теорема выражающая признак пер Е1 и Е2. Из изучаемых свойств содержательными являются теорема выражающая зависимости между ||-ью и пер-ью прямых и плоскостей. Теорема: если Е2 пер одной из 2х || Е1, то она пер и другой. Теор. – две Е1 прямые пер одной и той же Е2, то они ||. Во многих учебниках предлагается начинать систематизированный курс стереом - ии с темы «Пер в Е3». В качестве основного аргумента в пользу расположения материала выдвигается возможность решения многих задач ан вычисление начиная с первых уроков геометрии. Сторонники противоположной т.з. отмечают, что задачи на вычисление с успехом могут быть заманены док –ом. В то время как изложение теор-го материала в случае раннего изучения ||-ти выглядит более доступным и имеет ряд преимуществ. Также введение в программу таких вопросов, как ||-ое проектирование, изображение фигур требует знания ряда фактов раздела параллельности. Таким образом принятый порядок изучения в школе: параллельности, затем пер-ти является целесообразным.

Лекция №25-26

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: