Главная | Обратная связь | Поможем написать вашу работу!

Методика введения понятия производной. Приложения производной.

Введению понятия производной функции может предшествовать рассмотрение задач. Такими задачами являются: задачи о мгновенной скорости прямолинейного движения тела, мгновенной величине тока, теплоемкости тела в точке. В алгебре и началах анализа 10-11 кл. понятие производной вводится в =>-щей последовательности: 1) Рассматривается понятие приращения аргумента и приращения функцции, 2) Вводят определение функции дифференцируемой в точке А. Функция f называется дифференцируемой в точке А если ее приращение при переходе от А к А+Н может представить в виде f(A+H)-f(A) = (K+L)H (1), где К- число, L-ф-ция -малая при Н стрем. к О, 3)Производная ф-ции f в наз-ся ф-ция f ' значение которой

lim a = 0 в точке x выр-ся фор-лой f(x + H)-f(x): f ' (х)= lim = Н, т.е. значение производной от ф-ции f в точке X равно пределу отношения приращения ф-ции к приращению аргумента, если приращение аргумента Для того чтобы найти значение производной ф-ции f в точке X надо: 1)найти выражение для приращения f(x+H)-f(x) ф-ции f; 2) разделить отображение на приращение аргумента Н; 3}найти предел полученного отношения при Н—О.

В школьном курсе математики рассматривают применение производной к приближенным вычислениям. В геометрии, физике применение производной к исследованию функций. Сюда относятся решение дробно-рац-ных нер-в методом интервала, задачи на нахождение наиб-го и наименьшего значения функции.

Метод интервалов. Решение дробно-рациональных неравенств вида P(x)/Q(x)< >0, где P(x),Q(x) некоторые многочлены удобно решать методом интервала. Дроб-рац-ное нер-во после выполнения тождественных преобразований приводится к виду: P(x)/Q(x)< >0. Затем Р(х) и О(х) раскладываются на множители, тогда неравенство принимает вид: . По основному свойству дроби числитель и знаменатель умножают на произведение (x-b₁)(x-b₂)#0.

Умножим обе части неравенства на произведение (x-b1)²{x-bn)². Находим критические точки в которых числитель =0. Если в какой-то из этих точек знаменатель не существует то эти точки б/исключены из решения. Полученные точки располагают на координатной прямой и определяют знак на крайнем справа интервале, выбирая промежутки удовлетворяющие неравенству. Исследование функции на монотонность, нахождение наиб. и наим. значения.

Практическое занятие №8

Тема: Изучение геометрического материала в 1-6 кл

Содержание лекции

1. Цели изучения геометрического материала в 1-6 классах

2. Методика изучения элeмeнтов геомeтрии

Литература: [1-4],[7],[11-16],[18]. Дополнительная литература I [1-4], II,IV,V.

Изучение геометрического материала в V классе имеет целью обобщить полученные учащимися в I - IV классах представления о простейших геометрических фигурах, а также познакомить учащихся с новыми геометрическими понятиями. В VI классе большое внимание уделяется систематизации геометрического материала. В пропедевтическом курсе геометрии формируется умения и навыки геометрических построений с помощью линейки, циркуля, чертежного треугольника и транспортира.

Введение и формирование геометрических понятий в V-

VI классах осуществляется на основе индуктивных рассуждений, требующих от начинающего учителя владения соответствующими приемами обучения:

1) выполнение мыслительных операций анализа, синтеза, обобщения, абстрагирования и др.;

2) сосредоточение внимания учащихся на существенные признаки изучаемого понятия;

3) выявление логической структуры признаков вводимого понятия;

4) определение понятий через род и видовые отличия, через описание процесса его образования;

5)построение объекта по существенным признакам понятия

6) дополнительные построения с целью получения объектов, принадлежащих к данному понятию;

7) рассмотрение объекта в плане разных понятий и др.

Будущий учитель должен знать признаки

сформированности геометрических понятий у учащихся. К ним относится в основном следующая совокупность умений учащихся:

а) умение самостоятельно выделять существенные признаки объекта;

б) давать определение понятию;

в) строить объект, исходя из существенных признаков понятия;

г) выполнять дополнительные построения с целью получения объекта, принадлежащего данному понятию и др.

Формируются указанные умения в основном с помощью задач. При этом будущий учитель должен знать, что ряд геометрических понятий пропедевтического курса геометрии получает генетическое определение (описанием процесса их образования).

Геометрические понятия, как отрезок, луч, равносторонний треугольник, координатный луч, равные фигуры, площадь прямоугольника и квадрата, объем прямоугольного параллелепипеда, окружность, дуга окружности, сектор, угол, равные углы, длина окружности, площадь круга, определяются описанием процесса их образования т.е.генетически.

Геометрические понятия, как, длина ломаной, периметр многоугольника, квадрат, круг, биссектриса угла, развернутый угол, прямой угол, градус, острый угол, тупой угол, перпендикулярность и параллельность прямых и др. определяются через видовые отличия т. е. через род.

В учебниках имеет место еще один способ определения - описание понятия. Под описанием понятия имеют в виду перечисление всех его элементов. Нестрого под описанием понимают выражение содержания с помощью понятий, не являющихся предшествующими и используемых индуктивно.

Практическое занятие №9

Тема: Изучение темы «Признаки равенства треугольников»

Содержание практического занятия

1. Первое знакомство с треугольников в начальной школе

2. Место темы в курсе геометрии 7 класса

3. Изучение доказательств признаков равенства треугольников

Литература: [1-4],[7],[11-16],[18]. Дополнительная литература I [1-4], II,IV,V.

Треугольник — самый «экономный» вид многоугольника. Для его задания достаточно указать его вершины — три точки, не лежащие на одной прямой, или три попарно пересекающиеся прямые. Классифицируют треугольники также по степени их симметричности или по числу равных сторон.

Треугольник	Количество осей симметрии	Количество парравных сторон
Равносторонний
Равнобедренный
Разносторонний	Нет	Нет

В школе принята также классификация треугольников по углам: остроугольные, прямоугольные и тупоугольные.

Изучение треугольников в соответствии с программой распределено практически по всем классам неполной средней школы. Курс VI класса — это, по существу, геометрия треугольника. Треугольник — одна из основных «рабочих» фигур изучаемого в школе курса планиметрии. Установление цепочек равных треугольников — широко используемый прием доказательства различных геометрических утверждений.

На изучение признаков равенства треугольников отводится 12 ч: (один из них резервный). Главная цель изучения этого материала — добиться активного владения им, обратив особое внимание на отработку навыков использования признаков равенства треугольников в решении задач. Равенство треугольников традиционно изучается в курсе планиметрии. В соответствии с определением, данным в учебнике А. В. Погорелова, в равных треугольниках ABC и А1В1С1 имеем шесть пар соответственно равных элементов: АВ — А₁В₁, ВС = В₁С₁, АС = А₁С₁, A= A₁, B= B₁, C= C₁.Внимание к записи равенства треугольников (буквы, обозначающие соответственные вершины, должны занимать одинаковые позиции в обозначении треугольников) позволяет: 1) имея запись равенства треугольников, например 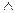АВС= 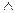PQR, почти автоматически делать вывод о равенстве соответственных сторон и углов, т. е. по определению будем иметь: 1)AB = PQ, BC = QR, AC = PR, A = P, B= Q. AC— /L.R; 2) существенно опираться на запись равенства треугольников при доказательстве равенства углов при основании в равнобедренном треугольнике и теоремы, обратной ей. Учителю необходимо следить за правильностью буквенной записи равенства треугольников. Характерным для учебного пособия является и наличие в нем аксиомы существования треугольника, равного данному (которая, по существу, является эквивалентом аксиомы подвижности плоскости). Важным на начальном этапе рассмотрения равных треугольников является отработка понятий «сторона, противолежащая углу», «угол, заключенный между сторонами». Программа диктует необходимость уже с самого начала изучения систематического курса планиметрии проводить работу по логическому развитию учащихся, по формированию и развитию таких понятий, как «свойство» и «признак». Доказательство первых двух признаков равенства треугольников в учебном пособии сводится к доказательству совпадения некоторого третьего треугольника, равного первому и определенным образом расположенного относительно второго, с этим вторым данным треугольником. При доказательстве первых двух признаков равенства можно использовать серию рисунков (кодопозитивов), отражающих динамику доказательства, отдельные его этапы. Так, при рассмотрении первого признака полезно использовать серию рисунков. При использовании признаков равенства треугольников: 1) указывается пара треугольников, относительно которых выдвигается гипотеза об их равенстве; 2) в рассматриваемых треугольниках выделяются пары соответственно равных элементов; 3) на основании одного из признаков делается вывод о равенстве рассматриваемых треугольников; 4) делают вывод о равенстве каких-либо из соответственных элементов. При обучений решению задач на применение признаков равенства треугольников целесообразно использование готовых чертежей, на которых отмечены равные элементы. Теорема Пифагора позволяет широко применять в обучении геометрии Тмётод" координат и другие аналитические методы. Тесно связано с этой теоремой рассмотрение тригонометрических функций острого угла прямоугольного треугольника. Очень важным в раскрытии геометрии треугольника является вопрос о подобии треугольников как конкретизации общего понятия подобных фигур. Этот материал важен с точки зрения формирования представлений о форме фигуры.

Практическое занятие №10

Тема: Изучение задач на построение с помощью циркуля и линейки

Содержание практического занятия:

1. Цели обучения решению задач на построение

2. Основные задачи на построение с помощью циркуля и линейки

3. Схема решения сложных задач на построение с помощью циркуля и линейки.

Литература: [1-4],[7],[11-16],[18]. Дополнительная литература I [1-4], II,IV,V. Учебники геометрии 7-11 класса.

⇐ Предыдущая 9 10 11 12 131415 16 17 18 Следующая ⇒

Воспользуйтесь поиском по сайту: