Колебания системы хищник—жертва

Еще в 20-х гг. А. Лотка (Lotka, 1925), а несколько позднее независимо от него В. Вольтерра (1976) предложили математические модели, описывающие сопряженные колебания численности популяций хищника и жертвы. Рассмотрим самый простой вариант модели Лотки—Вольтерры. Если предположить, что популяция жертв в отсутствие хищника растет экспоненциально, а пресс хищников тормозит этот рост, причем смертность жертв пропорциональна частоте встреч хищника и жертвы (или иначе, пропорциональна произведению плотностей их популяций), то мгновенная скорость изменения численности популяции жертв dN₁/dt может быть выражена уравнением — dN₁/dt = r₁N₁ – p₁N₁N₂, где r₁ — удельная мгновенная скорость популяционного роста жертвы, p₁ — константа, связывающая смертность жертв с плотностью хищника, a N₁ и N₂ — плотности соответственно жертвы и хищника. Мгновенная скорость роста популяции хищника в этой модели принимается равной разности рождаемости (которая в свою очередь зависит от интенсивности потребления хищником жертв) и постоянной смертности:

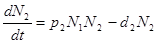
где р₂. — константа, связывающая рождаемость в популяции хищника с плотностью жертв, а d₂ — удельная смертность хищника (принимаемая постоянной). Согласно приведенным уравнениям каждая из взаимодействующих популяций в своем увеличении ограничена только другой популяцией, т. е. рост числа жертв лимитируется прессом хищников, а рост числа хищников — недостаточным количеством жертв. Никакого самоограничения популяций не предполагается. Считается, например, что пищи для жертвы всегда достаточно. Также не предполагается и выхода из-под контроля хищника популяции жертв, хотя на самом деле такое бывает достаточно часто.

Несмотря на всю условность модели Лотки—Вольтерры, она заслуживает внимания уже хотя бы потому, что показывает, как даже такая идеализированная система взаимодействия двух популяций может порождать достаточно сложную динамику их численности. Решение системы этих уравнений (приводить которое мы здесь не будем) позволяет сформулировать условия поддержания постоянной (равновесной) численности каждого из видов. Популяция жертв сохраняет постоянную численность, если плотность хищника равна r₁/p₁ а для того чтобы постоянство сохраняла популяция хищника, плотность жертв должна быть равна d₂/p₂. Если на графике отложить по оси абсцисс плотность жертв N₁, а по оси ординат — плотность хищника N₂, то изоклины, показывающие условие постоянства хищника и жертвы, будут представлять собой две прямые, перпендикулярные друг другу и координатным осям (рис. 45, а). При этом предполагается, что ниже определенной (равной d₂/p₂) плотности жертв плотность хищника всегда будет уменьшаться, а выше — всегда увеличиваться. Соответственно и плотность жертвы возрастает, если плотность хищника ниже значения, равного r₁/p₁ и уменьшается, если она выше этого значения. Точка пересечения изоклин соответствует условию постоянства численности хищника и жертвы, а другие точки на плоскости этого графика совершают движение по замкнутым траекториям, отражая, таким образом, регулярные колебания численности хищника и жертвы (рис. 45, б). Размах колебаний определяется начальным соотношением плотностей хищника и жертвы. Чем ближе оно к точке пересечения изоклин, тем меньше окружность, описываемая векторами, и соответственно меньше амплитуда колебаний.

Одна из первых попыток получения колебаний численности хищника и жертвы в лабораторных экспериментах принадлежала Г. Ф. Гаузе (Gause, 1934). Объектами этих экспериментов были инфузория парамеция (Paramecium caudatum) и хищная инфузория дидиниум (Didinium nasutum). Пищей для парамеции служила регулярно вносимая в среду взвесь бактерий, а дидиниум питался только парамециями. Данная система оказалась крайне неустойчивой: пресс хищника по мере увеличения его численности приводил к полному истреблению жертв, после чего вымирала и популяция самого хищника. Усложняя опыты, Гаузе устраивал убежище для жертвы, внося в пробирки с инфузориями немного стеклянной ваты. Среди нитей ваты могли свободно перемещаться парамеции, но не могли дидиниумы. В таком варианте опыта дидиниум съедал всех парамеций, плавающих в свободной от ваты части пробирки, и вымирал, а популяция парамеции затем восстанавливалась за счет размножения особей, уцелевших в убежище. Некоторого подобия колебаний численности хищника и жертвы Г. Ф. Гаузе удалось добиться только в том случае, когда он время от времени вносил в культуру и жертву и хищника, имитируя таким образом иммиграцию.

Через 40 лет после работы Г. Ф. Гаузе его опыты были повторены Л. Лакинбиллом (Luckinbill, 1973), использовавшим в качестве жертвы инфузорию Paramecium aurelia, а в качестве хищника того же Didinium nasutum. Лакинбиллу удалось получить несколько циклов колебаний численности этих популяций, но только в том случае, когда плотность парамеций была лимитирована нехваткой пищи (бактерий), а в культуральную жидкость добавляли метилцеллюлозу — вещество, снижающее скорость движения как хищника, так и жертвы и потому уменьшающее частоту их возможных встреч (рис. 46). Оказалось также (Luc-kinbill, 1974), что добиться колебаний хищника и жертвы легче, если увеличить объем экспериментального сосуда, хотя условие пищевого лимитирования жертвы и в этом случае обязательно. Если же к системе сосуществующих в колебательном режиме хищника и жертвы добавляли избыточную пищу, то ответом был быстрый рост численности жертвы, за которым следовало возрастание численности хищника, приводящее в свою очередь к полному истреблению популяции жертвы. Строго говоря, те опыты Л. Лакинбилла, в которых удалось добиться сосуществования парамеции и дидиниума, не могут рассматриваться как подтверждающие модель Лотки—Вольтерры, поскольку рост численности жертв в этих опытах лимитирован не только хищником, но и нехваткой пищи.

Модели Л. Лотки и В. Вольтерры послужили толчком для разработки ряда других более реалистичных моделей системы хищник — жертва. В частности, довольно простая графическая модель, анализирующая соотношение разных изоклин жертвы и хищника, была предложена М. Розенцвейгом и Р. Мак-Артуром (Rosenzweig, MacArthur, 1963). Согласно этим авторам, стационарная (= постоянная) численность жертвы в координатных осях плотности хищника и жертвы может быть представлена в виде выпуклой изоклины (рис. 47, а). Одна точка пересечения этой изоклины с осью плотности жертвы соответствует минимальной допустимой плотности жертвы (ниже ее популяция подвержена очень большому риску вымирания хотя бы из-за малой частоты встреч самцов и самок), а другая — максимальной, определяемой количеством имеющейся пищи или поведенческими особенностями самой жертвы. Подчеркнем, что речь идет пока о минимальной и максимальной плотностях в отсутствие хищника. При появлении хищника и увеличении его численности минимальная допустимая плотность жертвы, очевидно, должна быть выше, а максимальная — ниже. Каждому значению плотности жертвы должна соответствовать некоторая плотность хищника, при которой достигается постоянство популяции- жертвы. Геометрическое место таких точек и есть изоклина жертвы в координатах плотности хищника и жертвы. Векторы, показывающие направление изменения плотности жертвы (ориентированные горизонтально), имеют разную направленность по разные стороны от изоклины (см. рис, 47, а).

Для хищника в тех же координатах также построена изоклина, отвечающая стационарному состоянию его популяции. Векторы, показывающие направление изменения численности хищника, ориентированы вверх или вниз в зависимости от того, по какую сторону от изоклины они находятся. Форма изоклины хищника, показанная на рис. 47, б, определяется, во-первых, наличием некоторой минимальной плотности жертвы, достаточной для поддержания популяции хищника (при более низкой плотности жертвы хищник не может увеличивать свою численность), а во-вторых, наличием некоторой максимальной плотности самого хищника, при превышении которой численность будет снижаться независимо от обилия жертв.

При совмещении изоклин жертвы и хищника на одном графике возможны три различных варианта (рис. 48). Если изоклина хищника пересекает изоклину жертвы в том месте, где она уже снижается (при высокой плотности жертв), векторы, показывающие изменение численности хищника и жертвы, образуют траекторию, закручивающуюся во внутрь, что соответствует затухающим колебаниям численности жертвы и хищника (рис. 48, а). В том случае, когда изоклина хищника пересекает изоклину жертвы в ее восходящей части (т. е. в области низких значений плотности жертв), векторы образуют раскручивающуюся траекторию, а колебания численности хищника и жертвы происходят соответственно с возрастающей амплитудой (рис. 48, б). Если же изоклина хищника пересекает изоклину жертвы в области ее вершины, то векторы образуют замкнутый круг, а колебания численности жертвы и хищника характеризуются стабильной амплитудой и периодом (рис. 48, в).

Иными словами, затухающие колебания соответствуют ситуации, при которой хищник ощутимо воздействует на популяцию жертв, достигнувшую только очень высокой плотности (близкой к предельной), а колебания возрастающей амплитуды возникают тогда, когда хищник способен быстро увеличивать свою численность даже при невысокой плотности жертв и таким образом быстро ее уничтожить. В других вариантах своей модели М. Розенцвейг и Р. Мак-Артур показали, что стабилизировать колебания хищник — жертва можно, введя «убежище», т. е. предположив, что в области низкой плотности жертв существует область, где численность жертвы растет независимо от количества имеющихся хищников.

Стремление сделать модели более реалистичными путем их усложнения проявилось в работах не только теоретиков, но и экспериментаторов. В частности, интересные результаты были получены Хаффейкером (Huffaker, 1958), показавшим возможность сосуществования хищника и жертвы в колебательном режиме на примере мелкого растительноядного клеща Eotetranychus sexmaculaus и нападающего на него хищного клеща Typhiodromus occidentalis. В качестве пищи для растительноядного клеща использовали апельсины, помещенные на подносы с лунками (вроде тех, что используются для хранения и перевозки яиц). В первоначальном варианте на одном подносе было 40 лунок, причем в некоторых из них находились апельсины (частично очищенные от кожуры), а в других — резиновые мячики. Оба вида клещей размножаются партеногенетически очень быстро, и поэтому характер их популяционной динамики можно выявить за сравнительно короткий срок. Поместив на поднос 20 самок растительноядного клеща, Хаффейкер наблюдал быстрый рост его популяции, которая стабилизировалась на уровне 5—8 тыс. особей (в расчете на один апельсин). Если к растущей популяции жертвы добавляли несколько особей хищника, то популяция последнего быстро увеличивала свою численность и вымирала, когда все жертвы оказывались съеденными (рис. 49, а).

Увеличив размер подноса до 120 лунок, в которых отдельные апельсины были случайно разбросаны среди множества резиновых мячиков, Хаффейкеру удалось продлить сосуществование хищника и жертвы. Важную роль во взаимодействии хищника и жертвы, как выяснилось, играет соотношение скоростей их расселения. Хаффейкер предположил, что, облегчив передвижение жертвы и затруднив передвижение хищника, можно увеличить время их сосуществования. Для этого на подносе из 120 лунок среди резиновых мячиков располагали случайным образом б апельсинов, причем вокруг лунок с апельсинами были устроены преграды из вазелина, препятствовавшие расселению хищника, а для облегчения расселения жертвы на подносе были укреплены деревянные колышки, служившие своего рода «взлетными площадками» для растительноядных клещей (дело в том, что этот вид выпускает тонкие нити и с помощью их может парить в воздухе, распространяясь по ветру). В таком усложненном местообитании хищник и жертва сосуществовали в течение 8 мес., продемонстрировав три полных цикла колебаний численности (рис. 49, б). Наиболее важные условия этого сосуществования следующие: гетерогенность местообитания (в смысле наличия в ней пригодных и непригодных для обитания жертвы участков), а также возможность миграции жертвы и хищника (с сохранением некоторого преимущества жертвы в скорости этого процесса). Иными словами, хищник может полностью истребить то или иное локальное скопление жертв, но часть особей жертвы успеет мигрировать и дать начало другим локальным скоплениям. До новых локальных скоплений хищник рано или поздно тоже доберется, но тем временем жертва успеет расселиться в другие места (в том числе и в те, где она обитала раньше, но потом была истреблена).

Нечто подобное тому, что наблюдал Хаффейкер в эксперименте, встречается и в природных условиях. Так, например, бабочка кактусовая огневка (Cactoblastis cactorum), завезенная в Австралию, значительно снизила численность кактуса опунции[46], но не уничтожила его полностью именно потому, что кактус успевает расселиться немного быстрее. Обычно эти бабочки откладывают яйца не на каждое попадающееся растение опунции, а на некоторые кусты, показавшиеся им в силу каких-то причин особо привлекательными. Вылупившиеся личинки при высокой плотности обычно полностью уничтожают свое кормовое растение, при этом много личинок гибнет, будучи не в состоянии расселиться на соседние кусты (если только они не расположены друг к другу ближе, чем на 2 м). В тех местах, где опунция истребляется полностью, перестает встречаться и огневка. Поэтому, когда через некоторое время сюда вновь проникает опунция, то в течение определенного периода она может произрастать без риска быть уничтоженной огневкой. Со временем, однако, огневка снова здесь появляется и, быстро размножаясь, уничтожает опунцию. Приведенный выше пример — еще одно свидетельство важности учета расселения и вообще динамики пространственного распределения популяции при изучении динамики ее численности. Фактически эти два процесса в ряде случаев должны рассматриваться вместе как две стороны одного процесса — движения численности в пространстве — времени.

Говоря о колебаниях хищник — жертва, нельзя не упомянуть и о циклических изменениях численности зайца и рыси в Канаде, прослеженных по материалам статистики заготовок пушнины компанией Гудзон-Бэй с конца XVIII вплоть до начала XX в. (рис. 50). Этот пример нередко рассматривался как классическая иллюстрация колебаний хищник — жертва[47], хотя на самом деле мы видим только следование роста численности популяции хищника (рыси) за ростом численности жертвы (зайца). Что же касается снижения численности зайцев после каждого подъема, то оно не могло объясняться только возросшим прессом хищников, а было связано с другими факторами, по-видимому, прежде всего нехваткой корма в зимний период. К такому выводу пришел, в частности, М. Джилпин (Gilpin, 1973), пытавшийся проверить, могут ли быть описаны эти данные классической моделью Лотки—Вольтерры. Результаты проверки показали, что удовлетворительного соответствия модели нет, но как ни странно, оно становилось лучше, если хищника и жертву меняли местами, т. е. трактовали рысь как «жертву», а зайца — как «хищника». Подобная ситуация нашла свое отражение и в шутливом названии статьи («Едят ли зайцы рысей?»), по сути своей очень серьезной и опубликованной в серьезном научном журнале.