1. Системы линейных алгебраических уравнений
Часть 1
1. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
1. 1. Основные понятия
Рассмотрим систему m линейных уравнений с n неизвестными:
Обозначим матрицу из коэффициентов А, матрицу – столбец из свободных членов В, матрицу – столбец из неизвестных Х. Используя понятие произве-дения матриц, систему (2. 1) можно кратко записать в матричной форме:
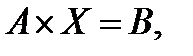 (1. 2)
(1. 2)
Определение 2. 1. Упорядоченный набор n чисел  называется решением системы (2. 1), если в результате замены неизвестных
называется решением системы (2. 1), если в результате замены неизвестных 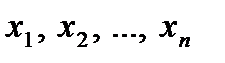 числами
числами  все уравнения системы превратятся в верные число-вые равенства.
все уравнения системы превратятся в верные число-вые равенства.
Определение 2. 2. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Определение 2. 3. Система (2. 1) называется однородной, если 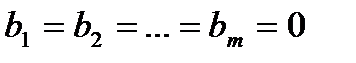 .
.
Очевидно, что однородная система всегда имеет тривиальное решение 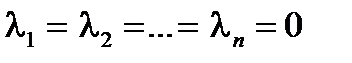 .
.
2. 2. Решение систем линейных уравнений с помощью обратной матрицы и по формулам Крамера
Рассмотрим систему
В матричной форме система имеет вид 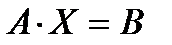 . Пусть
. Пусть 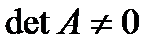 , сле-
, сле-
довательно, существует обратная матрица 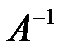 . Умножим левую и правую части
. Умножим левую и правую части 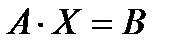 на
на 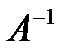 с левой стороны:
с левой стороны: 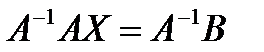 . Так как
. Так как 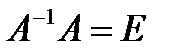 и
и 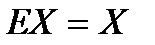 , то решение (2. 3) в матричной форме имеет вид
, то решение (2. 3) в матричной форме имеет вид
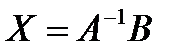 . (1. 4)
. (1. 4)
Для вывода формул Крамера ограничимся случаем n=3. Матричное равенство запишется в виде
Выражение 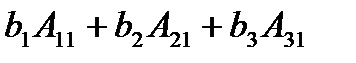 - разложение по первому столбцу определи-теля
- разложение по первому столбцу определи-теля
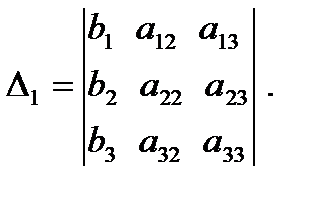
Аналогично
Следовательно, систему из n уравнений с n неизвестными с определи-телем из коэффициентов при неизвестных, отличным от нуля, можно решать по формулам, которые называются формулами Крамера:
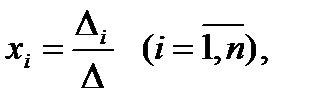 (1. 5)
(1. 5)
где ∆ - определитель из коэффициентов при неизвестных, 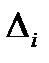 - определитель, полученный из ∆ заменой i-го столбца на столбец из свободных членов.
- определитель, полученный из ∆ заменой i-го столбца на столбец из свободных членов.
2. 3. Теорема Кронекера-Капелли
Первым вопросом, возникающем при изучении системы (1. 3), является вопрос о ее совместности. Ответ на него дает теорема Кронекера-Капелли (без доказательства).
Теорема 1. 1. Для совместности системы линейных алгебраических уравнений необходимо и достаточно, чтобы ранг матрицы А из коэффициентов при неизвестных был равен рангу расширенной матрицы 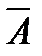 , под которой пони-мают матрицу А, дополненную столбцом свободных членов:
, под которой пони-мают матрицу А, дополненную столбцом свободных членов:
Приведем алгоритм решения системы из m уравнений с n неизвестными:
1. Находим rangA и rang 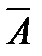 . Если они равны, то система совместна, если не равны – система не имеет решений.
. Если они равны, то система совместна, если не равны – система не имеет решений.
2. Если система совместна, выписываем равносильную систему, включа-ющую в себя только те уравнения, коэффициенты при неизвестных в которых образуют базисный минор.
3. Если система совместна и rang A=n, то систему можно решать по формулам Крамера или матричным способом. В этом случае система имеет единственное решение. Если rang A=r< n, то n-r членов, содержащих неизвестные с коэффициентами, не входящими в базисный минор, пе-реносим в правую часть. Эти неизвестные называются свободными пе-ременными и могут принимать любые значения. Неизвестные, остав-шиеся в левой части, называются главными (их r штук). Если rang A< n, то система имеет бесконечно много решений.
4. Решаем полученную систему r уравнений с r неизвестными по формулам Крамера или с помощью обратной матрицы.
Воспользуйтесь поиском по сайту:


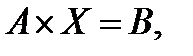 (1. 2)
(1. 2) называется решением системы (2. 1), если в результате замены неизвестных
называется решением системы (2. 1), если в результате замены неизвестных 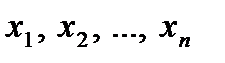 числами
числами  все уравнения системы превратятся в верные число-вые равенства.
все уравнения системы превратятся в верные число-вые равенства. 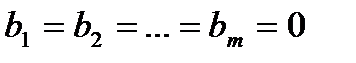 .
. 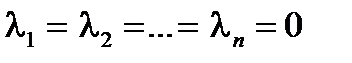 .
. 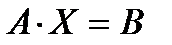 . Пусть
. Пусть 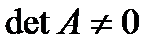 , сле-
, сле-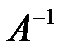 . Умножим левую и правую части
. Умножим левую и правую части 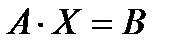 на
на 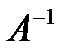 с левой стороны:
с левой стороны: 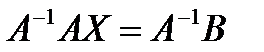 . Так как
. Так как 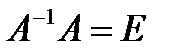 и
и 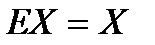 , то решение (2. 3) в матричной форме имеет вид
, то решение (2. 3) в матричной форме имеет вид 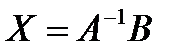 . (1. 4)
. (1. 4)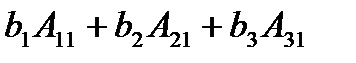 - разложение по первому столбцу определи-теля
- разложение по первому столбцу определи-теля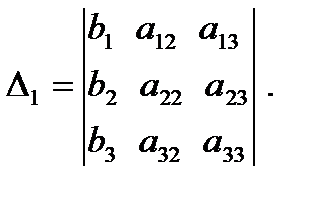
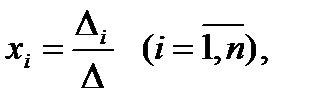 (1. 5)
(1. 5)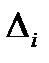 - определитель, полученный из ∆ заменой i-го столбца на столбец из свободных членов.
- определитель, полученный из ∆ заменой i-го столбца на столбец из свободных членов. 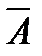 , под которой пони-мают матрицу А, дополненную столбцом свободных членов:
, под которой пони-мают матрицу А, дополненную столбцом свободных членов: 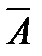 . Если они равны, то система совместна, если не равны – система не имеет решений.
. Если они равны, то система совместна, если не равны – система не имеет решений. 

