 |
Приложение 4. Комплексные числа. Список литературы
|
|
|
|
Приложение 4
КОМПЛЕКСНЫЕ ЧИСЛА
Здесь идет повторение, а скорее первое знакомство студентов с комплексными числами в их традиционном представлении в курсе высшей математики, приобретении навыков над действиями комплексных чисел, решении комплексных уравнений, что способствует лучшему усвоению материала по комплексному (символическому) методу расчета и анализа линейных электрических цепей переменного тока.
Комплексные числа — расширение множества вещественных чисел, обычно обозначается C. Любое комплексное число может быть представлено как формальная сумма x+iy, где x и y — вещественные числа, i — мнимая единица, то есть одно из чисел, удовлетворяющих уравнению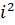 
=− 1. Общепринятым произношением является компле́ ксное число́ , что позволяет различить математический смысл слова комплексный и бытовой.
Комплексные числа образуют алгебраически замкнутое поле и являются частным случаем гиперкомплексных чисел.
Итак. комплексным числом 
называется арифметическое выражение вида
 ,
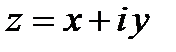| (4. 1) |
где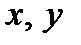 
- действительные числа, а 
- специальный символ, который называется мнимой единицей. Для мнимой единицы по определению считается, что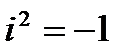 
.
(4. 1) – алгебраическая форма комплексного числа, причем 
называется действительной частью комплексного числа, а 
- мнимой частью.
Число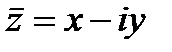 
называется комплексно сопряженным к числу .
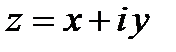Пусть даны два комплексных числа 
, 
.
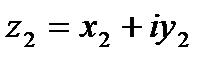1. Суммой 
комплексных чисел 
и 
называется комплексное число
.
2. Разностью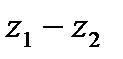 
комплексных чисел и называется комплексное число
.
3. Произведением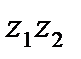 
комплексных чисел и называется комплексное число
.
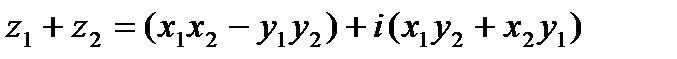4. Частным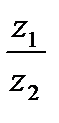 
от деления комплексного числа на комплексное число 
называется комплексное число
|
|
|
.
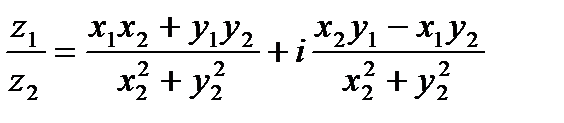Замечание 4. 1. То есть операции над комплексными числами вводятся по обычным правилам арифметических операций над буквенными выражениями в алгебре.
Пример 4. 1. Даны комплексные числа 
. Найти
.
Решение. 1) 
.
2) 
.
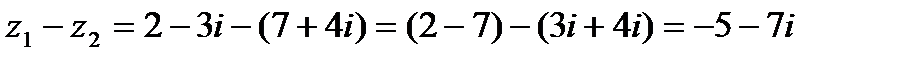3) 
.
4) Домножая числитель и знаменатель на комплексно сопряженное знаменателю число, получаем
.
Тригонометрическая форма комплексного числа:
,
где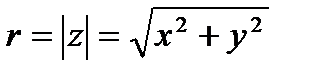 
- модуль комплексного числа, 
- аргумент комплексного числа. Угол 
определен неоднозначно, с точностью до слагаемого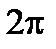 
:
, 
.
- главное значение аргумента, определяемое условием
, (или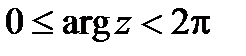 
).
Показательная форма комплексного числа:
.
Формула Муавра — формула, позволяющая возводить в степень комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:
= 
= 
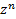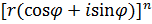(cos nφ + i sin nφ ) =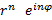 
где 
— модуль, а φ — аргумент комплексного числа.
Корень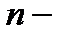 
й степени числа 
имеет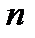 
различных значений, которые находятся по формуле
 ,
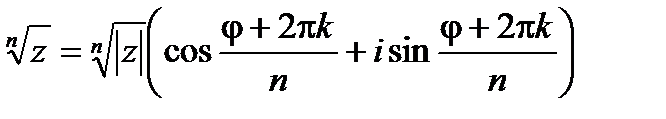| (4. 2) |
где 
.
Точки, соответствующие значениям 
, являются вершинами правильного 
угольника, вписанного в окружность радиуса 
с центром в начале координат.
Пример 4. 2. Найти все значения корня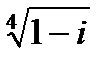 
.
Решение. Представим комплексное число 
в тригонометрической форме:
,
, откуда 
.
Тогда 
. Следовательно, по формуле (4. 2) 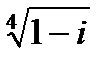имеет четыре значения:
, 
.
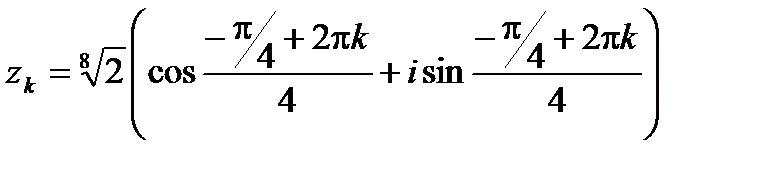Полагая 
, находим
, 
,
, 
.
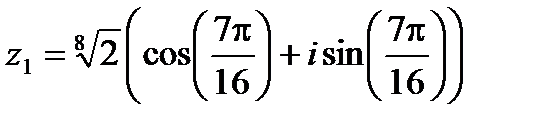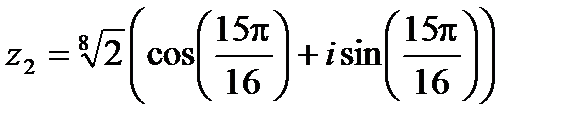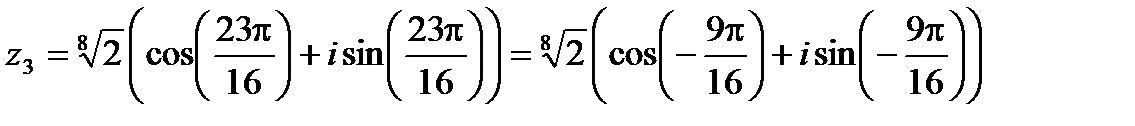Здесь мы преобразовывали значения аргумента к его главному значению.
Задача 1. Даны комплексные числа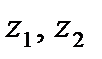 
. Найти .
1. 1.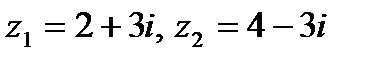 
| 1. 2.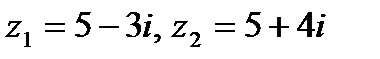 
|
1. 3. 
| 1. 4. 
|
1. 5. 
| 1. 6.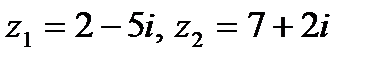 
|
1. 7.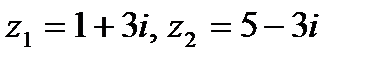 
| 1. 8. 
|
1. 9. 
| 1. 10. 
|
1. 11. 
| 1. 12.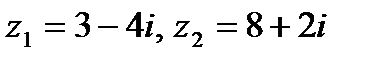 
|
1. 13. 
| 1. 14. 
|
1. 15.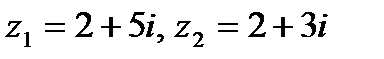 
| 1. 16. 
|
1. 17.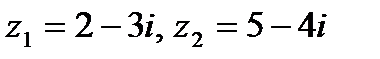 
| 1. 18. 
|
1. 19. 
| 1. 20. 
|
1. 21.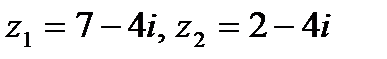 
| 1. 22. 
|
1. 23. 
| 1. 24. 
|
1. 25. 
| 1. 26.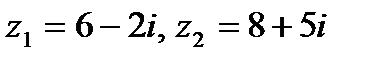 
|
1. 27.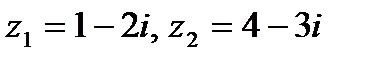 
| 1. 28.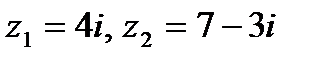 
|
1. 29.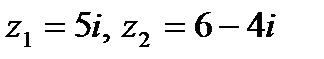 
| 1. 30. 
|
Задача 2. Найти все значения корня
2. 1.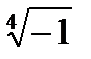 
| 2. 2.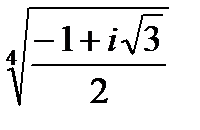 
|
2. 3. 
| 2. 4. 
|
2. 5. 
| 2. 6.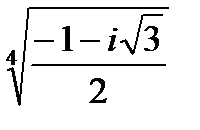 
|
2. 7. 
| 2. 8. 
|
2. 9.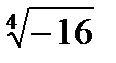 
| 2. 10. 
|
2. 11. 
| 2. 12.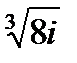 
|
2. 13. 
| 2. 14. 
|
2. 15. 
| 2. 16.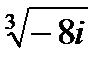 
|
2. 17.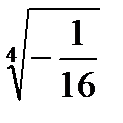 
| 2. 18. 
|
2. 19. 
| 2. 20.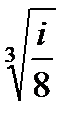 
|
2. 21. 
| 2. 22. 
|
2. 23.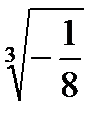 
| 2. 24. 
|
2. 25. 
| 2. 26. 
|
2. 27.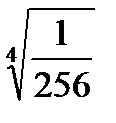 
| 2. 28. 
|
2. 29. 
| 2. 30.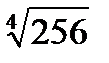 
|
|
|
|
СПИСОК ЛИТЕРАТУРЫ
1. Письменный Д. Т. Конспект лекций по высшей математике: полный курс / Д. Т. Письменный – М.: Айрис-пресс, 2004.
2. Бугров Я. С. Высшая математика. Элементы линейной алгебры и аналитической геометрии / Я. С. Бугров. С. М. Никольский. – М.: Наука, 1984.
3. Высшая математика в упражнениях и задачах: учеб. пособие для вузов / П. Е. Данко [и др. ] – 7изд., испр. – M.: ООО «Издательство Оникс»: ООО «Мир и Образование», 2008.
4. Кузнецов Л. А. Сборник заданий по высшей математике: типовые расчеты. / Л. А. Кузнецов – СПб.: Издательство «Лань», 2007.
5. Марон И. А. Дифференциальное и интегральное исчисление в примерах и задачах. Функции одной переменной / И. А. Марон – М.: Наука, 1970.
6. Лебедева А. В. Высшая математика: комплекс учебно-методических материалов. Ч. 1 / А. В. Лебедева, С. В. Решетняк. Нижегород. гос. техн. ун-т. Нижний Новгород, 2006.
7. Кольчик И. В. Высшая математика: комплекс учебно-методических материалов. Ч. 2 / И. В, Кольчик. Нижегород. гос. техн. ун-т. Нижний Новгород, 2007.
8. Демирчян К. С., Нейман Л. Р. и др. Теоретические основы электротехники. Т. 1. «Питер», 2003.
9. Теоретические основы электротехники. Основы теории линейных электрических цепей/ Под ред. П. А. Ионкина. М., 2008.
10. Шебес М. Р. Теория линейных электрических цепей а упражнениях и задачах. Издательство «Высшая школа». М., 1990.
11. Алтунин Б. Ю., Кралин А. А. и др. Теоретические основы электротехники. Часть 1, Учебное пособие. НГТУ., Н. Н., 2013.
12. Башев А. А., Кралин А. А. и др. Энергетическая электроника. Сборник задач. Часть 1, Учебное пособие. НГТУ., Н. Н., 2014.
13. Гольдфарб Н. И. Физика. Задачник, 10-11 классы. ДРОФА, М., 2010.
14. Фомина М. В. Решебник задач по физике. М., 2008.
|
|
|
