 |
Кафедра «Высшая математика и механика»
|
|
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение
высшего образования
«Санкт–Петербургский государственный университет
аэрокосмического приборостроения»
Кафедра «Высшая математика и механика»
Линейная алгебра и аналитическая геометрия
СБОРНИК ЗАДАНИЙ
Методические указания
по контрольным работам для студентов
заочного отделения
Санкт-Петербург
Одобрено на заседании кафедры «Высшая математика и механика»
протокол № 12 от 19 июня 2019 г.
Сборник содержит задачи контрольных работ по математическому анализу для студентов заочного отделения технических направлений, предусмотренные учебной программой в соответствии с ФГОС. Задания и методические указания могут быть использованы в курсе дисциплин всех направлений и специальностей ГУАП.
Составители:
доцент, канд. экон. наук, доцент Т. А. Черняк;
доцент, канд. тех. наук, доцент Е. В. Состина
доцент, канд. экон. наук В. П. Пушкина
Рецензент: доктор физ. -мат. наук, доц. А. О. Смирнов
© Санкт-Петербургский государственный университет
аэрокосмического приборостроения
Требования к оформлению контрольных работ
1. Контрольные работы следует выполнять в отдельной тетради. На обложке тетради необходимо указать: название института Университета; название кафедры; название и номер контрольной работы; название (номер) специальности; фамилию, имя, отчество и номер зачетной книжки студента.
2. На каждой странице следует оставить поля размером 4 см для оценки решения задач и методических указаний проверяющего работу.
|
|
|
3. Условия задач переписывать полностью необязательно, достаточно указать номера задач по данному сборнику. В условия задач следует сначала подставить конкретные числовые значения параметров т и п, после чего выполняется их решение.
4. Задачи в контрольной работе нужно располагать в порядке возрастания номеров.
Формирование исходных данных к задачам
Каждая контрольная работа состоит из задач одного или нескольких разделов сборника.
Условия задач, входящих в контрольную работу, одинаковы для всех студентов, однако числовые данные задач зависят от личного шифра студента, выполняющего работу.
Числовые значения параметров т и п определяются по двум последним цифрам номера зачетной книжки (А – предпоследняя цифра, В – последняя цифра). Значение параметра т выбирается из таблицы 1, а значение параметра п – из таблицы 2. Числа т и п следует подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра т)
| А | ||||||||||
| т |
Таблица 2 (выбор параметра п )
| В | ||||||||||
| п |
Например, если номер зачетной книжки 2018/ 5037, то А = 3, В = 7, и из таблиц находим, что т = 4, п = 2. Полученные т = 4 и п = 2 подставляются в условия всех задач контрольной работы студента.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Данко, П. Е. Высшая математика в упражнениях и задачах: учеб. Пособие: в 2 ч. / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. – М.: Оникс 21 век, 2005.
2. Лунгу К. Н., Норин В. П., Письменный Д. Т., Шевченко Ю. А. Сборник задач по высшей математике. 1 курс – М.: Айрис-пресс, 2009.
3. Лунгу К. Н., Норин В. П., Письменный Д. Т., Шевченко Ю. А. Сборник задач по высшей математике. 2 курс – М.: Айрис-пресс, 2009.
4. Письменный Д. Т. Конспект лекций по высшей математике: в 2 ч. Ч. 1 / Д. Т. Письменный. – М. : Айрис-пресс, 2003.
|
|
|
5. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. – СПб.: Лань, 2015.
6. Кряквин В. Д. Линейная алгебра в задачах и упражнениях. – СПб: Лань, 2016.
7. Смирнов А. О., Гусман Ю. А. Аналитическая геометрия. СПб, изд-во ГУАП, 2012
Контрольная работа № 1. Элементы линейной алгебры.
1. 1. Найти значение матричного многочлена 
, если 
, 
, 
.
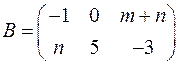1. 2. Вычислить определитель двумя способами, по правилу треугольника и разложением по строке (или столбцу): 
.
1. 3. Найти матрицу обратную к матрице 
и проверить выполнение равенства 
.
1. 4. Решить систему линейных алгебраических уравнений тремя способами: по формулам Крамера, с помощью обратной матрицы, методом Гаусса: 
.
1. 5. Даны комплексные числа 
и 
. Вычислить 
.
1. 6. Даны числа: 
, 
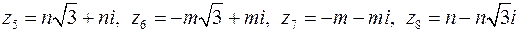. Изобразить числа на комплексной плоскости, найти модуль и аргумент, записать в тригонометрической и показательной форме.
1. 7. Даны числа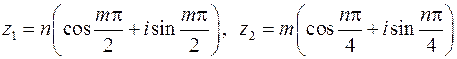 
. Вычислить 
.
|
|
|
