 |
1.7. Действия над комплексными числами в тригонометрической форме
|
|
|
|
Пример
Даны комплексные числа: 
, 
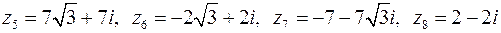. Изобразить числа на комплексной плоскости, найти модуль и аргумент, записать в тригонометрической и показательной форме.
Решение (рис. 2)
у
 |
7 z5
5, 5 z3
z6 2
z2 z1
-7 -5, 5 -3, 5 0 2 6 12, 1 х
-2 z8
-6
z4
z7 -12, 1
Рис. 2.
1. Найдем модуль и аргумент для комплексного числа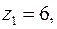 
. Подставляя модуль и аргумент в формулы (3) и (4), получим
.
2. Для 
имеем: 
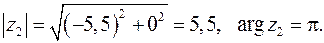
Следовательно:
.
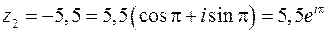3. Для 
имеем: 
Следовательно:
.
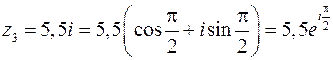4. Для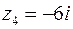 
имеем: 
Следовательно:
.
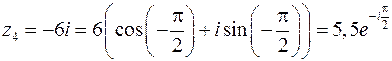5. Для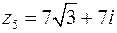 
имеем:
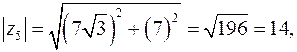
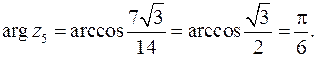
Следовательно:
.
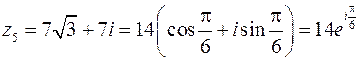6. Для 
имеем:
Следовательно:
.
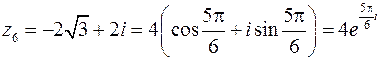7. Для 
имеем:
,
Следовательно:
.
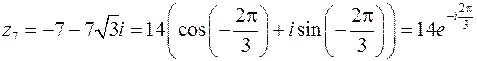8. Для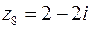 
имеем:
.
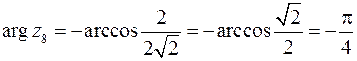Следовательно:
.
1. 7. Действия над комплексными числами в тригонометрической форме
Рассмотрим два комплексных числа в тригонометрической форме
и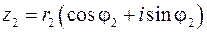 
.
При перемножении комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются, т. е.
|
|
|
.
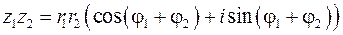Формула возведения комплексных чисел в натуральную степень:
.
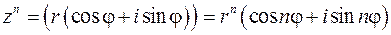Деление комплексных чисел, заданных в тригонометрической форме, выполняется по формуле
.
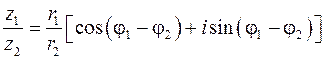Модуль частного равен частному от деления модуля числителя на модуль знаменателя, а аргумент частного равен разности аргументов делимого и делителя.
В результате умножения и деления чисел может получиться аргумент произведения и частного, не являющийся главным значением.
Пример
Даны числа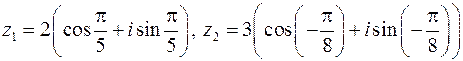 
.
Вычислить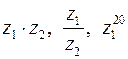 
.
Решение
Контрольная работа № 2. Элементы векторной алгебры и аналитической геометрии.
2. 1. Построить треугольник, вершины которого находятся в точках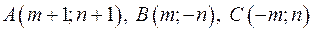 
и найти:
1) уравнение стороны АВ;
2) уравнение медианы, проведенной из вершины С;
3) координату точки пересечения медиан;
4) уравнение высоты, опущенной из вершины В на сторону АС и ее длину;
5) уравнение прямой, проходящей через точку С параллельно прямой АВ;
6) площадь треугольника.
2. 2. Даны вершины треугольной пирамиды 
, 
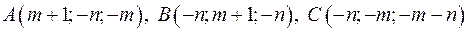. Найти:
1) угол между ребрам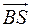и 
и 
;
2) площадь грани 
;
3) объем пирамиды 
;
4) длину высоты, опущенной из вершины S на грань АВС;
5) угол между ребром SC и гранью АВС;
6) уравнение высоты, опущенной из вершины S на грань АВС.
Краткие теоретические сведения для выполнения контрольной работы № 2 и решение типовых задач
2. 1. Прямая на плоскости
Уравнение вида
называется общим уравнением прямой.
Уравнение вида
называется уравнением прямой с угловым коэффициентов, здесь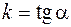 
, 
- угол, образованный прямой с положительным направлением оси Ох, b – ордината точки пересечения прямой с осью Оу.
Пусть даны две точки прямой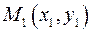 
и 
. Уравнение прямой, проходящей через две заданные точки имеет вид
.
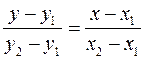Уравнение прямой, проходящей через заданную точку 
в заданном направлении, определяемом угловым коэффициентом k, имеет вид
|
|
|
.
Условие параллельности двух прямых
Две прямые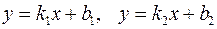 
параллельны в том и только в том случае, когда составляют равные углы 
с осью Ох, следовательно 
или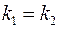 
.
Условие перпендикулярности двух прямых
Две прямые перпендикулярны в том и только в том случае, когда угол j между ними равен 
, т. е.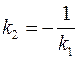 
.
Координаты точки 
, делящей отрезок АВ в данном отношении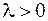 
, где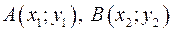 
, 
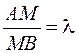, можно вычислить по формулам
.
В частности, если 
, то 
, т. е. М – середина отрезка АВ, то формулы примут вид
.
Если уравнение прямой дано в общей форме: , то расстояние точки 
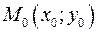до этой прямой находится по формуле:
.
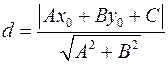Площадь треугольника с вершинами ,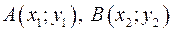 
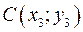можно вычислить по формуле
.
Пример
Даны вершины треугольника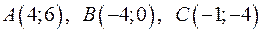 
. Найти:
1) уравнение стороны АВ;
2) уравнение медианы, проведенной из вершины С;
3) координату точки пересечения медиан;
4) уравнение высоты, опущенной из вершины В на сторону АС и ее длину;
5) уравнение прямой, проходящей через точку С параллельно прямой АВ;
6) площадь треугольника.
Решение
1) Используем уравнение прямой, проходящей через две точки 
. Подставив координаты точек 
, получим
- общее уравнение прямой АВ, из которого находим уравнение прямой с угловым коэффициентом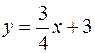 
, 
.
2) Медиана, проведенная из вершины С делит противолежащую сторону АВ треугольника пополам. Найдем координаты точки Е середины стороны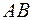 
(рис. 1):
, т. е. 
, 
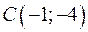. Подставим координаты точек в уравнение прямой, проходящей через две точки, получим 
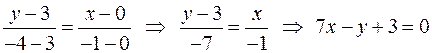- общее уравнение прямой СЕ.
3) Точка М делит каждую медиану в отношении 
, считая от вершины. Таким образом, ее координаты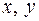 
можно найти по формулам:
.
В нашем случае
,
откуда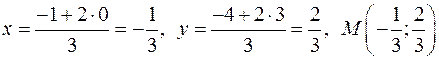 
.
4) Найдем уравнение прямой, проходящей через заданную точку 
перпендикулярно прямой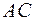 
из уравнения 
. Найдем угловой коэффициент прямой АС, используя уравнение прямой, проходящей через две точки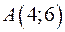 
и :
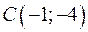- уравнение АС.
Угловой коэффициент прямой АС равен 
, тогда, используя условие перпендикулярности двух прямых 
, получим
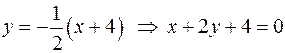- уравнение высоты.
Длину высоты можно найти, как расстояние от точки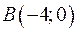 
до прямой АС по формуле 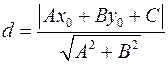. В нашем случае уравнение прямой АС: 
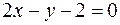, следовательно,
.
5) Для нахождения уравнения прямой, проходящей через точку С параллельно прямой АВ используем уравнение прямой, проходящей через заданную точку в заданном направлении 
и условие параллельности двух прямых. Известно, что угловой коэффициент прямой АВ равен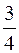 
, следовательно,
|
|
|
-
- уравнение искомой прямой.
6) Площадь треугольника находится по формуле: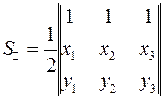 
, в нашем случае
.
у А(4; 6)
Е
В(-4; 0) М
0 1 х
С(-1; -4)
Рис. 1
|
|
|
