 |
1.5. Действия над комплексными числами
|
|
|
|
Пример 5
Исследовать и решить СЛАУр: 
.
Решение
~ 
~ 
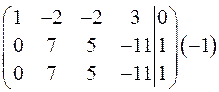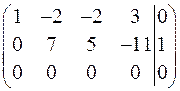
Так как 
, следовательно, система совместна и неопределенна (имеет бесчисленное множество решений).
Последней матрице соответствует система:
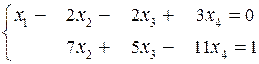Þ 
где 
и 
– произвольные параметры.
Пример 6
Исследовать и решить СЛАУр: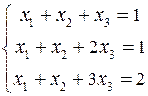 
Решение
~ 
~ 
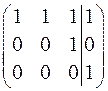
Так как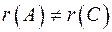 
, то система несовместна (решений нет).
Пример 7
Исследовать и решить СЛАУр: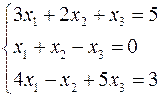 
.
Решение
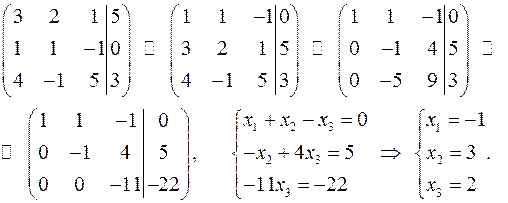
Таким образом, 
.
1. 5. Действия над комплексными числами
в алгебраической форме
Выражение вида
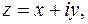(1)
где х и у – произвольные действительные числа, i – мнимая единица, удовлетворяющая условию 
, называется алгебраической формой записи комплексного числа.
Число х называется действительной частью комплексного числа z и обозначается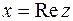 
, число у называется мнимой частью комплексного числа z и обозначается 
.
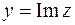При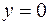 
число 
совпадает с вещественным числом х, если 
число 
называется чисто мнимым.
Два комплексных числа называются равными, если у них равны соответственно действительные и мнимые части:
.
Комплексные числа называются сопряженными, если у них равны действительные части, а мнимые противоположны по знаку; сопряженные числа обозначают
.
Определим основные действия над комплексными числами 
и 
, заданными в алгебраической форме.
Суммой двух комплексных чисел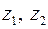 
называется комплексное число 
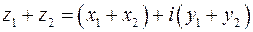, т. е. при сложении комплексных чисел складываются действительные и мнимые части соответственно.
|
|
|
Разностью комплексных чисел 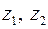называется комплексное число 
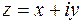, которое удовлетворяет равенству 
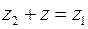. Очевидно: 
. При нахождении разности 
из действительной и мнимой частей уменьшаемого z1 вычитаются соответственно действительная и мнимая части вычитаемого z2.
Произведением комплексных чисел 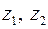называется комплексное число 
. Комплексные числа перемножаются как двучлены, при этом учитывается, что 
.
Частным от деления 
называется такое комплексное число z, которое удовлетворяет уравнению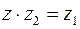 
. Для частного имеет место формула:
Чтобы разделить число z1 на z2 
, следует числитель и знаменатель дроби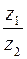 
умножить на число 
, сопряженное знаменателю.
Возведение комплексного числа z в степень n – это нахождение произведения n сомножителей, каждый из которых равен z, т. е.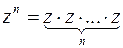 
. При возведении в степень n используется правило возведения в степень двучлена 
, в общем случае применяется формула бинома Ньютона.
Пример
Даны комплексные числа 
.
Вычислить 
.
Решение
,
,
,
,
,
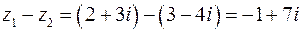1. 6. Тригонометрическая и показательная формы комплексного числа
Комплексное число 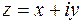изображается на плоскости Оху точкой М с координатами (х; у), либо вектором, начало которого находится в точке О(0; 0), а конец – в точке 
(рис. 1).
у=Im z
М(х, у)
r j
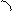
0 х=Re z
Рис. 1
Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, ось Ох – действительной осью, ось Оу – мнимой осью.
Число r – длина радиус-вектора точки 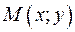(расстояние точки М от начала координат) называется модулем комплексного числа
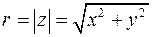. ( 2 )
|
|
|
Угол j, который образован вектором 
с осью Ох и отсчитываемый от положительного направления оси Ох, называется аргументом комплексного числа и обозначается Arg z.
Аргумент комплексного числа 
определен с точностью до слагаемого, кратного 
:
где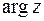 
– главное значение аргумента, определяемое условием
.
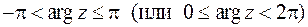Аргумент числа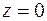 
неопределен.
Если вектор расположен в верхней полуплоскости, то угол j отсчитывается от положительного направления оси Ох против часовой стрелки до направления вектора , в данном случае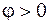 
.
Если вектор расположен в нижней полуплоскости, то угол j отсчитывается от положительного направления оси Ох по ходу часовой стрелки до направления вектора , в данном случае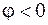 
.
Если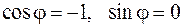 
, то будем считать, что 
.
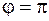Существует несколько подходов к определению аргумента. Один из них состоит в следующем. Если 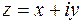, то аргумент
,
где .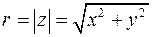
Учитывая, что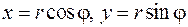 
, получим
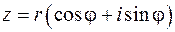- ( 3 )
тригонометрической форма записи комплексного числа.
Используя формулу Эйлера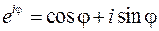 
, получим показательную форму комплексного числа:
, ( 4 )
где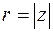 
– модуль, 
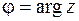– аргумент комплексного числа.
|
|
|
