 |
Пример 7. 1.3. Обратная матрица. 1.4. Решение систем линейных алгебраических уравнений. Матричный метод решения СЛАУр. Свойство 10. Сумма произведений элементов какого-нибудь столбца (или строки) на алгебраические дополнения элементов другого столбца (или
|
|
|
|
Пример 7
Вычислим определитель:
 ,
,
при вычислении определителя первую строку умножили на 2 и сложили со второй, затем разложили определитель по 2-й строке.
Свойство 10. Сумма произведений элементов какого-нибудь столбца (или строки) на алгебраические дополнения элементов другого столбца (или строки) определителя равна нулю.
1. 3. Обратная матрица
Пусть дана квадратная матрица А порядка n.
Обратной матрицей по отношению к данной А называется матрица  , которая будучи умноженной, как справа, так и слева на данную матрицу, дает единичную матрицу.
, которая будучи умноженной, как справа, так и слева на данную матрицу, дает единичную матрицу.
По определению
А ·  =
=  · А = Е.
· А = Е.
Квадратная матрица называется неособенной или невырожденной, если определитель ее отличен от нуля. В противном случае матрица называется особенной или вырожденной.
Всякая неособенная матрица имеет обратную матрицу, которую можно найти по формуле
 ,
,
где  - определитель матрицы А,
- определитель матрицы А, 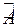 - союзная матрица по отношению к данной матрице, в которой элементы каждой строки данной матрицы заменены алгебраическими дополнениями элементов соответствующих столбцов. Например, для квадратной матрицы 2-го порядка союзной является матрица
- союзная матрица по отношению к данной матрице, в которой элементы каждой строки данной матрицы заменены алгебраическими дополнениями элементов соответствующих столбцов. Например, для квадратной матрицы 2-го порядка союзной является матрица
 ,
,
для квадратной матрицы 3-го порядка союзной является матрица
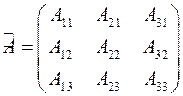 .
.
Пример
Для матрицы  найти обратную.
найти обратную.
Решение
Обратную матрицу находим по формуле
 .
.
Определитель матрицы 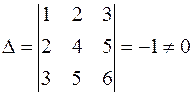 , следовательно, матрица неособенная и обратная матрица существует. Найдем алгебраические дополнения элементов матрицы:
, следовательно, матрица неособенная и обратная матрица существует. Найдем алгебраические дополнения элементов матрицы:



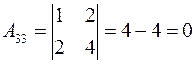 .
.
Тогда обратная матрица имеет вид
 .
.
1. 4. Решение систем линейных алгебраических уравнений
(СЛАУр)
Рассмотрим систему трех линейных уравнений с тремя неизвестными:
|
|
|
 . (1)
. (1)
Если хотя бы одно из чисел 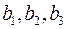 не равно нулю, то такая система называется неоднородной. Если же
не равно нулю, то такая система называется неоднородной. Если же 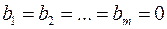 , то такая система называется однородной.
, то такая система называется однородной.
Решением системы (1) называется упорядоченная совокупность чисел  , которая при подстановке в систему обращает все уравнения системы в верные равенства.
, которая при подстановке в систему обращает все уравнения системы в верные равенства.
Если система имеет решение, то она называется совместной, если не имеет решения – то несовместной. Если система имеет единственное решение, то она называется определенной, если более одного решения, то – неопределенной.
Матричный метод решения СЛАУр
Запишем систему линейных уравнений в матричной форме. Введем обозначения:
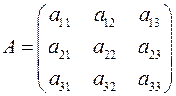 ,
,  ,
,  .
.
А – матрица коэффициентов системы,
Х – вектор-столбец неизвестных,
В – вектор-столбец свободных членов.
Тогда систему (1) можно кратко записать в матричной форме
 .
.
Умножим обе части равенства слева на матрицу  получим
получим
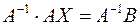 , но
, но 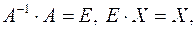
следовательно,
 .
.
Последняя формула дает решение системы (1) в матричной форме.
Пример 1
Решить систему 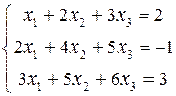 матричным методом.
матричным методом.
Решение
Матрица этой системы
 ,
,
обратная матрица имеет вид
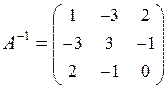
Применяя формулу  , получим
, получим
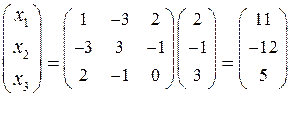
Следовательно,  ,
, 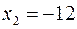 ,
,  .
.
Формулы Крамера для решения СЛАУр
Если определитель системы 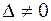 , то эта система имеет единственное решение, которое можно получить по формулам Крамера. Формулы Крамера имеют вид
, то эта система имеет единственное решение, которое можно получить по формулам Крамера. Формулы Крамера имеют вид
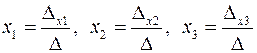 ,
,
где
 .
.
В знаменателях этих формул стоит определитель системы  , а в числителях – определители, которые получаются из определителя системы
, а в числителях – определители, которые получаются из определителя системы  заменой коэффициентов при соответствующих неизвестных столбцом свободных членов.
заменой коэффициентов при соответствующих неизвестных столбцом свободных членов.
Пример 2
Решить систему по формулам Крамера.
Решение
Формулы Крамера:  . Вычислим определители:
. Вычислим определители:
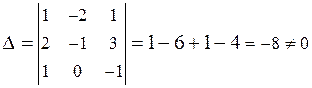 ,
,
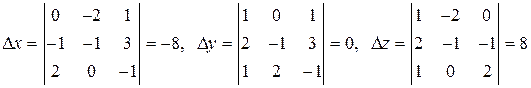 , тогда
, тогда
|
|
|
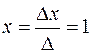 ,
,  ,
,  .
.
Итак,  ,
, 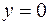 ,
,  .
.
|
|
|


