 |
4.4. Исследование шестизвенного рычажного механизма
|
|
|
|
4. 4. Исследование шестизвенного рычажного механизма
Далее рассмотрим пример структурного, кинематического и кинетостатического исследований шестизвенного механизма, представленного на рис. 4. 2.
|
| |
| а | |
| 
|
| б | в |
| Рис. 4. 2 | |
4. 5. Структурный анализ плоского рычажного шестизвенного механизма
Структурный анализ обязательно проводится перед кинематическим и динамическим. В данном пособии полностью изложен в разделе 2.
4. 6. Кинематическое исследование шестизвенного рычажного механизма
Задачи и методы кинематического исследования изложены в разделе (3. 1) данного пособия. Построение планов положений механизмов и построение траекторий описаны в разделах (3. 2) и (3. 3).
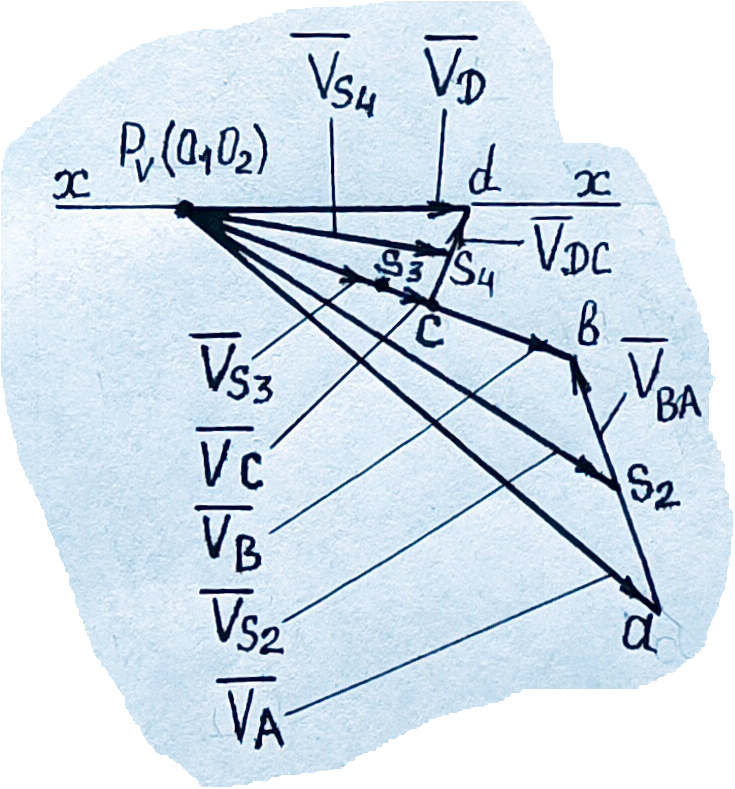
Кинематическое исследование, как и для рассмотренного уже четырехзвенного механизма, проводится в прямом порядке. Определяется скорость точки А кривошипа, записываются векторные уравнения для определения скорости точки В звена 2 и строится план скоростей (см. уравнения (3. 7) и (3. 8) и рис. 3. 1, б) в выбранном масштабе kv по формуле (3. 2).
Далее, воспользовавшись свойством подобия плана скоростей, определяется место нахождения точки С, составив арифметическую пропорцию:
(4. 24)
где длины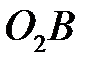 
и 
снимаются с чертежа схемы в мм, а длина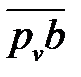 
– из плана скоростей, в мм.
Полученная точка С на плане скоростей отмечается стрелкой от полюса плана Рv. Вектор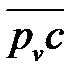 
– вектор скорости точки С механизма.
Определяем величину скорости точки D (ползуна) механизма. Точка D находится на звене 5 (ползуне), которое перемещается поступательно. Это движение на плане скоростей следует отметить горизонтальной (в данном примере) прямой х – х, проходящей через полюс плана Рv(О1О2) (cм. рис. 4. 2, б).
|
|
|
Кроме этого, точка D лежит и на звене 4 (CD – шатун). Ее движение следует рассматривать в зависимости от движения точки С, т. е. от относительной скорости VDC.
Представим скорость точки D в виде геометрической суммы переносной и относительной скоростей:
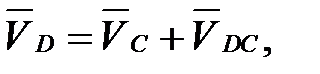(4. 25)
где 
– скорость точки С (известна по значению и направлению).
Из курса теоретической механики известно, что относительная скорость точки D во вращении вокруг точки С перпендикулярна к звену DC.
Точка С является «полюсом» для точки D. Из нее проводится вектор, перпендикулярно звену DC, до пересечения с линией хода ползуна х – х. На пересечении и будет находиться точка d. Вектор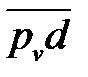 
– вектор скорости точки D механизма (рис. 4. 2, б).
Зная величину масштабного коэффициента kv плана скоростей, определяем значения скоростей всех точек механизма, умножая его на длины векторов в мм:
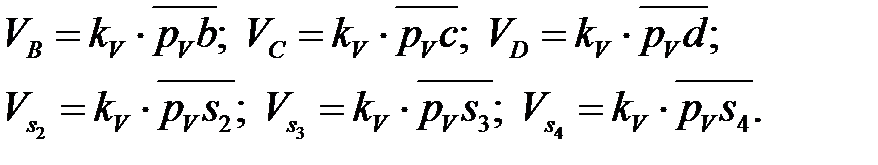(4. 26)
Точки s2, s3 и s4 находятся посередине соответствующих им звеньев АВ, ВО2 и DC. Это точки центров тяжести. Центр тяжести ползуна совпадает с точкой D (рис. 4. 2, б).
Для нахождения значений ускорений всех точек механизма следует построить план ускорений. Аналогично определению ускорений для четырехзвенного механизма (см. пункт 3. 5), пользуемся свойствами планов ускорений.
Начинаем построение плана с ведущего звена (кривошипа). Звено АО1 вращается равномерно, поэтому точка А имеет только нормальное (центростремительное) ускорение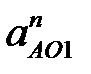 
, направленное по оси звена к центру вращения О1 (рис. 4. 2, в). Величину нормального ускорения вычисляем по формуле, м/с2:
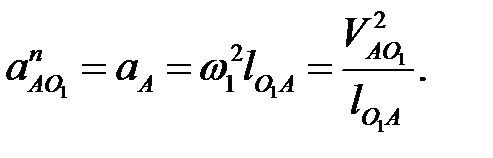(4. 27)
Длину отрезка, изображающего вектор ускорения 
, принимаем произвольно, в пределах 80 – 100 мм, и определяем масштабный коэффициент по формуле, м/с2× мм-1:
|
|
|
(4. 28)
Из полюса плана ускорений Ра параллельно звену АО1 в направлении от А к О1 откладываем вектор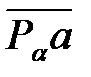 
(80 – 100 мм).
Затем составляем векторное уравнение для определения ускорения точки В, относящейся к двум звеньям (АВ и ВО2). На звене АВ точка В движется относительно точки А, а ее полное ускорение складывается из геометрической суммы нормального и тангенциального ускорений, так как в отличие от кривошипа АО1 звено АВ совершает сложное (плоскопараллельное) движение. «Полюсом» для точки В на звене АВ будет точка А; аналогичное пояснение относится и к точке В, когда рассматриваем ее движение на звене ВО2 и она движется относительно точки О2:
на звене АВ: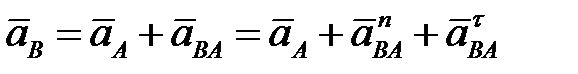 
(4. 29)
на звене ВО2: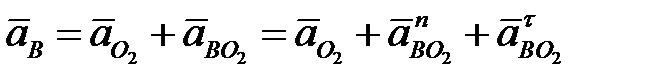 
(4. 30)
В этих уравнениях значения нормальных ускорений определяем аналогично формуле (4. 27); ускорение точки А известно по величине и по направлению, а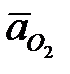 
= 0 (опора).
(4. 31) 
(4. 32)
Для построения плана ускорений следует определить с помощью масштаба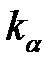 
длины отрезков, выражающих эти ускорения, мм:
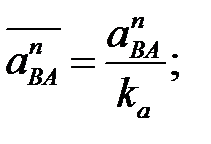(4. 33) 
(4. 34)
Далее выполняем построение: из точки а плана ускорений откладываем вектор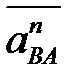 
параллельно звену АВ по направлению от В к А (см. звено! ). Через его конец проводим линию действия тангенциального 
перпендикулярно звену АВ (можно пунктиром). По аналогии строим 
из полюса Ра в сторону от В к О2 (см. звено! ), через его конец проводим линию действия тангенциального 
перпендикулярно звену ВО2 до пересечения с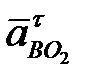 
. При пересечении получится точка В. Соединив точку В с полюсом Ра, получим вектор абсолютного ускорения точки В, а графически просуммировав 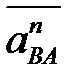и , получим вектор полного относительного ускорения 
(рис. 4. 2, в).
Находим места положений точек центров тяжести s2, s3, соединяем с полюсом Ра. Положение точки С на плане ускорений находим по свойству подобия (из пропорции):
(4. 35)
C помощью масштаба вычисляются значения ускорений точек группы Ассура АВО2 и точки С. Для этого длины векторов каждой точки следует умножить на величину коэффициента 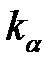(масштаба), м/с2:
|
|
|
| (4. 36) | 
| (4. 40) | |
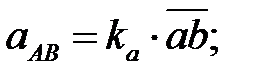
| (4. 37) |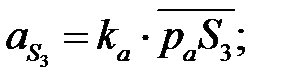 
| (4. 41) | |
| (4. 38) |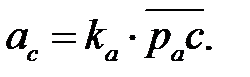 
| (4. 42) | |
| (4. 39) |
У шестизвенного механизма, как было ранее сказано, две группы Ассура: АВО2 и СD, присоединенная в точке С к группе АВО2.
Звено СD, как и звено АВ, совершает сложное движение. Точка D принадлежит звеньям 4 и 5. На звене СD точка D перемещается относительно точки С, ускорение которой известно (4. 42), а полное относительное ускорение 
состоит из геометрической суммы нормального и тангенциального ускорений. Векторное уравнение имеет вид:
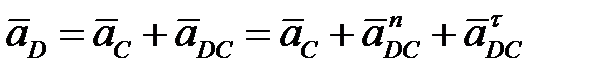(4. 43)
Аналогично формуле (4. 27), определим 
по величине:
(4. 44)
Для построения плана ускорений определяем длину вектора, выражающего это ускорение, мм:
(4. 45)
Из точки С плана параллельно звену DС в направлении от D к С (см. звено! ) откладываем вектор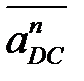 
. Из его конца пунктиром проводим линию действия тангенциального ускорения перпендикулярно звену DC до пересечения с линией хода х – х ползуна D (см. план ускорений). Точка пересечения обозначит точку d. Вектор 
направлен к точке d и обозначает абсолютное ускорение точки D. На середине отрезка cd находится точка s4, соединив которую с точкой полюса Ра, получим вектор ускорения центра тяжести звена CD.
С помощью масштаба находим значения ускорений звеньев и точек группы Ассура CD:
| (4. 46) |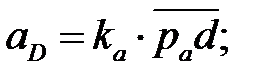 
| (4. 48) | |
| (4. 47) |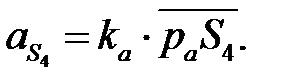 
| (4. 49) |
Определяем величину и направление углового ускорения звена CD. Известно, что угловое ускорение зависит и по величине, и по направлению от тангенциального, с-2:
(4. 50)
Для определения направления углового ускорения звена CD надо мысленно перенести вектор тангенциального ускорения в точку D звена CD. Точка D будет вращаться относительно точки C против часовой стрелки (рис. 4. 2, а). Ползун 5 совершает поступательное движение. Его угловое ускорение равно нулю.
|
|
|
|
|
|
