 |
4.7. Кинетостатическое исследование шестизвенного механизма
|
|
|
|
4. 7. Кинетостатическое исследование шестизвенного механизма
В разделе 4 данного пособия отмечено, что порядок силового расчета является обратным по сравнению с кинематическим, т. е. начинается с самой удаленной от ведущего звена группы Ассура.
Силовое исследование необходимо при проектировании новых механизмов, так как по найденным силам производится расчет на прочность кинематических пар и звеньев механизма.
Основными задачами силового расчета являются:
- определение сил, действующих на звенья;
- определение реакций в кинематических парах;
- определение уравновешивающей (движущей) силы или момента.
Ведется силовой расчет методом кинетостатики, т. е. наряду с внешними силами (движущими, веса звеньев, полезных и вредных сопротивлений) учитываются силы инерции масс звеньев.
В основе метода лежит принцип Даламбера: если ко всем внешним силам добавить силы инерции, то система считается находящейся в равновесии.
При кинетостатическом расчете механизм разбивается на группы Ассура, которые статически определимы. Необходимо последовательно рассмотреть условия равновесия отдельно каждой группы в том порядке, в каком определялся класс механизма, т. е. расчет начинается с группы Ассура, наиболее удаленной от ведущего звена. Ведущее звено рассчитывается последним.
Составляющие реакции (без учета сил трения) во вращательной паре направлены по звену (нормальная реакция) и перпендикулярно звену (тангенциальная реакция) и приложены в центре шарнира. При расчете необходимо определить их величины и направления. В поступательной паре известно, что направление реакций всегда перпендикулярно оси направляющих пары.
|
|
|
Определение реакций ведется методом плана сил. Рассмотрим на примере механизма, имеющего две группы Ассура, одна из которых имеет в составе ползун (рис. 4. 2, а).
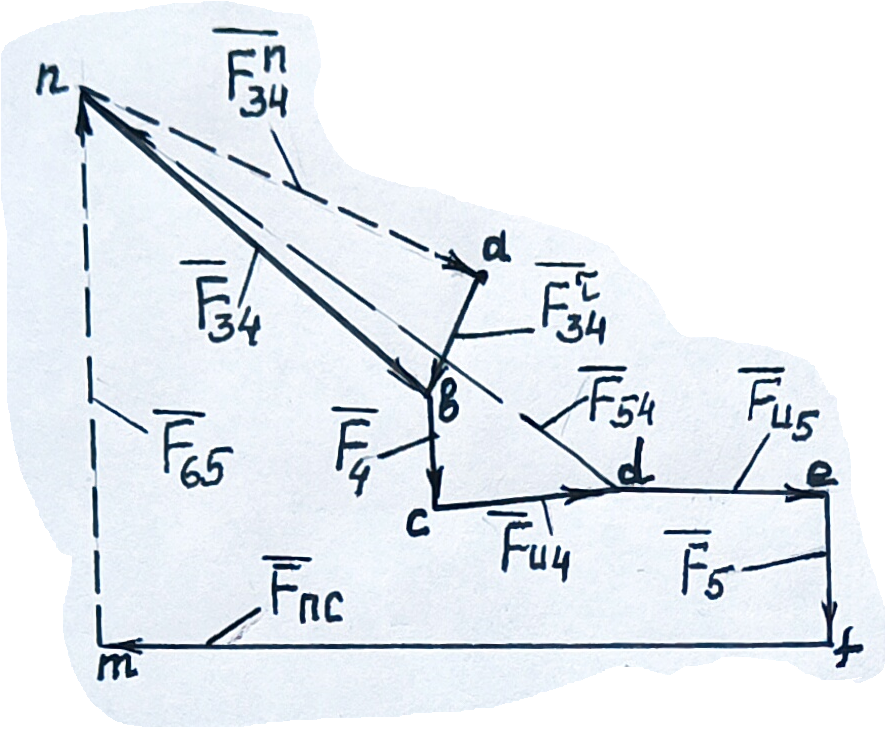
Вычерчиваем группу, состоящую из звеньев 4 и 5 в масштабе kl (схема вычерчена в этом масштабе), и прикладываем в соответствующих точках все силы, действующие на нее (рис. 4. 3, а)
|
| 
| |
| а | б | |
Рис. 4. 3
Для удобства, определение точек приложения, направлений и величин всех сил приведено в таблице 4. 1.
Таблица 4. 1
Определение точек приложения, величин и направлений сил,
действующих на группу Ассура CD
| Сила | Точка приложения | Направление силы | Величина силы определяется: |

| В центре | По звену CD | после построения плана сил |

| Перпендикулярно звену CD | из уравнения моментов сил относительно точки D | |

| В точке s4 центра тяжести звена CD (рис. 4. 3, а) | Противоположно ускорению 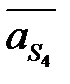 (рис. 4. 2, в) (рис. 4. 2, в)
|  , Н , Н
|

| В точке D ползуна 5 (рис. 4. 3, а) | Противоположно ускорению  ( (  ) (рис. 4. 2, в) ) (рис. 4. 2, в)
|  , Н , Н
|

| В точке s4 центра тяжести звена CD (рис. 4. 3, а) | Вертикально | 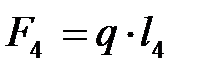 , Н где q – в задании; l – длина звена, мм , Н где q – в задании; l – длина звена, мм
|
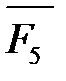
| В центре шарнира звена 5 | 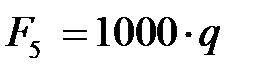 , Н где q – в задании , Н где q – в задании
| |
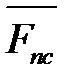
| Через центр шарнира D | Противоположно скорости  (рис. 4. 2, б) (рис. 4. 2, б)
|  , Н, задана в задании , Н, задана в задании
|

| Перпендикулярно линии x – x | после построения плана сил | |
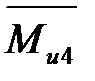
| К звену CD | Противоположно  (рис. 4. 3, а) (рис. 4. 3, а)
|  , где , где  , ,

|
Отсоединив группу CD от стойки 6 и звена 3, прикладываем вместо связей реакции  ,
,  и
и  (рис. 4. 3, а). Окончательные направления
(рис. 4. 3, а). Окончательные направления  и
и  определим из построенного плана сил, а
определим из построенного плана сил, а  – из уравнения моментов всех сил, действующих на звено CD, относительно точки D.
– из уравнения моментов всех сил, действующих на звено CD, относительно точки D.
Звено 4 (шатун) совершает плоскопараллельное (сложное) движение; при этом возникает сила инерции  , направлена противоположно ускорению
, направлена противоположно ускорению 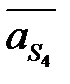 (рис. 4. 2, в) и приложена в точке s4. Противоположно угловому ускорению
(рис. 4. 2, в) и приложена в точке s4. Противоположно угловому ускорению  направлен момент инерции
направлен момент инерции 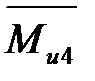 , представленный эквивалентной парой сил
, представленный эквивалентной парой сил  и
и 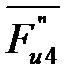 , приложенных в точках С и D в направлении действия момента
, приложенных в точках С и D в направлении действия момента 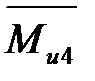 . Кроме этого, к звену 4 приложены сила тяжести
. Кроме этого, к звену 4 приложены сила тяжести  , реакции
, реакции  ,
,  (см. рис. 4. 3, а).
(см. рис. 4. 3, а).
|
|
|
Звено 5 (ползун) совершает поступательное движение вдоль неподвижной направляющей х – х; в этом случае возникает только сила инерции  , направленная противоположно ускорению
, направленная противоположно ускорению  . К ползуну приложена сила полезного сопротивления Fпс, направленная в сторону, противоположную скорости ползуна
. К ползуну приложена сила полезного сопротивления Fпс, направленная в сторону, противоположную скорости ползуна  и сила тяжести
и сила тяжести 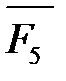 .
.
Составляем векторное уравнение равновесия всех сил, действующих на группу Ассура СD:
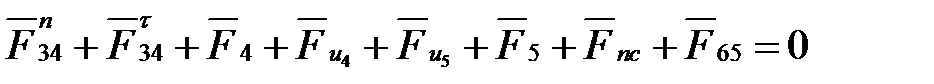 . (4. 51)
. (4. 51)
Чтобы группа находилась в равновесии, необходимо, чтобы многоугольник сил был замкнутым. При составлении уравнения рекомендуется вначале записать силы, действующие на звено 4, а затем на звено 5; неизвестные по величине реакции следует записать первыми и последними слагаемыми в уравнении (  ,
,  и
и  ).
).
Силы инерции  и
и 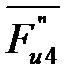 в уравнение не вписываются, так как они равны по величине, но противоположны по направлению.
в уравнение не вписываются, так как они равны по величине, но противоположны по направлению.
Определяем тангенциальную составляющую реакции в кинематической паре С (  ), составив уравнение моментов всех сил, действующих на звено CD, относительно точки D:
), составив уравнение моментов всех сил, действующих на звено CD, относительно точки D:
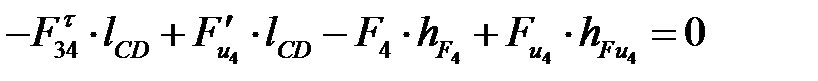 , (4. 52)
, (4. 52)
откуда
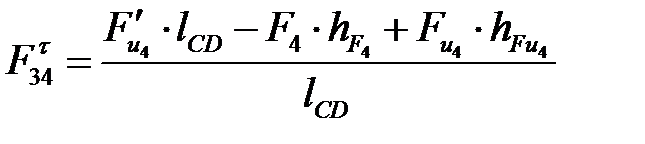 . (4. 53)
. (4. 53)
Длины 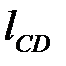 и плеч
и плеч  и
и  снимаются с чертежа группы Ассура в мм (рис. 4. 3, а). Если при определении реакция
снимаются с чертежа группы Ассура в мм (рис. 4. 3, а). Если при определении реакция  получится со знаком «плюс», то действительное направление на плане сил будет такое же, как на чертеже группы. Если со знаком «минус», то на плане сил вектор
получится со знаком «плюс», то действительное направление на плане сил будет такое же, как на чертеже группы. Если со знаком «минус», то на плане сил вектор  будет противоположно направлен (рекомендуется тонкой линией зачеркнуть существующий вектор и начертить нужный).
будет противоположно направлен (рекомендуется тонкой линией зачеркнуть существующий вектор и начертить нужный).
Графическое решение векторного уравнения равновесия (4. 51) называется планом сил.
4. 7. 1. Построение плана сил для определения реакций 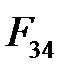 ,
,  и
и 
Выписав значения всех сил, действующих на звено CD и ползун, по максимальной из них определяем масштаб kF, разделив величину силы на длину вектора, которым она выражена на плане сил (принять произвольно, в пределах 100 – 180 мм):
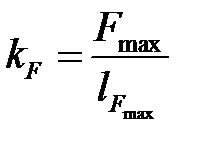 , Н/мм. (4. 54)
, Н/мм. (4. 54)
Затем с помощью масштаба определяем длины векторов всех сил, действующих на группу Ассура, мм:
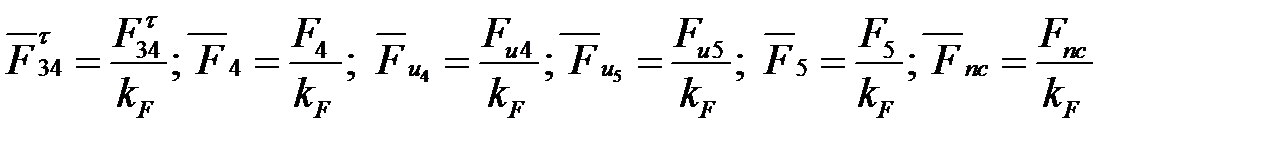
От точки а (рис. 4. 3, б) параллельно  на группе Ассура откладываем вектор
на группе Ассура откладываем вектор  , изображающий эту силу. Затем последовательно векторы остальных известных сил:
, изображающий эту силу. Затем последовательно векторы остальных известных сил: 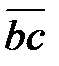 – сила тяжести
– сила тяжести  ;
; 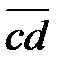 – сила инерции
– сила инерции  ;
; 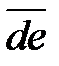 – сила инерции
– сила инерции  ;
;  – сила тяжести
– сила тяжести 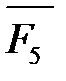 ;
; 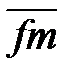 – сила полезного сопротивления
– сила полезного сопротивления 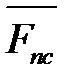 . Через точку m плана сил перпендикулярно направляющей хода ползуна – линию действия реакции
. Через точку m плана сил перпендикулярно направляющей хода ползуна – линию действия реакции  (пунктиром), а через точку а параллельно звену CD линию действия
(пунктиром), а через точку а параллельно звену CD линию действия  (тоже пунктиром). Точка n пересечения этих линий определит векторы
(тоже пунктиром). Точка n пересечения этих линий определит векторы  силы
силы  и
и 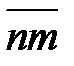 –
–  .
.
|
|
|
Вектор  – геометрическая сумма
– геометрическая сумма  и
и  , является полной реакцией
, является полной реакцией 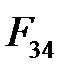 . Величины реакций
. Величины реакций  ,
,  и
и 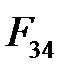 можно определить с помощью масштаба kF, Н:
можно определить с помощью масштаба kF, Н:
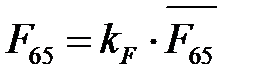 ;
; 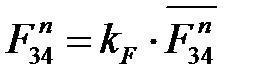 ;
;  . (4. 55)
. (4. 55)
Для определения реакции во вращательной паре D ( 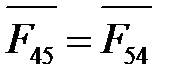 ) составим уравнение равновесия для одного звена CD (шатуна):
) составим уравнение равновесия для одного звена CD (шатуна):
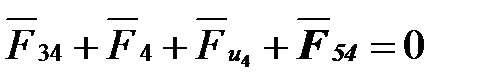 . (4. 56)
. (4. 56)
где  – реакция со стороны звена 5 на звено 4.
– реакция со стороны звена 5 на звено 4.
На плане сил векторы  ,
, 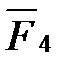 и
и  уже есть (рис. 4. 3, б), поэтому реакцией
уже есть (рис. 4. 3, б), поэтому реакцией  будет замыкающий вектор
будет замыкающий вектор  на этом же плане:
на этом же плане:
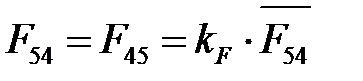 . (4. 57)
. (4. 57)
4. 7. 2. Построение плана сил для определения реакций  ,
,  и
и 
Определив реакции в кинематических парах самой удаленной группы Ассура CD, рассмотрим группу АВО2, к которой в точке С присоединена группа CD. Из плана сил этой группы определена реакция  в кинематической паре С. Звенья группы АВО2 находятся под действием сил, приведенных в таблице 4. 2.
в кинематической паре С. Звенья группы АВО2 находятся под действием сил, приведенных в таблице 4. 2.
Вычертив группу АВО2 в масштабе механизма kl и в том же положении, прикладываем все действующие на нее силы в соответствующих точках (см. рис. 4. 4, а и табл. 4. 2). Отсоединяем ее от стойки 6 и звена 1, заменив связи реакциями 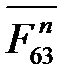 ,
,  ,
,  и
и  (рис. 4. 4, а). Окончательные направления
(рис. 4. 4, а). Окончательные направления 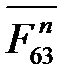 и
и  определятся из построенного плана сил, а
определятся из построенного плана сил, а  и
и  – из уравнений моментов всех сил, действующих на каждое звено в отдельности относительно точки В.
– из уравнений моментов всех сил, действующих на каждое звено в отдельности относительно точки В.
|
| 
| |
| а | б | |
Рис. 4. 4
Таблица 4. 2
Определение точек приложения, величин и направлений сил,
действующих на группу Ассура АВО2
| Сила | Точка приложения | Направление силы | Величина силы определяется: | ||
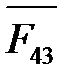
| В центре шарнира C |  (рис. 4. 4, а)
(рис. 4. 4, а)
| 
| ||

| В центре
| По звену О2В | после построения плана сил | ||

| Перпендикулярно звену О2В | из уравнения моментов сил относительно точки В | |||
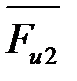
| В точке s2 центра тяжести звена АВ (рис. 4. 4, а) | Противоположно ускорению 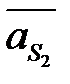 (рис. 4. 2, в) (рис. 4. 2, в)
| 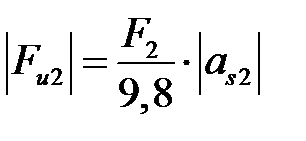 , Н , Н
| ||
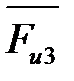
| В точке К (качания)

| Противоположно ускорению  (рис. 4. 2, в) (рис. 4. 2, в)
|  , Н , Н
| ||
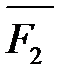
| В точке s2 центра тяжести звена AB (рис. 4. 4, а) | Вертикально вниз | 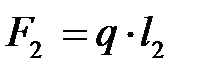 , Н где q – в задании; l – длина звена, мм , Н где q – в задании; l – длина звена, мм
|
Окончание таблицы 4. 2
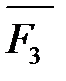
| В точке s3 центра тяжести звена ВО2 (рис. 4. 4, а) | Вертикально вниз |  , Н где q – в задании; l – длина звена, мм , Н где q – в задании; l – длина звена, мм
|

| Через центр шарнира A | По звену AВ | после построения плана сил |

| Перпендикулярно звену AВ | из уравнения моментов сил относительно точки В | |

| К звену AB | Противоположно  (рис. 4. 4, а) (рис. 4. 4, а)
|  , где , где 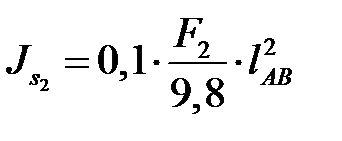 , ,
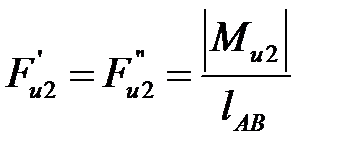
|
Звено 2 (шатун АВ) совершает сложное движение. Возникающая при этом сила инерции 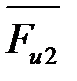 приложена в центре тяжести s2 и направлена противоположно ускорению
приложена в центре тяжести s2 и направлена противоположно ускорению 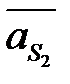 (рис. 4. 2, в и 4. 4, а). Момент инерции
(рис. 4. 2, в и 4. 4, а). Момент инерции  направлен противоположно угловому ускорению
направлен противоположно угловому ускорению  звена АВ. Этот момент представлен в виде эквивалентной пары сил
звена АВ. Этот момент представлен в виде эквивалентной пары сил  и
и  , приложенной в точках А и В. Плечом для них является длина звена АВ на чертеже группы Ассура АВО2. При этом круговое обозначение
, приложенной в точках А и В. Плечом для них является длина звена АВ на чертеже группы Ассура АВО2. При этом круговое обозначение  надо тонкой линией зачеркнуть, но не убирать на чертеже. Также к звену 2 приложены сила тяжести
надо тонкой линией зачеркнуть, но не убирать на чертеже. Также к звену 2 приложены сила тяжести 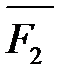 , реакции
, реакции  и
и  (рис. 4. 4, а).
(рис. 4. 4, а).
Звено 3 (коромысло ВО2) совершает неравномерное качательное движение вокруг опоры О2. На него тоже действует момент, который можно заменить парой сил инерции. Для удобства исследования принят другой, более простой вариант: силу инерции 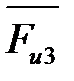 , направленную против ускорения центра тяжести
, направленную против ускорения центра тяжести  (рис. 4. 2, в), прикладываем в точке качания К, расположенную на расстоянии, мм:
(рис. 4. 2, в), прикладываем в точке качания К, расположенную на расстоянии, мм:
 , (4. 58)
, (4. 58)
где  – длина звена 3 на чертеже в мм.
– длина звена 3 на чертеже в мм.
Кроме этого, к звену 3 приложены сила тяжести 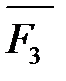 , реакции
, реакции  и
и  , и реакция
, и реакция 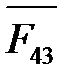 в точке С со стороны группы Ассура СD. По величине
в точке С со стороны группы Ассура СD. По величине  , но направлена в противоположную сторону, т. е.
, но направлена в противоположную сторону, т. е.  .
.
Составляем векторное уравнение равновесия всех сил, действующих на группу Ассура 2 – 3 (АВО2), учитывая указанные выше рекомендации:
 . (4. 59)
. (4. 59)
Определяем величину  , составив уравнение моментов всех сил, действующих на звено АВ относительно точки В:
, составив уравнение моментов всех сил, действующих на звено АВ относительно точки В:
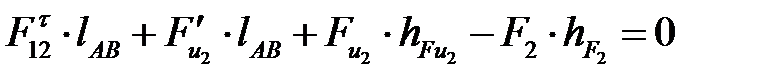 , (4. 60)
, (4. 60)
откуда
 . (4. 61)
. (4. 61)
Длины 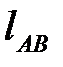 и плеч
и плеч 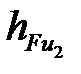 ,
, 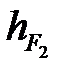 снимаются с чертежа группы Ассура в мм (рис. 4. 4, а).
снимаются с чертежа группы Ассура в мм (рис. 4. 4, а).
Для определения реакции 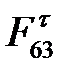 составляем уравнение моментов всех сил, действующих на звено ВО2 относительно точки В:
составляем уравнение моментов всех сил, действующих на звено ВО2 относительно точки В:
 , (4. 62)
, (4. 62)
откуда
|
|
|
 . (4. 63)
. (4. 63)
где длины 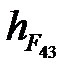 ,
, 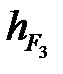 ,
, 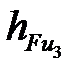 и
и  снимаем с чертежа группы Ассура (рис. 4. 4, а).
снимаем с чертежа группы Ассура (рис. 4. 4, а).
Если при определении  и
и 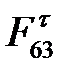 получится знак «плюс», то действительные направления этих реакций остаются такими же, как на группе Ассура. Если знак «минус», то следует перечеркнуть тонкой линией и начертить противоположное направление, и на плане сил чертить уже исправленное, согласно знакам.
получится знак «плюс», то действительные направления этих реакций остаются такими же, как на группе Ассура. Если знак «минус», то следует перечеркнуть тонкой линией и начертить противоположное направление, и на плане сил чертить уже исправленное, согласно знакам.
Выписываем значения всех сил, действующих на звенья группы АВ и ВО2. По максимальной силе определяем масштаб kF, разделив величину силы на длину вектора, которым выразим ее на чертеже плана сил (произвольно, в пределах 100 – 150 мм):
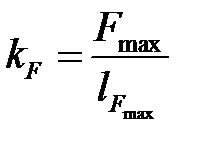 , Н/мм. (4. 64)
, Н/мм. (4. 64)
Масштаб может отличаться от предыдущего.
С помощью полученного масштаба определяем длины векторов всех сил, действующих на группу Ассура АВО2, мм:

Построение плана сил ведется по аналогии с построением плана для группы Ассура CD (рис. 4. 4, б).
Из точки а параллельно  на группе АВО2 откладываем вектор
на группе АВО2 откладываем вектор  , изображающий эту силу. Далее последовательно векторы всех остальных сил, известных по величине и направлению:
, изображающий эту силу. Далее последовательно векторы всех остальных сил, известных по величине и направлению: 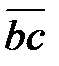 – сила инерции
– сила инерции 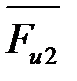 ;
; 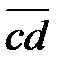 – сила тяжести
– сила тяжести  ;
; 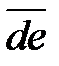 – сила инерции
– сила инерции  ;
;  – сила тяжести
– сила тяжести  ;
; 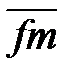 – реакция звена CD на звено ВО2
– реакция звена CD на звено ВО2  ;
; 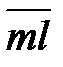 – сила
– сила 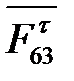 . Из точки l параллельно звену ВО2 пунктиром проводим линию действия нормальной составляющей реакции в кинематической паре О2
. Из точки l параллельно звену ВО2 пунктиром проводим линию действия нормальной составляющей реакции в кинематической паре О2  , а из точки а параллельно звену АВ –
, а из точки а параллельно звену АВ –  до пересечения с
до пересечения с  тоже пунктиром в точке n. Векторы
тоже пунктиром в точке n. Векторы 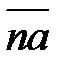 и
и 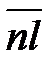 обозначают
обозначают  и
и  соответственно. Суммируя графически
соответственно. Суммируя графически  и
и  , получим полную реакцию в кинематической паре А (
, получим полную реакцию в кинематической паре А (  ), а вектор
), а вектор 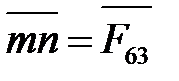 – реакцию в кинематической паре О2.
– реакцию в кинематической паре О2.
Для определения реакции в кинематической паре В ( 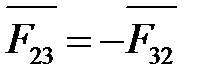 )составляем уравнение равновесия для одного из звеньев. Для звена АВ:
)составляем уравнение равновесия для одного из звеньев. Для звена АВ:
 . (4. 66)
. (4. 66)
где 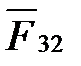 – реакция со стороны звена 3 на звено 2.
– реакция со стороны звена 3 на звено 2.
На плане сил векторы 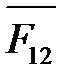 ,
, 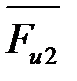 и
и  уже построены (рис. 4. 4, б), поэтому реакция
уже построены (рис. 4. 4, б), поэтому реакция 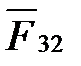 выражена замыкающим вектором
выражена замыкающим вектором 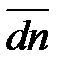 на этом же плане сил:
на этом же плане сил:
 . (4. 67)
. (4. 67)
4. 7. 3. Силовой расчет ведущего звена
В рассматриваемом примере передача энергии рабочему звену осуществляется кривошипом АО1 с учетом всех, действующих на него сил: веса (тяжести)  , инерции
, инерции  , реакции со стороны звена 2 (АВ)
, реакции со стороны звена 2 (АВ) 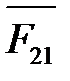 , равной
, равной 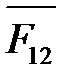 , но противоположно направленной. В точку А кривошипа приложена уравновешивающая (движущая) сила
, но противоположно направленной. В точку А кривошипа приложена уравновешивающая (движущая) сила  перпендикулярно к оси звена АО1 в направлении угловой скорости ꞷ 1. Требуется определить реакцию в кинематической паре О1 со стороны опоры на кривошип
перпендикулярно к оси звена АО1 в направлении угловой скорости ꞷ 1. Требуется определить реакцию в кинематической паре О1 со стороны опоры на кривошип  (рис. 4. 5, а).
(рис. 4. 5, а).
|
| 
| |
| а | б | |
Рис. 4. 5
Направления, точки приложения и величины сил, действующих на ведущее звено, сведены в таблицу 4. 3.
Таблица 4. 3
Определение точек приложения, величин и направлений сил,
действующих на ведущее звено О1А
| Сила | Точка приложения | Направление силы | Величина силы определяется: |

| В центре
| По направлению вращения (ꞷ 1) звена О1А | Из уравнения моментов сил относительно точки О1 |
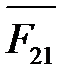
|  (рис. 4. 5, а)
(рис. 4. 5, а)
| 
| |

| В точке s1 центра тяжести звена О1А (рис. 4. 5, а)
| Вдоль звена О1А от точки О1 к точке А | 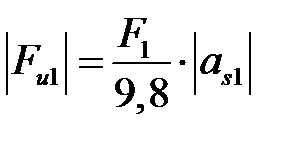 , Н , Н
|

| Вертикально вниз |  , Н где q – в задании; l – длина звена, мм , Н где q – в задании; l – длина звена, мм
| |

| В центре шарнира О1 | Из построенного плана сил | |
Определяем уравновешивающую силу (  ), составив уравнение моментов всех сил, действующих на кривошип, относительно точки О1:
), составив уравнение моментов всех сил, действующих на кривошип, относительно точки О1:
 , (4. 68)
, (4. 68)
откуда
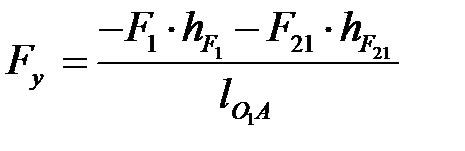 . (4. 69)
. (4. 69)
Длины плеч и длину кривошипа берем из чертежа (рис. 4. 5, а), мм.
Реакцию 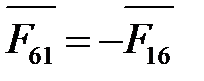 определяем, построив план сил согласно векторному уравнению равновесия:
определяем, построив план сил согласно векторному уравнению равновесия:
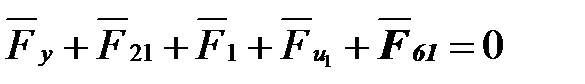 . (4. 70)
. (4. 70)
Масштаб определяем по максимальной силе, приняв длину ее вектора в пределах 50 – 80 мм:
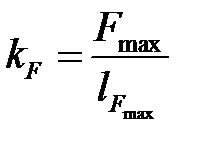 , Н/мм. (4. 71)
, Н/мм. (4. 71)
Замерив на плане сил длину замыкающего вектора  (рис. 4. 5, б), и умножив ее на масштабный коэффициент kF, получим численное значение реакции в опоре О1, Н:
(рис. 4. 5, б), и умножив ее на масштабный коэффициент kF, получим численное значение реакции в опоре О1, Н:
 . (4. 72)
. (4. 72)
Таким образом, в результате проведенных исследований и выполненных расчетов получены значения реакций в кинематических парах О1, А, В, С, D.
Зная реакции по величине и по направлению, можно рассчитать на прочность, жесткость и устойчивость механизм вцелом, задать форму сечений звеньев (круглые, овальные, из уголков и другие), если этого потребует заказчик, и, наконец, при необходимости усовершенствовать его.
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЩИТЕ ПЕРВРЙ ЧАСТИ
КУРСОВОЙ РАБОТЫ (ПРОЕКТА)
1) Каковы задачи структурного анализа механизма?
2) Что называется звеном, кинематической парой, механизмом, машиной?
3) Что такое структурная формула механизма и каков порядок ее составления?
4) Что такое группа Ассура? Объяснить ее формулу, класс, вид.
5) Написать формулу Чебышева. Пояснить составляющие, входящие в ее состав и физический смысл.
6) Перечислить методы построения траекторий точек звеньев. Что такое масштаб в ТММ?
7) Как определить масштаб плана скоростей механизма?
8) Пояснить построение плана скоростей механизма.
9) Пояснить построение плана ускорений механизма.
10) Перечислить свойства планов скоростей и ускорений. В чем сходство и разница планов скоростей и ускорений? Пояснить свойства подобия обоих планов.
11) Как вычисляются значения скоростей и ускорений центров тяжести звеньев?
12) Как определить угловые скорости и ускорения звеньев механизма по направлению и значению?
13) Как определить значения, направления, точки приложения сил инерции для разных звеньев?
14) Каков принцип построения векторных уравнений в силовом расчете?
15) Используя чертежи курсового проекта, определить значения сил в кинематических парах групп Ассура.
16) Какая сила называется уравновешивающей и как вычислить и определить ее по величине и направлению?
РАЗДЕЛЫ КУРСА ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ
1) Структурный анализ и классификация механизмов.
2) Кинематический анализ механизмов.
3) Силовой анализ механизма: силы, действующие на звенья; трение в механизмах; силы инерции.
4) Анализ движения механизмов и машин.
5) Синтез плоских зубчатых механизмов.
6) Синтез кулачковых механизмов.
Библиографический список
1. Артоболевский И. И. Теория механизмов и машин / И. И. Артоболевский. М.: Наука, 1988. 640 с.
2. Теория механизмов и машин. 3-е изд. / К. В. Фролов, С. А. Попов и др.; Под ред. К. В. Фролова. М.: Высшая школа, 2001. 496 с.
3. Курсовое проектирование по теории механизмов и машин.
Кореняко А. С. и др. М.: «Высшая школа», 1970, 332 с.
4. Структурный, кинематический и силовой анализ плоского рычажного механизма. Проектирование зубчатой передачи: методические указания к выполнению курсового проекта по дисциплине «Теория механизмов и машин» / Т. В. Вельгодская; Омский гос. ун-т путей сообщения. Омск, 2010, 51 с.
5. Рязанцева И. Л. Теория механизмов и машин в вопросах и ответах: Учебное пособие / И. Л. Рязанцева. – Омск: Изд-во ОмГТУ, 2013. – 132 с.
6. Смелягин А. И. Теория механизмов и машин. Курсовое проектирование: Учебное пособие. – М.: ИНФРА-М; Новосибирск: Изд-во НГТУ, 2003. – 263 с. – (Серия «Высшее образование»).
7. Сборник задач по теории механизмов и машин / Т. В. Вельгодская, Н. В. Ковалева, А. В. Бородин; Омский гос. ун-т путей сообщения. Омск, 2013. 75 с.
8. Проектирование механизмов и приборов. Заблонский К. И. и др. М.: «Высшая школа», 1971, 520 с.
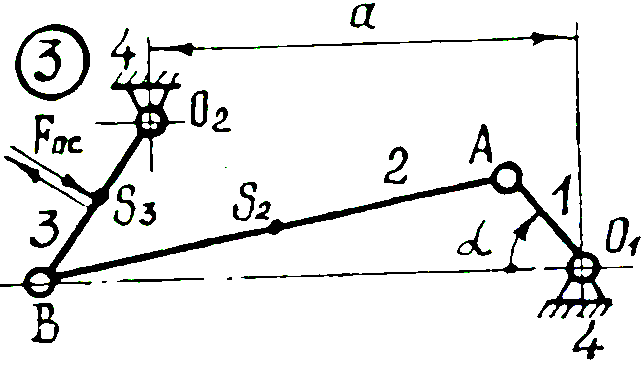
| Приложение 1. Схемы четырехзвенных механизмов для выполнения первой части курсовой работы (проекта) | ||
|
| ||

| 
| 
|

| 
|
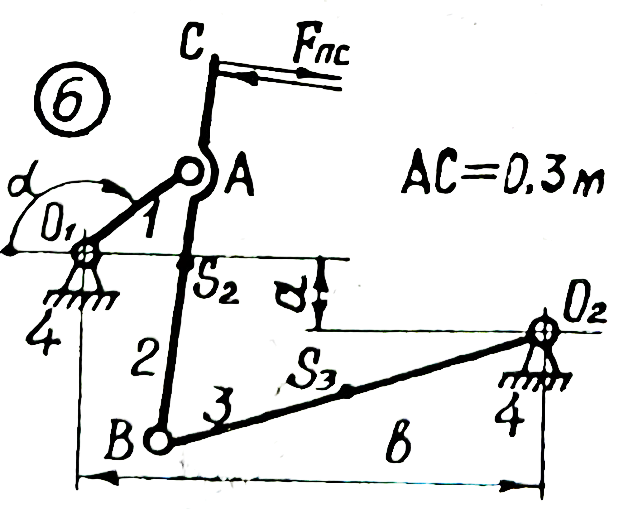
|
| Окончание приложения 1. | |

| 
|

|

|
ПРИЛОЖЕНИЕ 2
|
|
|





