3.3. Построение траекторий точек механизма

3. 3. Построение траекторий точек механизма

 

Для построения траектории какой-либо точки необходимо построить (на рис. 3. 1) несколько планов положений механизма (их 12), найти на каждом из планов положение заданной точки и соединить полученные точки последовательно плавной пунктирной линией. Траекторией кривошипа будет окружность радиуса О₁А, траекторией точки В – дуга радиуса О₂В, траекторией центра тяжести звена АВ (точка S₂) – вытянутая пунктирная замкнутая кривая.

 

3. 4. Определение скоростей точек механизма методом планов скоростей

 

Значения скоростей отдельных точек механизма необходимы при определении производительности и мощности машины, потерь на трение, кинетической энергии механизма, а также при расчете на прочность и при решении других динамических задач.

Зная закон движения ведущего звена и длину каждого звена механизма, можно определить скорости его точек по значению и направлению в любом положении механизма, построив план скоростей для этого положения.

Прежде чем строить план скоростей, следует изучить его свойства, так как они используются при построении:

1) векторы, проходящие через полюс плана P_V, выражают абсолютные скорости точек механизма и всегда направлены от полюса. В конце каждого вектора принято ставить строчную букву а, в, s, … или другую, которой обозначена точка на механизме (А, В, S, …) (см. рис. 3. 1, а, б). Точки плана скоростей, соответствующие неподвижным точкам механизма, находятся в полюсе плана Р_V (О₁, О₂);

2) векторы, соединяющие концы векторов абсолютных скоростей и не проходящие через полюс, изображают относительные скорости и всегда направлены к точке, обозначенной буквой, которая стоит первой в обозначении скорости. (Так как рассматривается движение точки В звена 2 относительно точки А, то и скорость V_ВА на плане направлена от точки а к точке в. Соответственно, на звене 3 скорость направлена к точке в, вектор  – к точке s₂ (рис. 3. 1, б);

3) на плане каждое подвижное звено изображается одноименным подобным контуром, повернутым относительно схемы механизма на 90°. Это свойство плана называется свойством подобия и позволяет (с помощью пропорции) легко находить место любой точки механизма на плане.

Кроме того, необходимо помнить о том, что относительная скорость при вращательном движении звена всегда направлена перпендикулярно к звену в сторону его угловой скорости, а при поступательном – по направлению движения (параллельно направляющей).

Построение плана скоростей начинают с определения угловой скорости кривошипа О₁А (см. рис. 3. 1, б) по формуле, 1/с:

 

(3. 4)

 

где n₁ - частота вращения кривошипа, об/мин.

Вычисляем скорость точки А кривошипа О₁А по формуле, м/с:

 

,                                                     (3. 5)

где  - длина кривошипа, м.

Из произвольной точки Р_V (полюс плана), в которой помещены и точки опор О₁ и О₂, откладываем перпендикулярно к звену О₁А в направлении вращения кривошипа отрезок 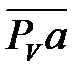 произвольной длины (рекомендуется длину отрезка  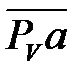принимать равной 80 – 100 мм, чтобы чертеж был четким).

Определяем масштаб плана скоростей, м/с·мм^–1:

 

                                                (3. 6)

 

Из курса теоретической механики известно, что скорость любой точки звена может быть представлена в виде геометрической суммы переносной и относительной скоростей. Воспользуемся векторными уравнениями для определения скорости точки В, когда она находится на втором и третьем звеньях:

 

                                      (3. 7)

 

                                        (3. 8)

где  - скорость точки А (известна по значению и направлению);

- относительная скорость точки В во вращении вокруг точки А (известна по линии действия, перпендикулярна к звену АВ);

 - скорость точки О₂, ;

 - относительная скорость точки В во вращении вокруг точки О₂ (известна по линии действия, перпендикулярна к звену ВО₂).

Для определения скорости точки В через точку а на плане скоростей проводим линию действия  перпендикулярно к звену механизма АВ, а через точку О₂ (в полюсе Р_V) - линию действия 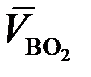 перпендикулярно к звену ВО₂. На пересечении этих двух линий действия получим точку в - конец вектора скорости  точки В механизма. Направление скорости точки В определяется вектором  (по первому свойству плана скоростей – от полюса к точке). Исходя из третьего свойства плана скоростей находим на плане точки s₂ и s₃, соответствующие центрам тяжести звеньев 2 и 3. Соединив эти точки с полюсом Р_V, получим векторы скоростей этих точек – и .

Пользуясь планом скоростей, вычисляем значения угловой скорости звеньев 2 и 3, с^–1:

 

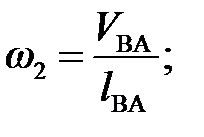               (3. 9)  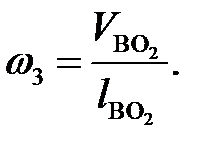                                (3. 10)

 

Для определения направления угловой скорости звена АВ вектор ско-рости , направленный к точке в плана, мысленно переносим в точку В звена АВ и видим, что вектор  стремится повернуть звено АВ вокруг точки А по ходу часовой стрелки. По аналогии определяем направление угловой скорости звена ВО₂ (по ходу часовой стрелки).

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: