 |
3.1. Задачи и методы кинематического исследования механизмов
|
|
|
|
3. 1. Задачи и методы кинематического исследования механизмов
В разделе 2 было показано, как любой механизм можно разложить на группы Ассура, каждая из которых при присоединении кинематическими парами к неподвижному звену обращается в статически определимую систему. Это позволяет развить методы кинематического и динамического исследования в применении не к механизму в целом, а к его отдельным частям, что удобно, так как можно обобщить методы исследования и сократить количество разновидностей механизмов для рассмотрения.
Основной задачей кинематики механизмов является изучение движения звеньев механизмов вне зависимости от сил, действующих на эти звенья, т. е. следует определить:
1) положение всех звеньев при любом мгновенном положении ведущего звена;
2) траекторию движения точек звеньев;
3) линейную скорость и ускорение точек звеньев;
4) угловую скорость и ускорения звеньев.
Существуют три основных метода кинематического исследования механизмов:
графиков (наименее трудоемкий и точный);
планов (более трудоемкий и точный);
аналитический (наиболее трудоемкий и точный).
В инженерных расчетах применяется графоаналитический метод, который дает удовлетворительную точность, но требует аккуратного выполнения графических работ и соблюдения масштаба.
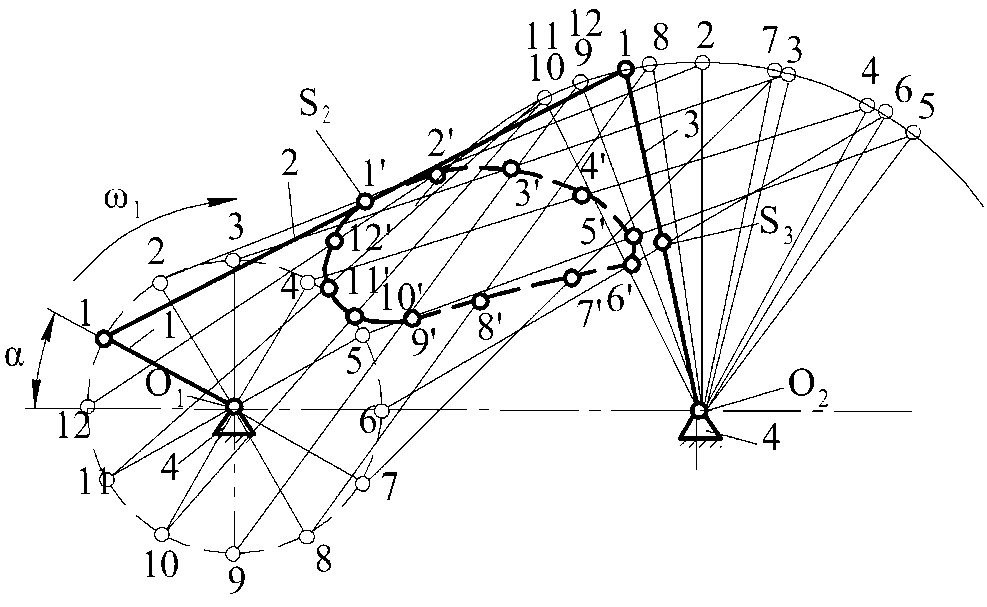
Под масштабом подразумевается определение масштабного коэффициента k (отношение действительной величины, выраженной в соответствующих единицах, к длине отрезка, изображающего эту величину, выраженную в миллиметрах). При построении кинематических схем и планов положений механизмов (рис. 3. 1, а) определяется масштабный коэффициент длины kl, показывающий число метров натуральной величины в одном миллиметре чертежа, м/мм:
|
|
|
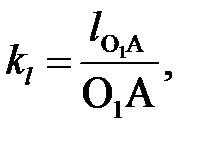
| (3. 1) |
где 
- действительная длина кривошипа, м
О1А - длина отрезка, изображающего кривошип на чертеже, мм.
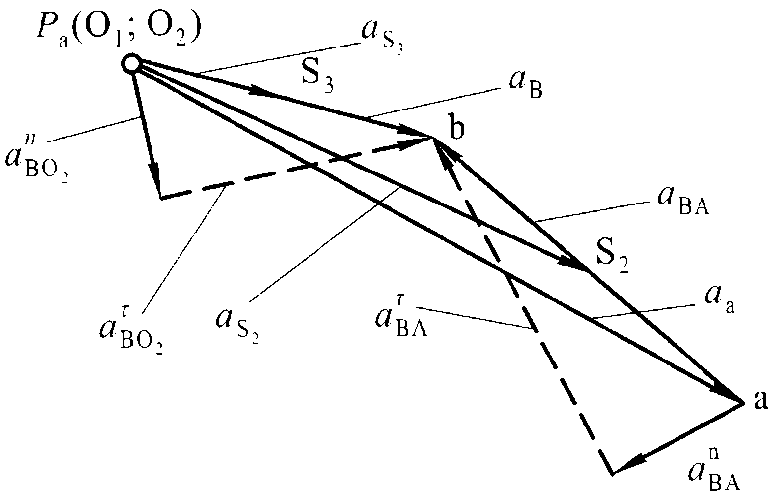
При построении планов скоростей и ускорений на чертеже приходится откладывать значения скорости и ускорения в некотором масштабе. Например, если вектор вычисленной скорости точки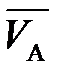 
, м/с, на плане скоростей изображен в виде отрезка 
произвольной длины, мм, (рис. 3. 1, б) то, поделив значение скорости VА на длину этого отрезка, найдем масштабный коэффициент плана скоростей, м/с·мм-1:
(3. 2)
Аналогично найдем масштабный коэффициент плана ускорений,
м/с2∙ мм-1 (рис. 3. 1, в):
(3. 3)
где аА - вычисленное значение ускорения точки А, м/с2;
- отрезок произвольной длины, соответствующий ускорению точки А на чертеже, мм.
а
| 
|
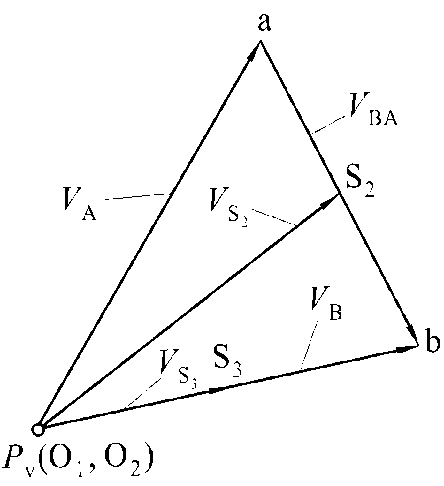
б в
Рис. 3. 1
Истинные значения скоростей и ускорений любых точек механизма получают путем умножения масштабных коэффициентов на длину соответствующих векторов.
3. 2. Построение планов положений механизмов
Планом положения механизма называется чертеж, изображающий расположение звеньев механизма в какой-то определенный момент движения (в зависимости от угла положения кривошипа α ).
Строятся планы положения механизма методом засечек.
Пример. Построить план положения механизма (см. рис. 3. 1, а) для заданного угла кривошипа α, равного 30°, если = 0, 200 м; lАВ = 0, 800 м;
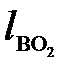= 0, 480 м; 
= 0, 640 м.
Решение. Принимаем, что длину кривошипа на схеме изображает отрезок О1А, длина которого равна 25 мм, тогда масштаб плана 
; 
м/мм.
Затем вычисляем значения длины других отрезков, изображающих звенья механизма на чертеже, мм:
|
|
|
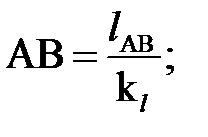
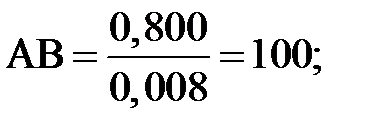
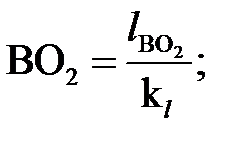
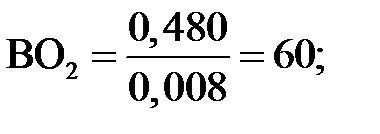
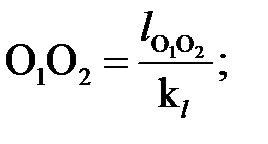
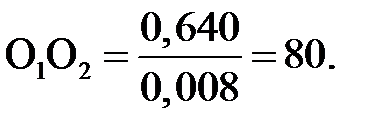
Построение плана положения механизма начинаем с нанесения элементов неподвижного звена (точек опор О1 и О2, а если есть ползун, то с нанесения линии хода ползуна). Под углом α = 30° из точки О1 откладываем отрезок О1А, равный длине кривошипа. Затем определяем положение точки В. Для этого из точки А проводим дугу радиусом АВ, а из точки О2 – дугу радиусом О2В. Точка пересечения дуг и будет точкой В (см. рис. 3. 1, а).
Рекомендуется при вычерчивании механизма длину отрезка, изображающего кривошип, принимать в пределах 25 – 40 мм.
|
|
|
