 |
1.4. Последовательность выполнения
|
|
|
|
1. 4. Последовательность выполнения
Задание состоит из двух частей. В первой части следует выполнить анализ и синтез плоского рычажного механизма:
1) вычертить схему механизма в заданном положении, выбрав масштабный коэффициент длины;
2) выполнить структурный анализ механизма;
3) построить планы положений механизма для восьми равноотстоящих друг от друга положений кривошипа;
4) начертить траектории всех точек механизма, в том числе и точек центров тяжести звеньев;
5) построить план скоростей для заданного положения механизма и определить с помощью масштабного коэффициента значения скоростей всех его точек;
6) определить значения угловых скоростей звеньев и указать их направления на схеме механизма;
7) построить план ускорений для заданного положения механизма и определить с помощью масштабного коэффициента значения ускорений всех его точек;
8) определить значения угловых ускорений звеньев и указать их направления на схеме механизма;
9) вычертить группу Ассура в том же положении и масштабе, как на схеме механизма;
10) определить значения и направления всех сил, действующих на звенья механизма, и приложить их в виде векторов на группе Ассура в соответствующих точках;
11) построить план сил группы Ассура и с помощью масштабного коэффициента сил определить реакции в кинематических парах;
12) выполнить расчет ведущего звена;
13) построить рычаг Жуковского (по указанию преподавателя).
Во второй части работы требуется выполнить геометрический расчет нулевой* цилиндрической прямозубой передачи с эвольвентным профилем зуба и определить (или проверить, если задано) передаточное отношение (число):
|
|
|
1) по данным расчета вычертить зацепление с контактом в полюсе зацепления (по три зуба на каждом колесе);
2) выделить активный участок линии зацепления и рабочие участки профилей зубьев обоих колес;
3) вычислить теоретическое значение коэффициента перекрытия;
4) по данным вычерченного зацепления определить значение действительного коэффициента перекрытия и сравнить его с теоретическим;
5) вычислить относительную ошибку, которая не должна превышать 5%**;
6) построить диаграмму коэффициентов относительного скольжения.
Внимание!
*) Преподаватель по желанию студента может предложить выполнить неравносмещенное зацепление, используемое в тяговых редукторах.
**) Если превышает 5%, объяснить возможную причину и способы изменения величины коэффициента перекрытия в обоих случаях.
2. СТРУКТУРНЫЙ АНАЛИЗ ПЛОСКИХ РЫЧАЖНЫХ МЕХАНИЗМОВ
Чтобы провести структурный анализ механизма, следует изучить его структуру.
2. 1. Структура механизма
2. 1. 1. Основные понятия и определения
Для облегчения труда человека и повышения его производительности создаются машины, механизмы, передачи [12].
Долгое время считалось, что машина – это устройство для выполнения механических движений. Но с развитием техники это понятие уточнялось, и сейчас оно несколько иное:
машина – это устройство для преобразования энергии, движения, материалов и информации для облегчения физического или умственного труда человека.
Для преобразования движения одного или нескольких элементов в требуемые движения других создается система элементов, которая называется механизмом.
Механизмы не совершают полезной работы, а только осуществляют требуемые законы движения их звеньев. Например, механические часы, пантографы, инверсоры и так далее.
2. 1. 2. Звенья механизма
Механизм состоит из отдельных элементов, называемых звеньями. Они могут быть твердыми (жесткими), упругими (пружины, мембраны), гибкими (цепи, ремни, канаты), жидкими (масло, вода). В данном пособии будут рассматриваться механизмы только с твердыми (жесткими) звеньями. Основные виды звеньев и их условные обозначения представлены в таблице 2. 1.
|
|
|
Звенья бывают неподвижные и подвижные. Неподвижные звенья – стойки. В станках это станины, в редукторах – корпус, в автомобилях – шасси или кузов. К стойке могут присоединить несколько звеньев, но в механизме она всегда одна. Подвижные звенья могут совершать вращательное, поступательное, сложное движение (см. табл. 2. 1).
Таблица 2. 1
Основные виды звеньев
| № п/п | Название | Условное обозначение | Движение | Особенности |
| Стойка | 
| Отсутствует | ||
| Стойка | 
| Отсутствует | ||
| Кривошип | 
| Вращательное | Полный оборот | |
| Шатун | 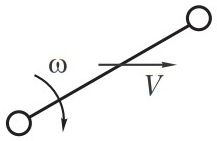
| Сложное | Нет пар, связанных со стойкой | |
| Коромысло | 
| Качательное | Неполный оборот | |
| Ползун | 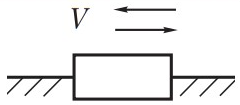
| Возвратно-поступательное | Направляющая неподвижна | |
| 1 Кулиса 2 Камень | 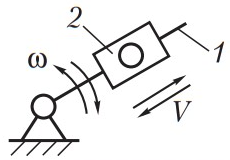
| Вращательное, колебательное | Направляющая подвижна | |
| 1 Кулиса 2 Камень | 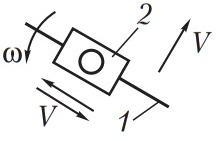
| Сложное | Направляющая подвижна |
Окончание таблицы 2. 1
| 1 Кулиса 2 Камень | 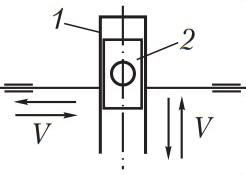
| Возвратно-поступательное | Направляющая подвижна | |
| 1 Шток 2 Качающийся ползун | 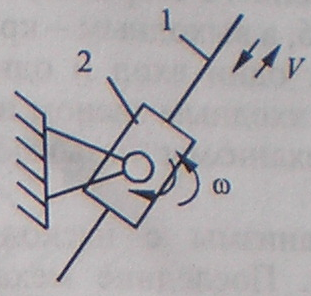
| Вращательное, колебательное и поступательное | Ползун вращается | |
| 1 Кулачок 2 Толкатель | 
| Вращательное, колебательное | Профиль определяет закон движения ведомого звена | |
| 1 Кулачок 2 Толкатель | 
| Возвратно-поступательное | Профиль определяет закон движения ведомого звена | |
| Зубчатое колесо | 
| Вращательное, качательное | Зубчатый контур | |
| Фрикционное колесо | 
| Вращательное, качательное | ||
| Рейка | 
| Возвратно-поступательное | Может иметь зубчатый контур |
2. 1. 3. Кинематические пары и их классификация
При конструировании машин необходима высокая точность их сборки и уменьшение сил трения в соединениях звеньев (в шарнирах, шаровых соединениях, поступательных движениях). Такие подвижные соединения двух звеньев называются кинематическими парами. В таблице 2. 2 приведены названия, условные обозначения и классификация кинематических пар.
|
|
|
Таблица 2. 2
Классификация кинематических пар
| № п/п | Рисунок | Название пары | Условное обозначение | Подвижность пары | Высшая или Низшая | Геометрическая или Силовая |

| Вращательная | 
| Н | Г | ||
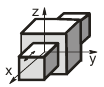
| Поступательная | 
| Н | Г | ||

| Винтовая | 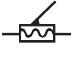
| Н | Г | ||
| Цилиндрическая | 
| Н | Г | ||

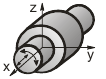
| Сферическая | 
| Н | Г С | ||

| Цилиндр-плоскость | 
| В | С | ||

| Шар-плоскость | 
| В | С |
Кинематические пары в зависимости от вида контактов звеньев могут быть высшими (когда элементы звеньев касаются в точке или по линии) и низшими (когда звенья соприкасаются по поверхности).
Чтобы звенья свободно двигались в местах соединений (в кинематических парах), они должны быть постоянно в контакте, то есть быть замкнутыми. Замыкание может быть силовым (массой, пружинами) или геометрическим (см. табл. 2. 2).
Примером механизма с низшими кинематическими парами может быть кривошипно-ползунный механизм, который является основным в поршневых машинах (двигателях внутреннего сгорания, компрессорах). Его конструкция и кинематическая схема приведены на рис. 2. 1, а, где звено
1 – кривошип, 2 – шатун, 3 – ползун, 4 – стойка (станина). Звено 1 соединяется со стойкой 4 вращательной кинематической парой I, звено 2 – со звеньями 1 и 3 – вращательными кинематическими парами II и III, а звено 3 (ползун) – со звеном 4 поступательной парой IV.

| 
|
| а | б |
Рис. 2. 1
Примером механизма с высшей кинематической парой является кулачковый механизм (рис. 2. 1, б). Форма кулачка 1 определяет закон движения толкателя 2. Кулачок 1 с толкателем 2 образуют высшую кинематическую пару (р4), кулачок 1 со стойкой 3 – низшую вращательную пару I, толкатель 2 со стойкой 3 – низшую поступательную пару II.
2. 1. 4. Кинематические цепи
Кинематической цепью называется связанная система звеньев, образующих между собой кинематические пары.
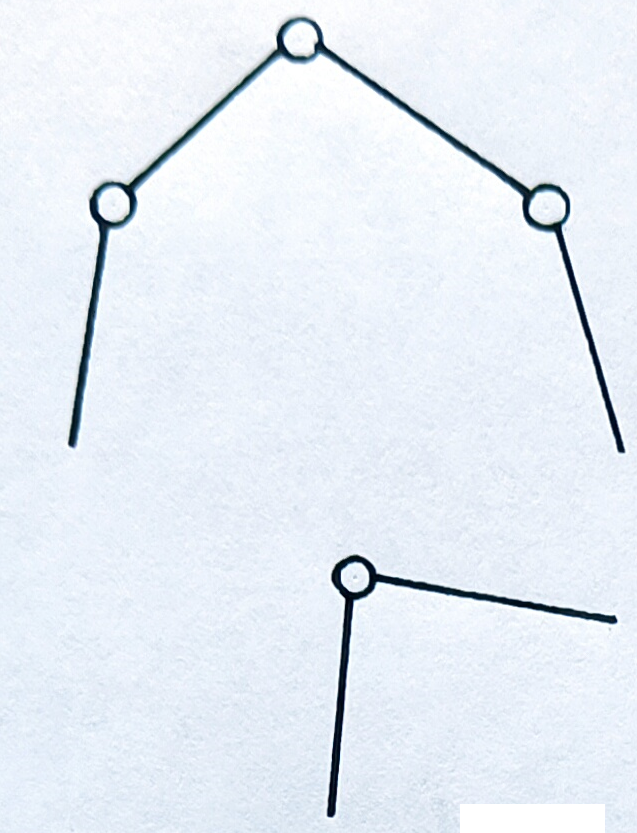
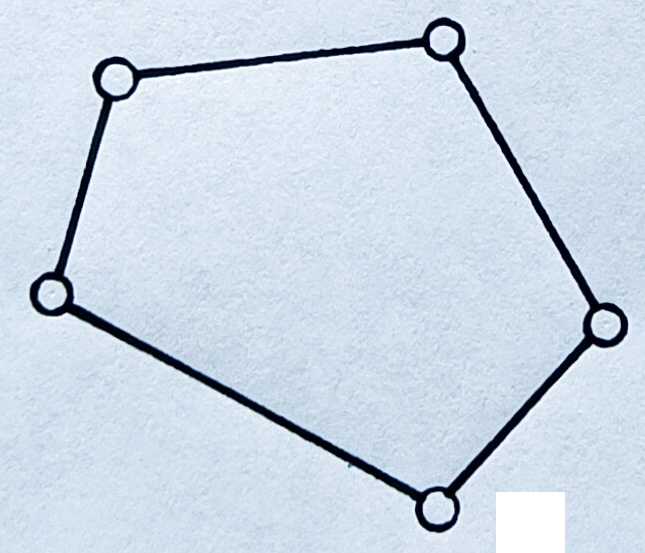
Кинематические цепи могут быть простыми и сложными. Простые – когда каждое звено входит не более, чем в две, кинематические пары (рис 2. 2, а, б). Сложные – в которых есть хотя бы одно звено, входящее более чем в две кинематические пары (рис. 2. 2, в, г). Простые и сложные кинематические цепи могут быть замкнутыми и незамкнутыми. Замкнутая – это такая цепь, у которой каждое звено входит хотя бы в две кинематические пары (рис. 2. 2, в, г). Незамкнутая – это когда есть звенья, входящие только в одну кинематическую пару (рис. 2. 2, а, б). И также надо отметить, что те и другие могут быть плоскими и пространственными.
|
|
|
| 
| 
| 
|
| а | б | в | г |
Рис. 2. 2
Таким образом, механизм – замкнутая кинематическая цепь, у которой при заданных законах движения ведущих звеньев остальные совершают определенные движения. Примеры механизмов см. на рис. 2. 1, а, б.
2. 1. 5. Структурная формула плоского механизма
В общем случае число степеней свободы механизма W может быть определено по структурной формуле Сомова – Малышева
| W = 6n - 5p5 - 4p4 - 3p3 - 2p2 - 1p1, | (2. 1) |
где n – количество подвижных звеньев;
p1 – p5 – количество кинематических пар соответственно индексу.
Если на движение всех звеньев наложено три ограничения, то число степеней свободы подвижных звеньев будет не 6n, а 3n: (6 – 3) n = 3n. Соответственно и вместо 5p5 связей, накладываемых парами пятого класса, в этом механизме пары пятого класса будут накладывать (5 – 3) p5 = 2p5 связей и так далее. Структурная формула будет такой:
W = (6 – 3)n - (5 – 3)p5 - (4 – 3)p4
то есть степень свободы плоского механизма будет равна:
W = 3n - 2p5 - 1p4; (2. 2)
В состав плоских механизмов пары первого, второго и третьего классов входить не могут, так как обладают пространственным характером относительных движений. А формула (2. 2) носит название формулы Чебышева. Ее физический смысл в том, что она определяет количество ведущих звеньев в механизме. То есть, если W = 1, то механизм будет работать, имея один двигатель (одно ведущее звено); если W = 2, то надо двум звеньям задать движение, чтобы остальные работали и так далее.
В формуле (2. 2) учтены только подвижные звенья (n). Если учитывать число звеньев, включая стойку, (k– общее число звеньев), то формула будет иметь вид:
W = 3k - 2p5 - 1p4 – 3*; (2. 3)
где 3* означает степень подвижности самой стойки, которая включена в 3k. Так как стойка не двигается, ее степень подвижности следует вычесть.
2. 1. 6. Основной принцип образования механизмов. Группы Ассура
Любой механизм должен иметь одно неподвижное звено – стойку, одно или несколько ведущих звеньев и кинематические цепи, подвижность каждой из которых (отдельно) равна нулю. Впервые этот принцип был сформулирован в 1914 году русским ученым Л. В. Ассуром.
|
|
|
Порядок присоединения групп звеньев с нулевой степенью подвижности следующий: первая группа присоединяется к ведущему звену и к стойке. Полученная схема механизма имеет подвижность, равную числу ведущих звеньев.
Для получения более сложных механизмов к звеньям присоединенной группы можно прикреплять такие же кинематические цепи с нулевой подвижностью. И опять степень подвижности полученного сложного механизма будет равна числу ведущих звеньев [4].
Кинематические цепи, имеющие нулевую подвижность, называются структурными группами или группами Ассура.
Класс группы определяется наивысшим классом контура, образуемого звеньями группы. Группы Ассура 2-го класса приведены на рис. 2. 3 а, б;
3-го класса – на рис. 2. 3 в, г.
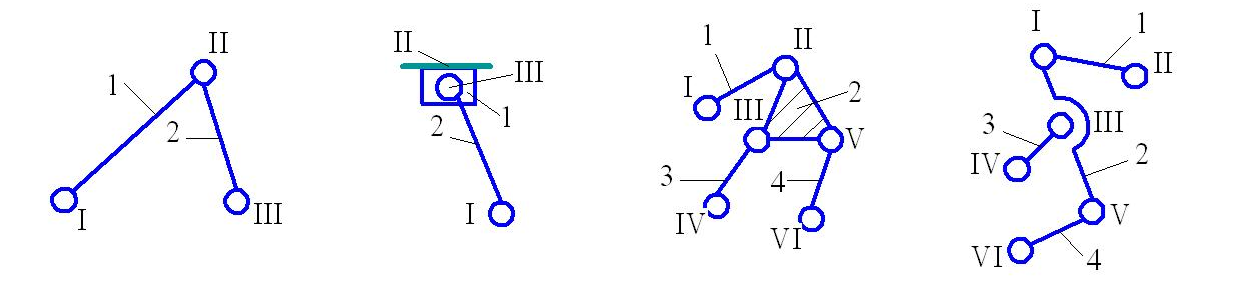
а б в г
Рис. 2. 3
Для определения класса механизма необходимо разделить его на группы Ассура, начиная с самой удаленной от ведущего звена группы 2-го класса, каждый раз проверяя степень подвижности оставшегося механизма, которая не должна изменяться, если отсоединение выполнено верно. Если подвижность изменилась или механизм распался, надо отсоединить группу более высокого класса, вновь проверить подвижность и так далее, пока не останется одно ведущее звено. По наивысшему классу групп Ассура определяется класс механизма.
Пример. Определить подвижность механизма, схема которого приведена на рис. 2. 4.
Воспользуемся формулой Чебышева:
W = 3n - 2p5 - 1p4;
при n = 9; p5 = 13; р4 = 0

Назначаем ведущим звено № 1.
Данный механизм разделяем на группы Ассура, начиная с самой удаленной от ведущего звена (см. рис. 2. 5).

| 
|
| Рис. 2. 4 | Рис. 2. 5 |
Таким образом, в состав механизма входят одно ведущее звено (1), двухповодковая группа Ассура 2-го класса (2, 3), трехповодковая группа 3-го класса (4, 5, 6, 7), двухповодковая группа 2-го класса (8, 9) (см. рис. 2. 6). Итак, имеем механизм третьего класса.
Структурная формула данного механизма записывается в порядке присоединения групп Ассура, начиная с ведущего звена:
[1]®[2; 3]®[4; 5; 6; 7]®[8; 9].
3. КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ ПЛОСКИХ
РЫЧАЖНЫХ МЕХАНИЗМОВ
|
|
|


