Оптимальная стратегия замены оборудования

 

Одной из важных экономических проблем является определение оптимальной стратегии в замене старых станков, агрегатов, машин на новые.

Старение оборудования включает его физический и моральный износ, в результате чего растут производственные затраты по выпуску продукции на старом оборудовании, увеличиваются затраты на его ремонт и обслуживание, снижаются производительность и ликвидная стоимость.

Наступает время, когда старое оборудование выгоднее продать, заменить новым, чем эксплуатировать ценой больших затрат; причем его можно заменить новым оборудованием того же вида или новым, более совершенным.

Оптимальная стратегия замены оборудования состоит в определении оптимальных сроков замены. Критерием оптимальности при этом может служить прибыль от эксплуатации оборудования, которую следует оптимизировать, или суммарные затраты на эксплуатацию в течение рассматриваемого промежутка времени, подлежащие минимизации.

Введем обозначения: r (t)— стоимость продукции, производимой за один год на единице оборудования возраста t лет;

u (t)— ежегодные затраты на обслуживание оборудования возраста t лет;

s (t) — остаточная стоимость оборудования возраста t лет;

Р — покупная цена оборудования.

Рассмотрим период N лет, в пределах которого требуется определить оптимальный цикл замены оборудования.

Обозначим через f_N (t) максимальный доход, получаемый от оборудования возраста t лет за оставшиеся N лет цикла использования оборудования при условии оптимальной стратегии.

Возраст оборудования отсчитывается в направлении течения процесса. Так, t =0 соответствует случаю использования нового оборудования. Временные же стадии процесса нумеруются в обратном направлении по отношению к ходу процесса. Так, N =1 относится к одной временной стадии, остающейся до завершения процесса, а N = N — к началу процесса.

На каждом этапе N -стадийного процесса должно быть принято решение о сохранении или замене оборудования. Выбранный вариант должен обеспечивать получение максимальной прибыли.

 

Возраст оборудования

0 1 2 3 t

Начало Конец

N N -1 1 0

Стадии

Рисунок 29

Функциональные уравнения, основанные на принципе оптимальности, имеют вид:

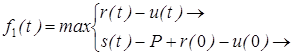
Уравнение описывает N -стадийный процесс, а — одностадийный. Оба уравнения состоят из двух частей: верхняя строка определяет доход, получаемый при сохранении оборудования; нижняя — доход, получаемый при замене оборудования и продолжении процесса работы на новом оборудовании.

В первом уравнении функция r(t) — u(t) есть разность между стоимостью произведенной продукции и эксплуатационными издержками на N- йстадии процесса.

Функция характеризует суммарную прибыль от (N — 1) оставшихся стадий для оборудования, возраст которого в начале осуществления этих стадий составляет (t + 1) лет.

Нижняя строка первого уравнения характеризуется следующим образом: функция s(t) — P представляет чистые издержки по замене оборудования, возраст которого t лет.

Функция r (0) выражает доход, получаемый от нового оборудования возраста 0 лет. Предполагается, что переход от работы на оборудовании возраста t лет к работе на новом оборудовании совершается мгновенно, т.е. период замены старого оборудования и переход на работу на новом оборудовании укладываются в одну и ту же стадию.

Последняя функция в первом уравнении представляет собой доход от оставшихся N— 1 стадий, до начала осуществления которых возраст оборудования составляет один год.

Аналогичная интерпретация может быть дана уравнению для одностадийного процесса. Здесь нет слагаемого вида , так как N принимает значение 1,2,..., N. Равенство = 0 следует из определения функции .

Указанные уравнения являются рекуррентными соотношениями, которые позволяют определить величину в зависимости от . Структура этих уравнений показывает, что при переходе от одной стадии процесса к следующей возраст оборудования увеличивается с t до (t + 1) лет, а число оставшихся стадий уменьшается с N до (N — 1).

Расчет начинают с использования первого уравнения. Данные уравнения позволяют оценить варианты замены и сохранения оборудования, с тем, чтобы принять тот из них, который предполагает больший доход. Эти соотношения дают возможность не только выбрать линию поведения при решении вопроса о сохранении или замене оборудования, но и определить прибыль, получаемую при принятии каждого из этих решений.

Пример 44. Определить оптимальный цикл замены оборудования при следующих исходных данных: Р = 10, s (t) = 0, f (t)= r (t) — u (t), представленных в таблице.

Таблица 24 - Исходные данные задачи.

N

f (t)

Решение. Уравнения запишем в следующем виде:

Для N =1 (для первой стадии развития)

Для N =2 (для второй стадии развития)

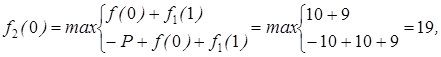
Вычисления продолжаем до тех пор, пока не будет выполнено условие > 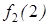, т.е. в данный момент оборудование необходимо заменить, так как величина прибыли, получаемая в результате замены оборудования, больше, чем в случае использования старого. Результаты расчетов помещаем в таблицу, момент замены отмечаем звездочкой, после чего дальнейшие вычисления по строчке прекращаем (табл. 25).

Можно не решать каждый раз уравнение, а вычисления проводить в таблице. Например, вычислим f ₄(t):

f ₄(0)= f ₁(0)+ f ₃(1)=10+24=34> f ₃(1)=24,

f ₄(1)= f ₁(1)+ f ₃(2)=9+21=30> f ₃(1),

f ₄(2)= f ₁(2)+ f ₃(3)=8+18=26> f ₃(1),

f ₄(3)= f ₁(3)+ f ₃(4)=7+17=24> f ₃(1),

f ₄(4)= f ₁(4)+ f ₃(5)=6+17=23> f ₃(1).

Дальнейшие расчеты для f ₄ (t)прекращаем, так как f ₄(4)=23 < f ₃(1) = 24.

По результатам вычислений и по линии, разграничивающей области решений сохранения и замены оборудования, находим оптимальный цикл замены оборудования. Для данной задачи он составляет 4 года.

Таблица 25 - Оформление задачи в виде таблицы.

 

 

FN(t)