 |
Шарнирная опора. Подвижный шарнир. Неподвижный шарнир. Защемление или «заделка». Примеры решения задач. Решение. Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, т
|
|
|
|
Шарнирная опора
Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.
Подвижный шарнир
Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки) (рис. 1. 10).
Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, т. к. не допускается только перемещение поперек опорной поверхности.
Неподвижный шарнир
Точка крепления перемещаться не может. Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Ее принято изображать в виде двух составляющих: горизонтальной и вертикальной ( Rx, Ry ) (рис. 1. 11).
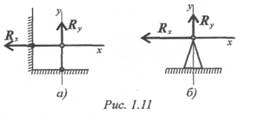
Защемление или «заделка»
Любые перемещения точки крепления невозможны.
Под действием внешних сил в опоре возникают реактивная сила и реактивный момент Mr, препятствующий повороту (рис. 1. 12).
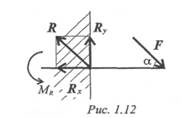Реактивную силу принято представлять в виде двух составляющих вдоль осей координат R = Rx + Ry.
10 Лекция 1
Примеры решения задач
Пример 1. Груз подвешен на стержнях и канатах и находится в равновесии (рис. 1. 13). Изобразить систему сил, действующих на шарнир А.
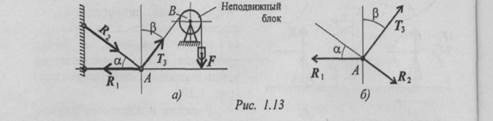
Решение
1. Реакции стержней направлены вдоль стержней, реакции
гибких связей направлены вдоль нитей в сторону натяжения
(рис. 1. 13а).
2. Для определения точного направления усилий в стержнях мысленно убираем последовательно стержни 1 и 2. Анализируем возможные перемещения точки А.
|
|
|
Неподвижный блок с действующими на него силами не рассматриваем.
3. Убираем стержень 1, точка А поднимается и отходит от стены, следовательно, реакция стержня 1 направлена к стене.
4. Убираем стержень 2, точка А поднимается и приближается к стене, следовательно, реакция стержня 2 направлена от стены вниз.
5. Канат тянет вправо.
6. Освобождаемся от связей (рис. 1. 136).
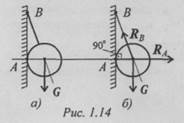
Пример 2. Шар подвешен на нити и опирается на стену (рис. 1. 14а). Определить реакции нити и гладкой опоры (стенки).
Решение
1. Реакция нити — вдоль нити к точке В вверх (рис. 1. 146).
2. Реакция гладкой опоры (стенки) — по нормали от поверхности опоры.
Тема 1. 1. Основные понятия и аксиомы статики 11
Контрольные вопросы и задания
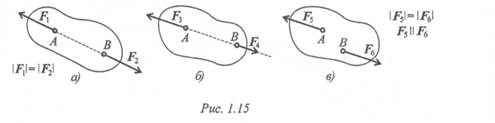
1. Какая из приведенных систем сил (рис. 1. 15) уравновешена?
2. Какие силы системы (рис. 1. 16) можно убрать, не нарушая
механического состояния тела?
3. Тела 1 и 2 (рис. 1. 17) находятся в равновесии. Можно ли
убрать действующие системы сил, если тела абсолютно твердые?
Что изменится, если тела реальные, деформируемые?
4. Укажите возможное направление реакций в опорах (рис. 1. 18).
12 Лекция 2
ЛЕКЦИЯ 2
|
|
|
Тема 1. 2. Плоская система сходящихся сил. Определение равнодействующей геометрическим способом
Знать геометрический способ определения равнодействующей системы сил, условия равновесия плоской системы сходящихся сил.
Уметь определять равнодействующую, решать задачи на равновесие в геометрической форме.
Плоская система сходящихся сил
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся (рис. 2. 1).
Необходимо определить равнодействующую системы сходящихся сил ( F1; F2; F3;. .. ...; Fn ), n — число сил, входящих в систему.
По следствию из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными в одной точке.
|
|
|
