 |
Равнодействующая сходящихся сил
|
|
|
|
Равнодействующая сходящихся сил
Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника сил (4-я аксиома) (рис. 2. 2).

Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последо-
Тема 1. 2. Плоская система сходящихся сил 13
вательно силы, входящие в систему. Образуется многоугольник сил (рис. 2. 3). Вектор равнодействующей силы соединит начало первого вектора с концом последнего.

При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называют геометрическим.
Замечание. При вычерчивании многоугольника обращать внимание на параллельность сторон многоугольника соответствующим векторам сил.
Порядок построения многоугольника сил
1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпадал с началом последующего.
2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
|
|
|
Условие равновесия плоской системы сходящихся сил
При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии,
14 Лекция 2
многоугольник сил этой системы должен быть замкнут.
Если в системе три силы, образуется треугольник сил.
Сравните два треугольника сил (рис. 2. 4) и сделайте вывод о количестве сил, входящих в каждую систему.
Рекомендация. Обратить внимание на направление векторов.

Решение задач на равновесие геометрическим способом
Геометрическим способом удобно пользоваться, если в системе три силы. При решении задач на равновесие тело считать абсолютно твердым (отвердевшим).
Порядок решения задач:
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура. )
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
4. Для уточнения решения рекомендуется определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
Пример 1. Груз подвешен на стержнях и находится в равновесии. Определить усилия в стержнях (рис. 2. 5а).
Решение
1. Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз (5-я аксиома статики) (рис. 2. 5а).
Тема 1. 2. Плоская система сходящихся сил 15
|
|
|
Определяем возможные направления реакций связей «жесткие стержни».

Усилия направлены вдоль стержней.
2. Освободим точку А от связей, заменив действие связей их
реакциями (рис. 2. 56).
3. Система находится в равновесии. Построим треугольник сил.
Построение начнем с известной силы, вычертив вектор F в не котором масштабе.
Из концов вектора F проводим линии, параллельные реакциям R1 и R2.
Пересекаясь, линии создадут треугольник (рис. 2. 5в). Зная масштаб построений и измерив длину сторон треугольника, можно определить величину реакций в стержнях.
4. Для более точных расчетов можно воспользоваться геометри-
ческими соотношениями, в частности теоремой синусов: отношение
стороны треугольника к синусу противоположного угла — величина постоянная
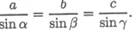
Для данного случая:

16 Лекция 2

Замечание. Если направление вектора (реакции связи) на заданной схеме и в треугольнике сил не совпало, значит, реакция на схеме должна быть направлена в противоположную сторону.
Пример 2. Груз подвешен на стержнях и канатах и находится в равновесии. Определить усилия в стержнях (рис. 2. 6а).
|
|
|


