Решение. Контрольные вопросы и задания. Тема 1.2. Плоская система сходящихся сил. Определение равнодействующей. аналитическим способом

Решение

             

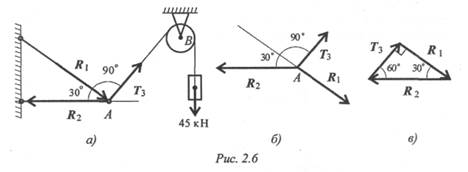
1. Нанесем на схему возможные направления усилий, приложенных в точке А. Реакции стержней — вдоль стержней, усилие от
каната — вдоль каната от точки А к точке В.

2. Груз находится в равновесии, следовательно, в равновесии
находится точка А, в которой пересекаются три силы.

Освободим точку А от связей и рассмотрим ее равновесие (рис. 2. 66).

Замечание. Рассмотрим только силы, приложенные к точке А. Груз растягивает канат силой 45 кН по всей длине, поэтому усилие от каната известно: Тз = 45 кН.

3. Строим треугольник для сил, приложенных в точке А, начиная с известной силы Тз. Стороны треугольника параллельны предполагаемым направлениям сил, приложенных в точке А.

Образовался прямоугольный треугольник (рис. 2. 6в).

                 Тема 1. 2. Плоская система сходящихся сил                                      17

4. Неизвестные реакции стержней можно определить из соотно­шений в прямоугольном треугольнике:

              

 

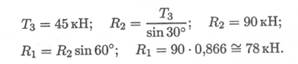
Замечание. При равновесии векторы сил в треуголь­нике направлены один за другим (обходим треугольник по часовой стрелке). Сравним направления сил в треугольнике с принятыми в начале расчета на рис. 1. 26а. Направления совпали, следовательно, направления реакций определены верно.

                 Контрольные вопросы и задания

1. По изображенным многоугольникам сил (рис. 2. 7) решите,
сколько сил входит в каждую систему и какая из них уравновешена.
(Обратить внимание на направление векторов. )

 

         

 

2. Из представленных силовых треугольников выберете тре-­
угольник, построенный для точки А (рис. 2. 8, 2. 9).

            

        

Шар подвешен на нити и находится в равновесии. Обратить внимание на направление реакции от гладкой опоры и условие рав­новесия шара (рис. 2. 8).

18                                                                      Лекция 2                                                                        

 

                             

 

Груз F подвешен на канате и находится в равновесии. Обра­тить внимание на реакции, приложенные к точке А. Силы, не при­ложенные к точке А, не рассматриваются. Не забывать об условии равновесия системы сил (рис. 2. 9).

                                                 Тема 1. 2. Плоская система сходящихся сил                                                   19

ЛЕКЦИЯ 3

Тема 1. 2. Плоская система сходящихся сил.

Определение равнодействующей

аналитическим способом

Знать аналитический способ определения равнодействующей силы, условия равновесия плоской сходящейся системы сил в ана­литической форме.

Уметь определять проекции силы на две взаимно перпендику­лярные оси, решать задачи на равновесие в аналитической форме.

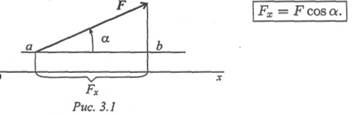
Проекция силы на ось

Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора (рис. 3. 1).

 

                            

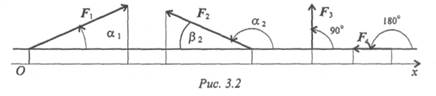
Величина проекции силы на ось равна произведению модуля си­лы на косинус угла между вектором силы и положительным напра­влением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 3. 2).

 

                   

20                                                                                             Лекция 3

                 

                 

Проекция силы на две взаимно перпендикулярные оси (рис. 3. 3).

       

 

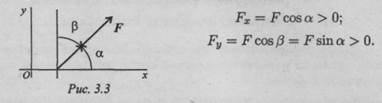
 Определение равнодействующей системы сил аналитическим  

                                              способом

Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равнодействующую геоме­трическим способом. Выберем систему координат, определим про­екции всех заданных векторов на эти оси (рис. 3. 4а). Складываем проекции всех векторов на оси х и у (рис. 3. 46).

                

                 

                 Тема 1. 2. Плоская система сходящихся сил                                 21

Модуль (величину) равнодействующей можно найти по известным проекциям:                    

                                            

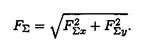
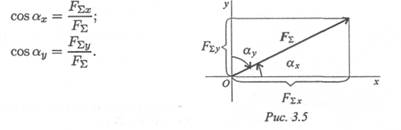
Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующей с осями координат (рис. 3. 5).           

             

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: