 |
Тема 5.1 Механические гармонические колебания.
|
|
|
|
Маятники. Сложение колебаний.
I. Цель практического занятия:
1. Закрепить и углубить знания теоретических вопросов, основных понятий и формул, способов расчёта.
2. Учится применять полученные знания для решения задач по данной теме.
II. Расчёт учебного времени:
| Содержание занятия: | Время (мин.) |
Вступительная часть:
Объявление темы и цели занятия
Контрольный опрос:
|
Контрольный опрос:
1. 
 ν =
ν =  начальная фаза.
начальная фаза.
2. 

3. 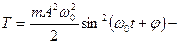 кинетическая;
кинетическая;
 потенциальная;
потенциальная;
 полная энергия.
полная энергия.
4.
а)  ,
,  - жесткость пружины;
- жесткость пружины;
б)  ;
;
I – момент инерции маятника относительно оси колебания;
d – расстояние между точкой подвеса и центром масс.
 - приведенная длина физического маятника.
- приведенная длина физического маятника.
в) 
5. Амплитуда результирующего колебания:  Начальная фаза результирующего колебания:
Начальная фаза результирующего колебания: 
6. 
Основная часть:
Пример №1. Тр. №4.10
Материальная точка совершает гармонические колебания согласно уравнению  , м. определить: 1)амплитуду колебаний; 2)период колебаний; 3)начальную фазу колебаний; 4)максимальную скорость точки; 5)максимальное ускорение точки; 6)через сколько времени после начала отсчёта точка будет проходить через положение равновесия.
, м. определить: 1)амплитуду колебаний; 2)период колебаний; 3)начальную фазу колебаний; 4)максимальную скорость точки; 5)максимальное ускорение точки; 6)через сколько времени после начала отсчёта точка будет проходить через положение равновесия.
|
|
|
Дано:
 ,м ,м
| Решение:
1) А=0,02 м
2)  ; ;  .
3) .
3)  4)
4)  ; ;  м/с
5) м/с
5) 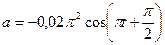
 м/с2
6) м/с2
6)  , тогда: , тогда: 
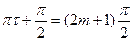 ; ;  
|
А-?
Т-?

|
Пример №2 Тр. №4.11
Материальная точка, совершающая гармонические колебания с частотой 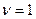 Гц, в момент времени t=0 проходит положение, определяемое координатой
Гц, в момент времени t=0 проходит положение, определяемое координатой  м, со скоростью
м, со скоростью  м/с. Определить амплитуду колебаний.
м/с. Определить амплитуду колебаний.
Дано:
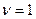 Гц Гц
 м м
 м/с м/с
| Решение:

 Поделим выражения:
Поделим выражения:  ,
Тогда: ,
Тогда:  Из тригонометрического тождества:
Из тригонометрического тождества:
 , тогда , тогда
 Т.к.
Т.к. 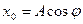 , то , то  м м
|
| А -? |
Пример №3 Тр. №4.16
Полная энергия Е гармонически колеблющейся точки равна
10 мкДж, а максимальная сила Fmax, действующая на точку, равна
-0,5 мН. Написать уравнение движения этой точки, если период Т колебаний равен 4 с,а начальная фаза  =
=  .
.
Дано:
 Дж Дж
 Н Н

| Решение:
Т.к.  ; ; 
 , тогда , тогда  м м
 ,
Тогда: ,
Тогда:  , м , м
|

|
Пример№4 Тр. №4.20
Материальная точка колеблется согласно уравнению  , где А=5см и
, где А=5см и  когда возвращающая сила F в первый раз достигает значения -12мН, потенциальная энергия П точки оказывается равной 0,15 мДж. Определить: 1)момент времени t; 2)соответствующую этому моменту фазу
когда возвращающая сила F в первый раз достигает значения -12мН, потенциальная энергия П точки оказывается равной 0,15 мДж. Определить: 1)момент времени t; 2)соответствующую этому моменту фазу  .
.
Дано:
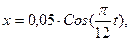 м м
 Н Н
 Дж Дж
| Решение:


 Тогда:
Тогда: 
 и и 
|

|
Пример №5 Тр. №4.25
На горизонтальной пружине жёсткостью k =800 Н/м укреплён шар массой М =4 кг, лежащий на гладком столе, по которому он может скользить без трения. Пуля массой m =10 г, летящая с горизонтальной скоростью 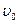 =600 м/с и имеющая в момент удара скорость направленную вдоль оси пружины, попала в шар и застряла в нём. Пренебрегая массой пружины и сопротивлением воздуха, определить: 1)амплитуду колебаний шара; 2)период колебаний шара.
=600 м/с и имеющая в момент удара скорость направленную вдоль оси пружины, попала в шар и застряла в нём. Пренебрегая массой пружины и сопротивлением воздуха, определить: 1)амплитуду колебаний шара; 2)период колебаний шара.
Дано:

| Решение:
 При попадании пули в шар происходит неупругий удар; выполняется закон сохранение импульса:
При попадании пули в шар происходит неупругий удар; выполняется закон сохранение импульса:
 где где  - скорость шара непосредственно после попадания пули.
Шар с пулей начинает колебаться около положения равновесия, т.е. становится пружинным маятником, период которого: - скорость шара непосредственно после попадания пули.
Шар с пулей начинает колебаться около положения равновесия, т.е. становится пружинным маятником, период которого:
 При прохождении положения равновесия шар имеет скорость – И. Эта скорость является максимальной и связана с амплитудой соотношением:
При прохождении положения равновесия шар имеет скорость – И. Эта скорость является максимальной и связана с амплитудой соотношением:
 , следовательно , следовательно 

|
| А-? Т-? |
|
|
|
Пример№6 Тр.№4.28
Однородный диск радиусом R =20см колеблется около горизонтальной оси, проходящей на расстоянии l =15см от центра диска. Определить период Т колебаний диска относительно этой оси.
| Дано: R=0,2м l=0,15м | Решение:
 Диск является физическим маятником, поэтому: Диск является физическим маятником, поэтому:
 . По теореме Штейнера: . По теореме Штейнера:
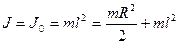 Тогда:
Тогда: 
|
| Т-? |
Пример №7 Тр.№4.32
Маятник состоит из стержня (l =30 см; m =50 г), на верхнем конце которого укреплён маленький шарик (материальная точка массой
m /= 40 г), на нижнем – шарик (R =5 см; М =100 г). Определить период колебания этого маятника около горизонтальной оси, проходящей через точку О в центре стержня.
Дано:

| Решение:
 Найдём центр масс системы,то есть координату y центра масс: Найдём центр масс системы,то есть координату y центра масс:
 Тогда период этого физического маятника:
Тогда период этого физического маятника:

 Тогда: Т=1,24с.
Тогда: Т=1,24с.
|
| Т-? |
Пример№8 Тр. №4.50
Складываются два гармонических колебания одного направления, описываемых уравнениями  см и
см и  см. Определить для результирующего колебания: 1)амплитуду; 2)начальную фазу. Записать уравнение результирующего колебания и представить векторную диаграмму сложения амплитуд.
см. Определить для результирующего колебания: 1)амплитуду; 2)начальную фазу. Записать уравнение результирующего колебания и представить векторную диаграмму сложения амплитуд.
Дано:

| Решение:
Найдём амплитуду и начальную фазу
результирующего колебания:
 Уравнение результирующего колебания:
Уравнение результирующего колебания:


|
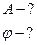
|
Пример№9 Тр.№4.58
Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями  и
и  , где А, В и
, где А, В и 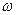 - положительные постоянные. Определить уравнение траектории точки, вычертить её с нанесением масштаба, указав направление её движения по этой траектории.
- положительные постоянные. Определить уравнение траектории точки, вычертить её с нанесением масштаба, указав направление её движения по этой траектории.
Дано:

| Решение:


 - уравнение эллипса. - уравнение эллипса.

|
| y(x)-? |
Пример№10 Тр.№4.60
Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями  и
и  . Определить уравнение траектории точки и вычертить её с нанесением масштаба.
. Определить уравнение траектории точки и вычертить её с нанесением масштаба.
|
|
|
Дано:

| Решение:

 - уравнение траектории. - уравнение траектории.

|
| y(x)-? |
Заключительная часть:
Задание на самостоятельное решение:
Т.И.Трофимова «Сборник задач по курсу физики»:
№4.3; 4.7; 4.13; 4.15; 4.23; 4.29; 4.31; 4.36; 4.49; 4.59.
|
|
|


