 |
Тема 2.1 Динамика материальной точки и тела, движущегося поступательно.
|
|
|
|
I. Цель практического занятия:
1. Закрепить и углубить знание теоретических вопросов, основных понятий и формул, законов динамики материальной точки и поступательного движения твёрдого тела.
2. Учится применять полученные знания для решения задач по данной теме.
II. Расчёт учебного времени:
| Содержание занятия | Время (мин) |
Вступительная часть:
Объявление темы и цели занятия
Контрольный опрос:
|
Контрольный опрос:
1. I закон: если  , то
, то 
II закон: 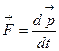 или
или  ;
;
III закон: 
2. Импульс тела: 

3. Закон сохранения импульса для замкнутой системы: 
4. Сила трения скольжения: 
5. Сила тяжести: 
6. Если материальная точка движется по кривой, то сила, действующая на неё, может быть разложена на две составляющие- тангенс и нормальную.  ;
; 
Основная часть.
Пример№1. Тр.№1.43
Тело массой m =2 кг движется прямолинейно по закону S=A-Bt+Ct2-Dt3 (C =2 м/с2, D =0,4 м/с3). Определить силу, действующую на тело в конце первой секунды движения.
| Дано: m =2кг S=A-Bt+Ct2-Dt3 C =2м/с2 D =0,4м/с3 t =1c | Решение:
По II закону Ньютона  Найдём ускорение тела:
Найдём ускорение тела:
 тогда:
тогда: 
|
| F -? |
Пример№2. Тр.№1.52
Тело массой m движется в плоскости x y по закону x=A cos 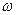 t, y=B sin
t, y=B sin 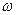 t, где А В и
t, где А В и 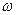 -некоторые постоянные. Определить модуль силы, действующей на это тело.
-некоторые постоянные. Определить модуль силы, действующей на это тело.
Дано:
x=A cos 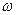 t
y=B sin t
y=B sin 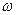 t t
| Решение:
Найдём проекции скорости и ускорения на оси x и y:
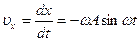 ; ;  ; ;
 ; ;  .
Найдём полное ускорение тела: .
Найдём полное ускорение тела:
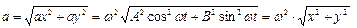 тогда модуль силы будет равен:
тогда модуль силы будет равен:

|
| F-? |
|
|
|
Пример№3. Чер.№2-3
К пружинным весам подвешен блок. Через блок перекинут шнур, к концам которого привязали грузы массами m1 =1,5 кг и m2 =3 кг. Каково будет показание весов во время движения грузов? Массой блока и шнура пренебречь.
| Дано: m1 =1,5кг m2 =3кг | Решение:
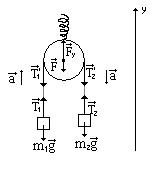 Составим уравнение динамики движения гру движения грузов: Составим уравнение динамики движения гру движения грузов:
 В проекциях на ось y:
В проекциях на ось y:
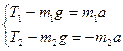 Так как шнур невесомый и нерастяжимый, а блок невесомый,то
Так как шнур невесомый и нерастяжимый, а блок невесомый,то 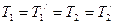 , тогда: , тогда:
 ; ;  .
Решая уравнение, получим: .
Решая уравнение, получим: 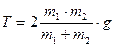 . А сила, с которой блок действует на весы, равна: . А сила, с которой блок действует на весы, равна:
 если известен радиус блока R, то его угловое ускорение:
если известен радиус блока R, то его угловое ускорение:

|
| F -? |
Пример№4. Тр.№1.51
В установке углы 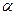 и
и  с горизонтом соответственно равны 30 и 45°, массы тел m1 =0,45 кг и m2 =0,5 кг. Считая нить и блок невесомыми и пренебрегая силами трения, определить: 1) ускорение, с которым движутся тела; 2) силу натяжения нити.
с горизонтом соответственно равны 30 и 45°, массы тел m1 =0,45 кг и m2 =0,5 кг. Считая нить и блок невесомыми и пренебрегая силами трения, определить: 1) ускорение, с которым движутся тела; 2) силу натяжения нити.
Дано:
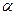 =30° =30°
 =45°
m1 =0,45 кг
m2 =0,5 кг =45°
m1 =0,45 кг
m2 =0,5 кг
| Решение:
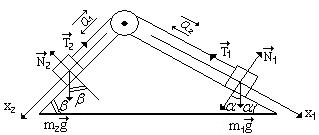 Составим уравнение движения для тел:
Составим уравнение движения для тел:
 В проекциях на выбранные оси (x и x2):
В проекциях на выбранные оси (x и x2):
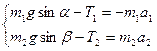 Так как нить и блок невесомы, а трение отсутствует: Т1=Т2; а1=а2 и:
Так как нить и блок невесомы, а трение отсутствует: Т1=Т2; а1=а2 и:
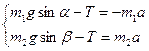 Вычитая, получим:
Вычитая, получим: 


|
| а -? Т -? |
Пример№5. Тр.№1.57
По наклонной плоскости с углом 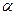 наклона к горизонту, равным 30°, скользит тело. Определить скорость тела в конце второй секунды от начала скольжения, если коэффициент трения
наклона к горизонту, равным 30°, скользит тело. Определить скорость тела в конце второй секунды от начала скольжения, если коэффициент трения  = 0,15.
= 0,15.
Дано:
 30° 30°
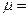 0,15
t= 2с 0,15
t= 2с
| Решение:
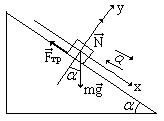 Так как тело соскальзывает без начальной скорости, то:
Так как тело соскальзывает без начальной скорости, то:  Запишем уравнение движения для тела:
Запишем уравнение движения для тела:  В проекциях на выбранной оси:
В проекциях на выбранной оси:
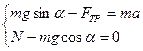 Так как
Так как  ,то ,то  Тогда:
Тогда: 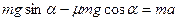 и
и 
|
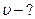
|
Пример№6. Чер.2.11
Тело массой m =5 кг брошено под углом 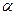 =30° к горизонту с начальной скоростью
=30° к горизонту с начальной скоростью 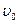 =20 м/с. Пренебрегая сопротивлением воздуха найти: 1) импульс силы F, действующей на тело, за время его полёта;
=20 м/с. Пренебрегая сопротивлением воздуха найти: 1) импульс силы F, действующей на тело, за время его полёта;
2) изменение  импульса тела за время полёта.
импульса тела за время полёта.
Дано:
m =5 кг
 30° 30°
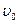 =20м/с =20м/с
| Решение:
 На тело действует сила тяжести, импульс которой:
На тело действует сила тяжести, импульс которой:
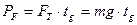 Из примера №3 (зан. №2)
Из примера №3 (зан. №2)  Таким образом
Таким образом  Так как
Так как  , то , то 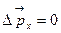 Поэтому:
Поэтому:
 Следовательно, подтверждается, что:
Следовательно, подтверждается, что:
 - в случае, если F=const. - в случае, если F=const.
|

|
|
|
|
Пример№7. Тр.№1.64
Снаряд массой m=5кг, вылетевший из орудия, в верхней точке траектории имеет скорость  =300м/с. В этой точке он разорвался на два осколка, причём больший осколок массой m1 =3кг полетел в обратном направлении со скоростью
=300м/с. В этой точке он разорвался на два осколка, причём больший осколок массой m1 =3кг полетел в обратном направлении со скоростью 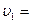 100м/с. Определить скорость
100м/с. Определить скорость  второго, меньшего, осколка.
второго, меньшего, осколка.
Дано:
m =5кг
 =300м/с
m1 =3кг =300м/с
m1 =3кг
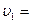 100м/с 100м/с
| Решение:
 Так как при разрыве на осколки действуют силы, гораздо больше, чем сила тяжести и др., то систему можно считать замкнутой и применять для неё закон сохранения импульса: Так как при разрыве на осколки действуют силы, гораздо больше, чем сила тяжести и др., то систему можно считать замкнутой и применять для неё закон сохранения импульса:  В проекциях на оси:
В проекциях на оси:  Из второго уравнения
Из второго уравнения 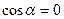 ; т.е. ; т.е.  Следовательно, второй осколок движется в том же направлении, что и снаряд до разрыва. Поэтому:
Следовательно, второй осколок движется в том же направлении, что и снаряд до разрыва. Поэтому:
 и и

|
 -? -?
|
Пример№8. Чер.№ 2.29; 2.30
На полу стоит тележка в виде длинной доски, снабженной легкими колёсами. На одном конце доски стоит человек. Масса человека M =60 кг, масса доски m =20 кг. С какой скоростью U (относительно пола) будет двигаться тележка, если человек пойдёт вдоль доски со скоростью (относительно доски)  =1 м/с? Массой колёс пренебречь. Трение во втулках не учитывать.
=1 м/с? Массой колёс пренебречь. Трение во втулках не учитывать.
В предыдущей задаче найти, на какое расстояние d:
1) передвинется тележка, если человек перейдёт на другой конец доски; 2) переместится человек относительно пола;
3)переместится центр масс системы тележка-человек относительно доски и относительно пола. Длина l доски равна 2 м.
Дано:
M =60 кг
m =20 кг
 =1 м/с
l =2 м =1 м/с
l =2 м
| Решение:
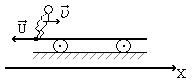 1. Так как трением пренебрегаем, то систему можно считать замкнутой и использовать для неё закон сохранения импульса:
1. Так как трением пренебрегаем, то систему можно считать замкнутой и использовать для неё закон сохранения импульса:
 , где , где  -скорость человека относительно пола. В проекциях на выбранную ось: -скорость человека относительно пола. В проекциях на выбранную ось:
 2. Найдём перемещение тележки.
Запишем закон сохранения импульса в виде:
2. Найдём перемещение тележки.
Запишем закон сохранения импульса в виде:  Обозначим время движения человека по доске-
Обозначим время движения человека по доске- 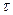 . Тележка будет двигаться в течение этого же времени. Тогда: . Тележка будет двигаться в течение этого же времени. Тогда:
 так как
так как 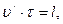 а а  -перемещение тележки, то: -перемещение тележки, то:
 и и  3. Так как скорость человека относительно пола
3. Так как скорость человека относительно пола 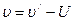 , то перемещение человека относительно пола: , то перемещение человека относительно пола: 
|
| U -? d -? S -? |
Пример№9. Чер.№2.40
Грузик, привязанный к нити длиной l =1 м, описывает окружность в горизонтальной плоскости. Определить период T обращения, если нить отклонена на угол  60° от вертикали.
60° от вертикали.
|
|
|
Дано:
l =1 м
 60° 60°
|  Решение:
Равнодействующая сил Решение:
Равнодействующая сил  и и 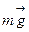 направлена к центру окружности, по которой вращается грузик. Вращение грузика равномерное и равнодействующая сил направлена к центру и равна: направлена к центру окружности, по которой вращается грузик. Вращение грузика равномерное и равнодействующая сил направлена к центру и равна:
 из рисунка:
из рисунка:  ,
то есть ,
то есть  где где 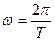 Тогда:
Тогда: 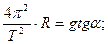 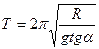 Так как
Так как  то то 
|
| T -? |
Пример№10. Чер.№2.46
Какую наибольшую скорость  может развить велосипедист, проезжая закругление радиусом R =50 м, если коэффициент трения скольжения
может развить велосипедист, проезжая закругление радиусом R =50 м, если коэффициент трения скольжения  между шинами и асфальтом равен 0,3? Каков угол
между шинами и асфальтом равен 0,3? Каков угол  отклонения велосипеда от вертикали, когда велосипедист движется по закруглению?
отклонения велосипеда от вертикали, когда велосипедист движется по закруглению?
Дано:
R =50 м
 0,3 0,3
| Решение:
 Так как центр масс не перемещается по вертикали, то:
Так как центр масс не перемещается по вертикали, то:  Центростремительное ускорение сообщает
сила трения:
Центростремительное ускорение сообщает
сила трения:  .
Направление результирующей силы .
Направление результирующей силы 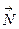 и и 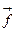 должно совпадать с направлением вдоль велосипеда к центру масс системы.
Тогда: должно совпадать с направлением вдоль велосипеда к центру масс системы.
Тогда: 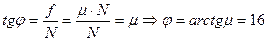 °42/
Так как °42/
Так как  то
то 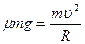 и и 
|
 -? -?
 ? ?
|
Заключительная часть:
Задание на самостоятельное решение:
- «Задачник по физике» под ред. А.Г. Чертова № 2-7; 2-12; 2-27.
- Т.И.Трофимова «Сборник задач по курсу физики» №1.50; 1.67; 1.68.
|
|
|


