 |
Тема 4.1 Элементы механики жидкостей
|
|
|
|
I. Цель практического занятия:
- Закрепить и углубить знание теоретических вопросов, основных понятий и формул, уравнений механики жидкостей.
- Учиться применять полученные знания для решения задач по данной теме.
II. Расчёт учебного времени:
| Содержание занятия | Время (мин.) |
Вступительная часть:
Объявление темы и цели занятия.
Контрольный опрос:
|
Контрольный опрос
- Уравнение неразрывности:
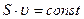
- Уравнение Бернулли:

 - статическое давление жидкости для данного сечения трубки тока;
- статическое давление жидкости для данного сечения трубки тока;
 - динамическое давление для этого же сечения;
- динамическое давление для этого же сечения;
 - гидростатическое давление.
- гидростатическое давление.
- Для горизонтальной трубки тока:

- Формула Стокса, определяющая силу сопротивления, действующую на медленно движущийся в вязкой среде шарик:
 ,
,
 - радиус шарика;
- радиус шарика;
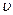 - его скорость.
- его скорость.
- Формула Пуазейля, определяющая объем жидкости, протекающий за время t через капиллярную трубку диной l:

R – радиус трубки;
 - разность давлений на концах трубки.
- разность давлений на концах трубки.
Основная часть
Пример №1 Чер.№7-4
Горизонтальный цилиндр насоса имеет диаметр 20 см. в нём движется со скоростью  м/с поршень, выталкивая воду через отверстие диаметром d2 =2см. С какой скоростью
м/с поршень, выталкивая воду через отверстие диаметром d2 =2см. С какой скоростью  будет вытекать вода из отверстия? Каково будет избыточное давление p воды в цилиндре?
будет вытекать вода из отверстия? Каково будет избыточное давление p воды в цилиндре?
|
|
|
Дано:

| Решение:
Из уравнения неразрывности:

 Тогда:
Тогда:  Т.к. труба горизонтальная, то:
Т.к. труба горизонтальная, то: 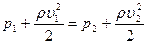 Поэтому:
Поэтому: 
|

|
Пример №2 Тр.№1.220
Площадь поршня, вставленного в горизонтально расположенный, налитый водой цилиндр, S1 =1,5 см2, а площадь отверстия S2 =0,8 мм2. Пренебрегая трением и вязкостью, определить время t, за которое вытечет вода из цилиндра, если на поршень действовать постоянной силой F =5Н, а ход поршня l =5 см. плотность воды  =1000 кг/м3.
=1000 кг/м3.
Дано:

| Решение: 
 Объем вытекающей из цилиндра воды можно расписать:
Объем вытекающей из цилиндра воды можно расписать: 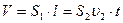 Тогда время вытекания воды:
Тогда время вытекания воды: 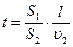 Цилиндр расположен горизонтально,
поэтому:
Цилиндр расположен горизонтально,
поэтому:  т.е. т.е.  Из уравнения неразрывности:
Из уравнения неразрывности:  , тогда , тогда  и и
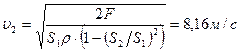 . И, окончательно . И, окончательно 
|
| t -? |
Пример №3 Тр.№1.214
В бочку заливается вода со скоростью 200 см3/с. На дне бочки образовалось отверстие площадью поперечного сечения 0,8 см2. Пренебрегая вязкостью воды, определить уровень воды в бочке.
Дано:

| Решение:
 Т.к. уровень воды в бочке постоянный, то объем залитой за
Т.к. уровень воды в бочке постоянный, то объем залитой за  воды равен объему вылившейся воды: воды равен объему вылившейся воды:
 то есть, то есть,  За нулевой уровень выберем дно бочки, тогда:
За нулевой уровень выберем дно бочки, тогда:
 ; ; 
|
| h -? |
Пример № 4 Тр.№1.226
По горизонтальной трубе переменного сечения течёт вода. Площади поперечного сечения трубы на разных её участках соответственно равны S1 =10 см2 и S2 =20 см2. Разность уровней  воды в вертикальных трубках одинакового сечения составляет 20 см. Определить объём воды, проходящей за 1с через сечение трубы.
воды в вертикальных трубках одинакового сечения составляет 20 см. Определить объём воды, проходящей за 1с через сечение трубы.
Дано:
S1 =10-3м2
S2 =2·10-3м2
 =0,2м
t =1с =0,2м
t =1с
| Решение:
Из уравнения неразрывности струи:
Из уравнения Бернулли:
Тогда: Объём воды, проходящий за 1с через сечение трубы:
| |||
| V/-? |
Пример№5
Цилиндрический бак высотой h=1 м наполнен до краёв водой. За какое время вся вода выльется из отверстия, расположенного у дна бака? Площадь поперечного сечения отверстия в 400 раз меньше площади бака.
|
|
|
Дано:
h =1м

|  Решение: Решение:
 - скорость опускания уровня воды в баке. - скорость опускания уровня воды в баке.
 - скорость вытекания воды из бака.
Из уравнения неразрывности: - скорость вытекания воды из бака.
Из уравнения неразрывности:  Из уравнения Бернулли:
Из уравнения Бернулли:  ,
где y – уровень воды в баке.
Тогда: ,
где y – уровень воды в баке.
Тогда:  и
и  Считаем, что за малый промежуток времени dt скорость
Считаем, что за малый промежуток времени dt скорость
 мало изменится, а уровень воды понизится на: мало изменится, а уровень воды понизится на:
 Откуда:
Откуда:  Тогда:
Тогда:

|
| t-? |
Пример №6. Тр.№1.232
В боковой поверхности цилиндрического сосуда, стоящего на горизонтальной поверхности, имеется отверстие, поперечное сечение которого значительно меньше поперечного сечения самого сосуда. Отверстие расположено на расстоянии h1 =49см от уровня воды в сосуде, который поддерживается постоянным, и на расстоянии h2 =25см от дна сосуда. Пренебрегая вязкостью воды, определить расстояние по горизонтали от отверстия до места, куда попадает струя воды.
| Дано: h1 =0,49м h2 =0,25м | Решение:
Из уравнения Бернулли: 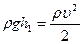 ; ;
  Найдём t/:
Найдём t/:  ; ;  и и 
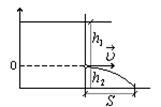 Тогда: Тогда: 
|
| S -? |
Пример №7 Тр.№1.239
Стальной шарик (плотность  =9г/см3) диаметром d =0,8см падает с постоянной скоростью в касторовом масле (
=9г/см3) диаметром d =0,8см падает с постоянной скоростью в касторовом масле ( =0,96г/см3, динамическая вязкость
=0,96г/см3, динамическая вязкость  =0,99Па·с.) Учитывая, что критическое значение числа Рейнольдса Reкр=0,5, определить характер движения масла, обусловленный падением в нём шарика.
=0,99Па·с.) Учитывая, что критическое значение числа Рейнольдса Reкр=0,5, определить характер движения масла, обусловленный падением в нём шарика.
Дано:
 =9·103кг/м3
d =8·10-3м =9·103кг/м3
d =8·10-3м
 =0,96·103кг/м3 =0,96·103кг/м3
 =0,99Па·с
Reкр=0,5 =0,99Па·с
Reкр=0,5
| Решение:
При установившемся движении шарика
( ): ): 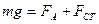 ,
FA – сила Архимеда;
FСТ – сила внутреннего трения. ,
FA – сила Архимеда;
FСТ – сила внутреннего трения.
 Так как
Так как
 , то , то  .
Для шара небольшого радиуса, движущегося в вязкой
жидкости, число Рейнольдса: .
Для шара небольшого радиуса, движущегося в вязкой
жидкости, число Рейнольдса:  , где
d –диаметр шарика.
Тогда: , где
d –диаметр шарика.
Тогда: 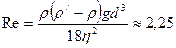 Так как
Так как  то движение масла,
обусловленное падением в него шарика, имеет
турбулентный характер. то движение масла,
обусловленное падением в него шарика, имеет
турбулентный характер.
|
| Re-? |
Пример№8 Тр.№1.241
В боковую поверхность сосуда вставлен горизонтальный капилляр внутренним диаметром d =2мм и длиной l =1,2см. Через капилляр вытекает касторовое масло (плотность  =0,96г/см3, динамическая вязкость
=0,96г/см3, динамическая вязкость  =0,99Па·с), уровень которого в сосуде поддерживается постоянным на высоте h =30см выше капилляра. Определить время, которое требуется для протекания через капилляр 10см3 масла.
=0,99Па·с), уровень которого в сосуде поддерживается постоянным на высоте h =30см выше капилляра. Определить время, которое требуется для протекания через капилляр 10см3 масла.
Дано:
 =0,96·103кг/м3 =0,96·103кг/м3
 =0,99Па·с
l =0.012м
r =10-3м
h =0,3м
V =10-5м3 =0,99Па·с
l =0.012м
r =10-3м
h =0,3м
V =10-5м3
| Решение:
Из формулы Пуазейля:
 , где , где  .
Тогда: .
Тогда: 
|
| t-? |
Заключительная часть
- Задаётся задание на самостоятельное решение:
Т.И.Трофимова «Сборник задач по курсу физики.»
|
|
|
№1.216; 1.218; 1.233; 1.238.
|
|
|






 .
.
