 |
Тема 5.2 Затухающие и вынужденные колебания.
|
|
|
|
I. Цель практического занятия:
3. Закрепить и углубить знания теоретических вопросов, основных понятий и формул, способов расчёта характеристик колебаний.
4. Учится применять полученные знания для решения задач по данной теме.
II. Расчёт учебного времени:
| Содержание занятия: | Время (мин.) |
Вступительная часть:
Объявление темы и цели занятия
Контрольный опрос:
|
Контрольный опрос:
1.  ;
;
S-колеблющаяся величина;
 -коэффициент затухания;
-коэффициент затухания;
 -коэффициент сопротивления;
-коэффициент сопротивления;
 -собственная частота колебаний без учёта сопротивления.
-собственная частота колебаний без учёта сопротивления.
Решение этого уравнения:  ,
,
 -частота затухающих колебаний.
-частота затухающих колебаний.
 -амплитуда затухающих колебаний.
-амплитуда затухающих колебаний.
2.  ;
; 
3. 
4. 
5. 
6. 
 ,
,
где  ;
; 
7.  ;
; 
Основная часть:
Пример №1 Тр.№4.67
Начальная амплитуда затухающих колебаний маятника А0 =3 см. по истечении t1 =10 с А1 =1 см. Определить, через сколько времени амплитуда колебаний станет равной А2 =0,3 см.
Дано:

| Решение:
Так как амплитуда затухающих колебаний 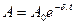 ,то ,то
 Тогда:
Тогда:  и и  ; ;  Прологарифмируем выражение:
Прологарифмируем выражение:  ,
тогда ,
тогда  . Таким образом . Таким образом 
|

|
|
|
|
Пример№2 Тр. №4.68
Тело массой m =0,6 кг, подвешенное к спиральной пружине жёсткостью k =30 н/м, совершает в некоторой среде упругие колебания. Логарифмический декремент колебаний Q =0,01. Определить: 1)время t, за которое амплитуда колебаний уменьшится в 3 раза; 2)число N полных колебаний, которые должна совершить гиря, чтобы произошло подобное уменьшение амплитуды.
Дано:

| Решение:
Так как  , тогда , тогда 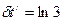 и и  Так как
Так как  и и  ,то ,то  Тогда:
Тогда:  Найдём число колебаний, за которое произошло данное уменьшение амплитуды:
Найдём число колебаний, за которое произошло данное уменьшение амплитуды: 
  то есть
то есть  , а так как , а так как  , то , то  ,
что мы и использовали. ,
что мы и использовали. 
|

|
Пример№3 Тр. №4.70
При наблюдении затухающих колебаний выяснилось, что для двух последовательных колебаний амплитуда второго меньше амплитуды первого на 60%. Период затухающих колебаний Т =0,5 с. Определить: 1)коэффициент затухания  ; 2)для тех же условий частоту
; 2)для тех же условий частоту  незатухающих колебаний.
незатухающих колебаний.
Дано:

| Решение:
0,6= 

   Так как
Так как  , то , то  Тогда:
Тогда: 
|

|
Пример №4 Тр.№4.74
Частота свободных колебаний некоторой системы  =65 рад/с, а её добротность Q =2. Определить собственную частоту
=65 рад/с, а её добротность Q =2. Определить собственную частоту  колебаний этой системы.
колебаний этой системы.
Дано:

| Решение:
Так как 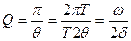 , тогда: , тогда:  Так как
Так как  , то , то 
|

|
Пример №5 Тр.№4.85
Собственная частота  колебаний некоторой системы составляет 500 Гц. Определить частоту
колебаний некоторой системы составляет 500 Гц. Определить частоту  затухающих колебаний этой системы, если резонансная частота
затухающих колебаний этой системы, если резонансная частота 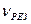 =499 Гц.
=499 Гц.
Дано:

| Решение:
Частота затухающих колебаний  Резонансная частота:
Резонансная частота: 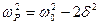 Так как
Так как  , то , то  Тогда:
Тогда:  Так как
Так как  , то , то 
|

|
Пример №6 Тр.№4.86
Период затухающих колебаний системы составляет 0,2 с, а отношение амплитуд первого и шестого колебаний равно 13. Определить резонансную частоту данной колебательной системы.
Дано:

| Решение:
Так как  , то , то  и и 
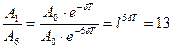
 ; ; 

|

|
Пример №7 Тр.№4.88
Гиря массой m =400 г, подвешенная на спиральной пружине жёсткостью k =40 н/м, опущена в масло. Коэффициент сопротивления r для этой системы составляет 0,5 кг/с. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону  , Н. Определить: 1)амплитуду вынужденных колебаний, если частота вынуждающей силы вдвое меньше собственной частоты колебаний; 2)частоту вынуждающей силы, при которой амплитуда вынужденных колебаний максимальна; 3)резонансную амплитуду.
, Н. Определить: 1)амплитуду вынужденных колебаний, если частота вынуждающей силы вдвое меньше собственной частоты колебаний; 2)частоту вынуждающей силы, при которой амплитуда вынужденных колебаний максимальна; 3)резонансную амплитуду.
|
|
|
Дано:
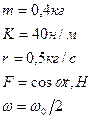
| Решение:
Амплитуда вынужденных колебаний:  ,
где ,
где  ; ;  ; ; 
 А =0,0332м.
А =0,0332м.

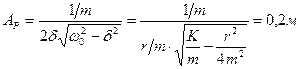
|

|
Пример №8 Тр.№4.89
Гиря массой m =20 г, подвешенная на спиральной пружине жёсткостью k =50 н/м, совершает колебания в вязкой среде с коэффициентом сопротивления r =0,2 кг/с. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону  , Н. Определить: 1)частоту
, Н. Определить: 1)частоту  собственных колебаний; 2)резонансную частоту
собственных колебаний; 2)резонансную частоту 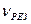 ; 3)резонансную амплитуду АРЕЗ; 4)статическое отклонение.
; 3)резонансную амплитуду АРЕЗ; 4)статическое отклонение.
Дано:

| Решение:




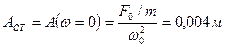
|

|
Заключительная часть:
Задание на самостоятельное решение:
Т.И.Трофимова. «Сборник задач по курсу физики»:
№ 4.64; 4.66; 4.71; 4.73; 4.84; 4.87.
Тема 5.3 Упругие волны.
I. Цель практического занятия:
- Закрепить и углубить знание теоретических вопросов, основных понятий и формул, способов расчёта характеристик бегущих и стоячих механических волн, исследовать явление интерференции механических волн и эффект Доплера в акустике.
- Учиться применять полученные знания для решения задач по данной теме.
II. Расчёт учебного времени:
| Содержание занятия | Время (мин.) |
Вступительная часть:
Объявление темы и цели занятия.
Контрольный опрос:
|
Контрольный опрос:
-
 ;
;  ;
;
 - длина волны;
- длина волны; 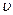 - скорость;
- скорость;  -частота; Т -период.
-частота; Т -период.
|
|
|
 смещение точки с координатой x в момент времени t от положения равновесия.
смещение точки с координатой x в момент времени t от положения равновесия.
 - волновое число.
- волновое число.
-
 фазовая скорость.
фазовая скорость.
 - групповая скорость.
- групповая скорость.
 - амплитуда стоячей волны.
- амплитуда стоячей волны.
-
 1; 2;…-координаты узлов.
1; 2;…-координаты узлов.
 m= 0; 1; 2;-координаты пучности.
m= 0; 1; 2;-координаты пучности.
-
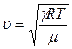 ;
;  - постоянная Пуассона.
- постоянная Пуассона. -
 ,
,  -сближение источника с приёмником;
-сближение источника с приёмником;  - удаление источника и приёмника друг от друга.
- удаление источника и приёмника друг от друга.
Основная часть
Пример№1 Тр.№4.117
Две точки лежат на луче и находятся от источника колебаний на расстояниях x1 =4 м и x2 =7 м. период колебаний Т =20 мс и скорость 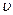 распространения волны равна 300 м/с. Определить разность фаз колебаний этих точек.
распространения волны равна 300 м/с. Определить разность фаз колебаний этих точек.
Дано:

| Решение:
Для точек с координатами x1 и x2 колебания
будут происходить в соответствии с выражениями:
 Поэтому фазы колебаний будут равны:
Поэтому фазы колебаний будут равны:
 ; ; 

|

|
Пример№2 Тр.№4.118
Волна распространяется в упругой среде со скоростью
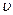 =150 м/с. Определить частоту
=150 м/с. Определить частоту  колебаний, если минимальное расстояние
колебаний, если минимальное расстояние 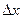 между точками среды, фазы колебаний которых противоположны, равно 0,75 м.
между точками среды, фазы колебаний которых противоположны, равно 0,75 м.
Дано:

| Решение:
Используем формулу, полученную в предыдущем
задании:


|

|
Пример№3 Тр.№4.120
Звуковые колебания с частотой  =450 Гц и амплитудой
=450 Гц и амплитудой
А =0,3 мм распространяются в упругой среде. Длина волны  =80 см. определить: 1)скорость распространения волн; 2)максимальную скорость частиц среды.
=80 см. определить: 1)скорость распространения волн; 2)максимальную скорость частиц среды.
Дано:

| Решение:
Скорость распространения волн:
 Из уравнения бегущей волны:
Из уравнения бегущей волны:
 Можно определить зависимость скорости колебания частицы с координатой x от времени:
Можно определить зависимость скорости колебания частицы с координатой x от времени:

|

|
Пример№4 Тр.№4.121
Плоская синусоидальная волна распространяется вдоль прямой, совпадающей с положительным направлением оси x в среде, не поглощающей энергию, со скоростью 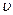 =10 м/с. Две точки, находящиеся на этой прямой на расстояниях x1 =7м и x2 =10м от источника колебаний, колеблются с разностью фаз
=10 м/с. Две точки, находящиеся на этой прямой на расстояниях x1 =7м и x2 =10м от источника колебаний, колеблются с разностью фаз  . Амплитуда волны А =5 см. Определить: 1)длину волны
. Амплитуда волны А =5 см. Определить: 1)длину волны  ; 2)уравнение волны; 3)смещение второй точки в момент времени
; 2)уравнение волны; 3)смещение второй точки в момент времени 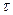 =2 с.
=2 с.
Дано:

| Решение:
Используем выражение для разности фаз колебаний точек среды, полученное в примере №1:
 ; ;  ; ; 
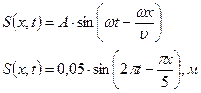 Смещение второй точки в момент времени
Смещение второй точки в момент времени  : :

|

|
|
|
|
Пример№5 Тр.№4.128
Два когерентных источника посылают поперечные волны в одинаковых фазах. Периоды колебаний Т =0,2 с. Скорость распространения волн в среде 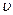 =800 м/с. Определить, при какой разности хода в случае наложения волн будет наблюдаться:
=800 м/с. Определить, при какой разности хода в случае наложения волн будет наблюдаться:
1) ослабление колебаний; 2) усиление колебаний.
Дано:

| Решение:
Уравнения бегущих волн от каждого из источников:
 В результате наложения волн, распространяющихся в одном направлении от когерентных источников, получится волна, бегущая в том же направлении, с той же частотой:
В результате наложения волн, распространяющихся в одном направлении от когерентных источников, получится волна, бегущая в том же направлении, с той же частотой:
 Амплитуда результирующей волны может быть найдена с помощью метода векторных диаграмм (см. лекции):
Амплитуда результирующей волны может быть найдена с помощью метода векторных диаграмм (см. лекции):
 Результирующая амплитуда будет минимальной, т.е. будет наблюдаться ослабление колебаний, если:
Результирующая амплитуда будет минимальной, т.е. будет наблюдаться ослабление колебаний, если:
   0; 1; 2;… 0; 1; 2;…
  Колебания будут усиливаться, если:
Колебания будут усиливаться, если:
   0; 1; 2;… 0; 1; 2;…

|
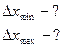
|
Пример№6 Тр.№4.130
Два динамика расположены на расстоянии d =2,5 м друг от друга и воспроизводят один и тот же музыкальный тон на частоте  =1500 Гц. Приёмник находится на расстоянии l =4 м от центра динамиков. Принимая скорость звука
=1500 Гц. Приёмник находится на расстоянии l =4 м от центра динамиков. Принимая скорость звука 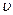 =340 м/с, определить на какое расстояние от центральной линии параллельно динамикам надо отодвинуть приёмник, чтобы он зафиксировал первый интерференционный минимум.
=340 м/с, определить на какое расстояние от центральной линии параллельно динамикам надо отодвинуть приёмник, чтобы он зафиксировал первый интерференционный минимум.
Дано:

| Решение:
 Как было показано в примере №5, максимум интерференции двух когерентных волн наблюдается если: Как было показано в примере №5, максимум интерференции двух когерентных волн наблюдается если:
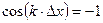 и и  Первый минимум будет наблюдаться при n=0:
Первый минимум будет наблюдаться при n=0:
 ; то есть ; то есть 
 .
Из геометрических соображений: .
Из геометрических соображений:  ; ; 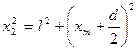 ; ;  Считая, что
Считая, что  то: то:  Так как
Так как  , то , то   Тогда:
Тогда:  
|

|
Пример№7 Тр.№4.134
Определить длину волны  , если расстояние
, если расстояние  между первым и четвёртым узлами стоячей волны равно 30см.
между первым и четвёртым узлами стоячей волны равно 30см.
Дано:

| Решение:
Координаты узлов стоячей волны:  ,
а расстояние между первым и четвёртым узлами: ,
а расстояние между первым и четвёртым узлами:
 Тогда:
Тогда: 
|

|
Пример№8 Тр №4.147
Скорость распространения звуковой волны в газе с молярной массой
М =2,9·10-2 кг/моль при t =20°С составляет 343 м/с. Определить отношение молярных теплоёмкостей газа при постоянных давлении и объёме.
Дано:

| Решение:
Используем формулу скорости звука в газе:
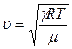 
|

|
Пример№9 Тр. №4.154
Электропоезд проходит со скоростью 54 км/ч мимо неподвижного приёмника и даёт гудок, частота которого 300 Гц. Принимая скорость звука равной 340 м/с, определить частоту тона звукового сигнала гудка поезда.
Дано:

| Решение:
Частота, воспринимаемая приёмником
при приближении электропоезда:  при удалении:
при удалении: 

|

|
Пример№10 Тр.№4.155
Поезд проходит со скоростью 54 км/ч мимо неподвижного приёмника и подаёт звуковой сигнал. Приёмник воспринимает скачок частотой  =53 Гц. Принимая скорость звука равной 340 м/с, определить частоту тона звукового сигнала гудка поезда.
=53 Гц. Принимая скорость звука равной 340 м/с, определить частоту тона звукового сигнала гудка поезда.
|
|
|
Дано:

| Решение:
Используя результат, полученный в предыдущей задаче:


|

|
Заключительная часть
- Задаётся задание на самостоятельное решение:
Т.И.Трофимова «Сборник задач по курсу физики.»
№4.122; 4.127; 4.131;4.136; 4.148; 4.156.
|
|
|




