 |
Тема 2.3 Закон сохранения энергии в механике. Работа. Мощность.
|
|
|
|
I. Цель практического занятия:
1. Закрепить и углубить знания теоретических вопросов, основных понятий и формул, закона сохранения и превращения энергии в механике.
2. Учится применять полученные данные для решения задач по заданной теме.
II. Расчёт учебного времени:
| Содержание занятия: | Время (мин.) |
Вступительная часть:
Объявление темы и цели занятия
Контрольный опрос:
|
Контрольный опрос:
- Работа:
а) Постоянной силы:  ,
, 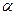 -угол между силой и перемещением.
-угол между силой и перемещением.
б) Переменной силы: 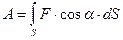
- Мощность:
а) Средняя мощность за  :
: 
б) Мгновенная мощность: 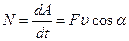 .
.
- Энергия тела:
- Кинетическая:

- Потенциальная энергия тела, поднятого на высоту h над Землёй:
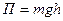
- Потенциальная энергия упругодеформированного тела:
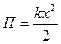
- Для консервативных механических систем:
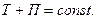
- Работа внешних сил связана с изменением кинетической энергии тела:

Основная часть:
Пример№1 Тр.№1.82
Автомашина массой =1,8 т движется в гору, уклон которой составляет 3м на каждые 100м пути. Определить: 1) работу, совершаемую двигателем автомашины на пути 5 км, если коэффициент трения равен 0,1; 2) развиваемую двигателем мощность, если известно, что этот путь был преодолён за 5 мин.
|
|
|
Дано:
m=1,8∙103кг
h=3 м
S/=100 м
S=5000 м
t=300 с
 =0,1 =0,1
| Решение:
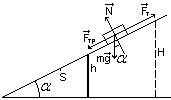 Работа двигателя расходуется на увеличение
потенциальной энергии машины и работу против сил
трения
Работа двигателя расходуется на увеличение
потенциальной энергии машины и работу против сил
трения  : :
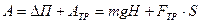 По условию
По условию 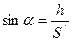 , тогда , тогда 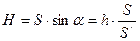 ,
где Н -высота, на которую поднимается машина над землёй: ,
где Н -высота, на которую поднимается машина над землёй:
 Тогда: Тогда: 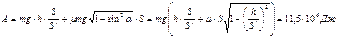 По определению
По определению 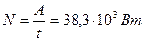
|
| A-? N-? |
Пример№2 Тр.№1.88
Материальная точка массой 1 кг двигалась под действием некоторой силы согласно уравнению S=A-Bt+Ct2-Dt3 (В= 3 м/с, С= 5 м/с2, D= 1 м/с3 ). Определить мощность N, затрачиваемую на движение точки в момент времени t =1с.
| Дано: m =1кг S=A-Bt+Ct2-Dt3 B =3 м/с С =5 м/с2 D =1 м/с3 t =1с | Решение:
По определению мгновенная мощность: 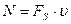
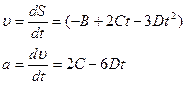 По второму закону Ньютона:
По второму закону Ньютона: 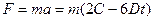 Тогда:
Тогда: 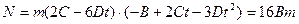
|
| N -? |
Пример№3 Тр.№1.91
Тело массой m начинает двигаться под действием силы 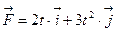 , где
, где 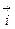 и
и  - соответственно единичные векторы координатных осей x и y. Определить мощность N(t), развиваемую силой в момент времени t.
- соответственно единичные векторы координатных осей x и y. Определить мощность N(t), развиваемую силой в момент времени t.
Дано:
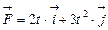
| Решение:
По второму закону Ньютона:
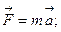  Так как
Так как 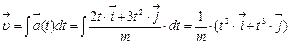 Мгновенная мощность – скалярное произведение векторов
Мгновенная мощность – скалярное произведение векторов  и и 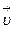 : :
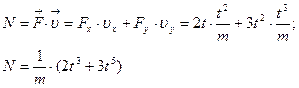
|
| N(t)-? |
Пример№4 Тр.№1.99
Тележка проходит расстояние S=300 м под гору с уклоном  5° и продолжает двигаться в гору с тем же уклоном. Принимая коэффициент трения
5° и продолжает двигаться в гору с тем же уклоном. Принимая коэффициент трения  постоянным и равным 0,05, определить расстояние x, на которое поднимается тележка.
постоянным и равным 0,05, определить расстояние x, на которое поднимается тележка.
Дано:
S=300м
 5° 5°

| Решение:
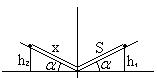 Потенциальная энергия в начальный момент (mgh1)затрачивается на работу против трения и потенциальную энергию подъёма (mgh2):
Потенциальная энергия в начальный момент (mgh1)затрачивается на работу против трения и потенциальную энергию подъёма (mgh2):
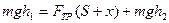 Где
Где 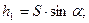 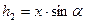 При движении тела по наклонной плоскости:
При движении тела по наклонной плоскости: 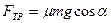 Поэтому:
Поэтому:

|
| x-? |
Пример№5 Тр.№1.107
Шайба массой m скользит без трения с высоты h по желобу, переходящему в петлю радиусом R. Определить: 1) силу давления F шайбы на опору в точке, определяемой углом 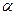 ; 2) угол
; 2) угол 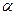 , при котором произойдёт отрыв шайбы.
, при котором произойдёт отрыв шайбы.
| Дано: m, R, h | Решение:
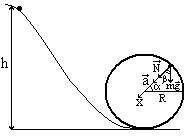 1.Второй закон Ньютона в проекции на нормаль к траектории шайбы в указанной точке:
1.Второй закон Ньютона в проекции на нормаль к траектории шайбы в указанной точке: 
 , ,  По третьему закону Ньютона:
По третьему закону Ньютона: 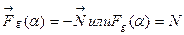 Тогда:
Тогда: 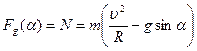 Сила трения отсутствует, поэтому применим закон сохранения энергии:
Сила трения отсутствует, поэтому применим закон сохранения энергии:  Найдём скорость в точке, соответствующей углу Найдём скорость в точке, соответствующей углу  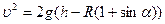 Тогда:
Тогда: 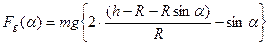 2.Отрыв произойдёт, когда
2.Отрыв произойдёт, когда  
|
F2 -?
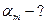
|
|
|
|
Пример№6 Тр.№1.116
Пуля массой m =12 г, летящая с горизонтальной скоростью
 =0,6 км/с, попадает в мешок с песком массой М =10 кг, висящий на длинной нити, и застревает в нём. Определить: 1)высоту, на которую поднимается мешок, отклонившись после удара; 2)долю кинетической энергии, израсходованную на пробивание песка.
=0,6 км/с, попадает в мешок с песком массой М =10 кг, висящий на длинной нити, и застревает в нём. Определить: 1)высоту, на которую поднимается мешок, отклонившись после удара; 2)долю кинетической энергии, израсходованную на пробивание песка.
Дано:
m =0,012кг
 =600м/с
М =10кг =600м/с
М =10кг
| Решение:
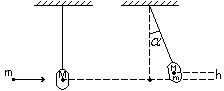 1. Пуля застревает в мешке (неупругий удар), поэтому
применим закон сохранения импульса:
1. Пуля застревает в мешке (неупругий удар), поэтому
применим закон сохранения импульса: 
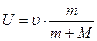 - скорость мешка вместе с пулей после
удара.
Для мешка вместе с пулей применим закон сохранения
энергии: За нулевой уровень потенциальной энергии примем
центр масс мешка до попадания пули: - скорость мешка вместе с пулей после
удара.
Для мешка вместе с пулей применим закон сохранения
энергии: За нулевой уровень потенциальной энергии примем
центр масс мешка до попадания пули:
 Тогда:
Тогда:  2. Доля энергии, израсходованной на пробивание песка:
2. Доля энергии, израсходованной на пробивание песка:
 где
где 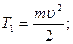 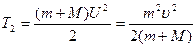
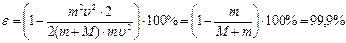
|
h -?
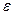 -? -?
|
Пример№7 Чер.2-78
Абсолютно упругий шар массой m =1,8 кг сталкивается с покоящимся упругим шаром большей массы М. В результате прямого удара шар потерял 36% своей кинетической энергии Т1. Определить массу большего шара.
Дано:
m =1,8кг
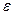 =0.36 =0.36
| Решение:
Так как удар упругий, то:
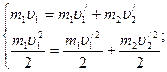 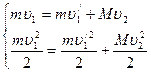 Из первого уравнения:
Из первого уравнения: 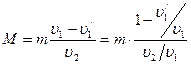 Распишем потерю кинетической энергии первым шаром:
Распишем потерю кинетической энергии первым шаром:
 , то , то 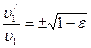 С другой стороны:
С другой стороны: 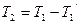 , тогда: , тогда: 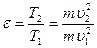 . Тогда: . Тогда: 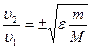 Так как
Так как 
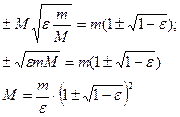 Так как M>m, то
Так как M>m, то 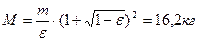
|
| M -? |
Пример№8 Чер.5-17
Пружина жёсткостью k =10 кН/м сжата силой F =200 Н. Определить работу внешней силы, дополнительно сжимающей эту пружину ещё на 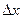 =1 см.
=1 см.
Дано:
k =104 н/м
F =200н
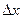 =0,01м =0,01м
| Решение:
Пусть сила, сжимающая пружину:
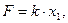 где x1- первоначальная деформация пружины.
Тогда работа силы, дополнительно сжимающей пружину: где x1- первоначальная деформация пружины.
Тогда работа силы, дополнительно сжимающей пружину:
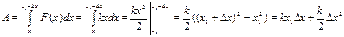 Так как
Так как 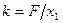 , то: , то: 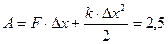 Дж Дж
|
| А -? |
Пример№9 Чер.4-26
Определить работу А, которую совершат силы гравитационного поля Земли, если тело массой m =1кг упадёт на поверхность Земли: 1) с высоты h, равной радиусу R Земли; 2) из бесконечности.
Дано:
m =1кг
h1 =R3
h2 = 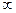
| Решение:
1. 
 МЖд
2. МЖд
2.  =G =G 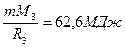
|
| A1 -? A2 -? |
Заключительная часть:
Задание на самостоятельное решение:
Т.И.Трофимова «Сборник задач по курсу физики»:
№1.83; №1.93; №1.98: №1.101; 1.102; 1.110; 1.112; 1.124.
|
|
|


