1. Постановка задачи оптимального управления

МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

 

1. Постановка задачи оптимального управления

1. 1. Задача оптимального управления.

Оптимальным называется управление, обеспечивающее достижение наилучших, в смысле выбранного критерия, показателей качества системы в условиях заданных ограничений на управляющие воздействия и переменные состояния.

Важнейшую роль в проблемах оптимального управления играет корректная постановка задачи, то есть адекватный выбор критерия оптимальности и ограничений.

В большинстве случаев перевести объект управления из одного состояние в другое (из исходного в заданное) можно множеством способов. Эти способы реализуются с помощью различных законов управления. Задача оптимального управления заключается в выборе из множества управлений такой закон, чтобы процесс перехода объекта управления из исходного состояния в заданное был оптимальным по определенному критерию (критерию оптимальности). В качестве критерия может использоваться, например, количество энергии, затрачиваемой на процесс перехода, или время, затраченное на переход.

 

1. 2. Формализация задачи оптимального управления.

1. 2. 1. Математическая модель объекта управления.

Математическая модель объекта управления (ОУ) задается системой уравнений

                                                         (1)

где:   - вектор состояния, координатами которого являются состояния (фазовые координаты) ОУ;

    - вектор управления ( ), координатами которого являются управляющие воздействия на ОУ, создаваемые регулирующими органами ОУ;

   t – время, 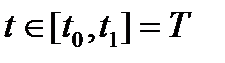 - период функционирования системы;

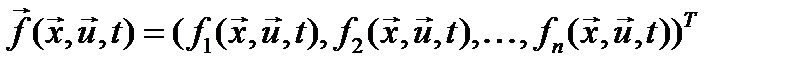   - заданная вектор – функция, конкретный вид которой определяется конструктивными или физическими особенностями объекта управления. Предполагается, что все функции  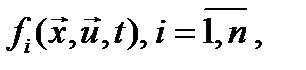непрерывны вместе со своими частными производными по всей совокупности переменных.

На состояния и управления могут быть наложены ограничения.

Под состояниями  понимаются изменяемые во времени внутренние параметры ОУ, значения которых характеризуют состояние ОУ в каждый момент времени t.

Состояние объекта в каждый момент времени можно изобразить точкой в n – мерном пространстве Rⁿ, называемым пространством состояний ОУ. Движение объекта в пространстве состояний проявляется в том, что координаты вектора 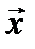 меняются с течением времени t. При движении объекта в пространстве состояний точка  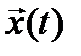описывает в пространстве состояний траекторию.

Пусть S – множество значений состояний, в которых объект может находиться (ограничения на состояния могут быть связаны, например, с максимально допустимым давлением, температурой и т. п. ). Обычно эти ограничения задаются неравенствами 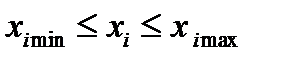 . В этом случае множество S геометрически представляет из себя гиперпараллелепипед в пространстве Rⁿ.

При наличии ограничений вектор состояний объекта 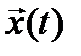в каждый момент времени должен удовлетворять условию

                                                      (2)

Условие (2) называется ограничением на состояния.

Вектор  определяет точку в k - мерном пространстве . В пространстве  выделяется множество U, называемое множеством допустимых управлений. В любой момент времени точка должна принадлежать этому множеству.

                                                          (3)

Условие (3) называется ограничением на управление.

Объект, математическая модель которого описывается системой уравнений (1), является управляемым, что выражается в следующем: если выбрано некоторое допустимое управление , , 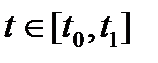то подстановка его в (1) приводит к системе обыкновенных дифференциальных уравнений (ОДУ) в векторной форме

 .                                                      (4)

При заданных начальных условиях 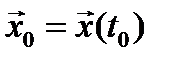 получаем задачу Коши, которая при условии непрерывности функции  вместе с ее производными имеет единственное решение.

Решение системы ОДУ (4) с заданными начальными условиями   называется фазовой траекторией, соответствующей заданному управлению.

Начальное условие  в задачах оптимального управления часто называют начальным состоянием.

Если 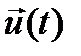 - допустимое управление, 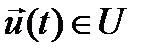,  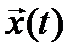- траектория, удовлетворяющая ограничению (2),  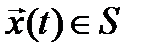, то пара функций  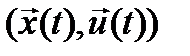называется допустимым процессом.

При рассмотрении реальных управляемых объектов прежде всего возникает задача управления.

Пусть задано множество М (цель управления) тех состояний, которые являются желательными. При этом должно выполняться условие .

Если управление 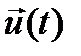, , 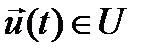переводит объект (1) из начального состояния  в некоторое состояние  за время 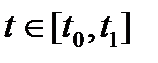 (t₁, вообще говоря, может быть заранее неизвестно), то будем говорить, что управление  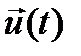реализует цель управления М.

Задача управления объектом состоит в том, чтобы найти допустимое управление 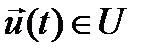, реализующее заданную цель управления.

 

123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: