1.2.2. Краевые условия. 1.2.3. Критерий оптимальности.. 1.2.4. Интегральные критерии оптимальности.

1. 2. 2. Краевые условия.

Если множество М, характеризующее цель управления, совпадает со всем пространством состояний , то такую задачу называют задачей со свободным концом траектории. В этом случае краевым является начальное условие .

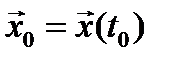Более сложными являются так называемые двухточечные задачи.

Задача с фиксированными концами. Краевые условия в этом случае имеют вид 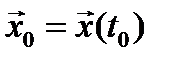 и 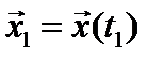. При этом интервал времени (t₁ – t₀) может быть как заданным, так и подлежащим определению. (При t₀ = 0 может быть заданным или подлежащим определению время t₁ – момент окончания процесса управления). В этом случае множество М (цель управления) состоит из единственной точки .

Задача с подвижными концами. Требуется перевести объект из состояния , принадлежащего некоторому заданному множеству  в некоторое состояние , принадлежащего некоторому заданному множеству . Множества М₀ и М₁ представляют собой гиперповерхности в пространстве состояний Rⁿ. Если М₀ и М₁ вырождаются в точки, то получаем задачу с фиксированными концами.

 

1. 2. 3. Критерий оптимальности.

Допустимых управлений, реализующих цель управления, может быть бесконечно много. В таком случае ставится задача оптимального выбора: из всех допустимых управлений выбрать такое, при котором процесс управления будет наилучшим. То есть если качество процесса оценивается некоторой числовой характеристикой I (в качестве такой характеристики можно выбрать, например, время регулирования или запас устойчивости по амплитуде), то задача, чтобы выбором управления обеспечить ее максимальное или минимальное значение. Эту числовую характеристику называют критерием оптимальности.

Значения критерия оптимальности зависят от управления  и динамики управляемого процесса, описываемой вектором состояний . Критерий качества в этом случае можно рассматривать как функцию, аргументами которой являются другие функции, . В математике такие функции называются функционалами.

Задача оптимального управления состоит в отыскании управления, обеспечивающего минимум или максимум этого функционала. Случай, когда требуется максимизировать функционал, сводится к задаче минимизации заменой исходного функционала I на – I, поэтому случай максимизации отдельно не рассматривается.

Таким образом, задача оптимального управления состоит в том, чтобы найти такое управление , реализующее цель управления, при котором функционал принимает наименьшее значение. При этом  называется оптимальным управлением, соответствующая траектория  - оптимальной траекторией, а процесс ( , ) – оптимальным процессом.

 

1. 2. 4. Интегральные критерии оптимальности.

Для объектов управления, описываемых уравнением (1), наиболее широко используются в качестве критериев оптимальности функционалы вида

 .

К этому классу критериев относятся:

а). Критерий минимального быстродействия с подынтегральной функцией

, т. е.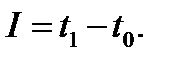  

Оптимальное управление в задачах с критерием минимального быстродействия называется управлением, оптимальным по быстродействию.

б). Интегральный квадратичный критерий с подынтегральной функцией

 

где - вектор состояния, а среди коэффициентов  есть хотя бы один, отличный от нуля. Может рассматриваться как конечный , так и бесконечный 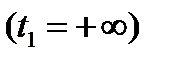интервал времени. Такой критерий дает косвенное представление о точности работы системы.

в). Интегральные энергетические критерии оптимальности с подынтегральными функциями

 или ,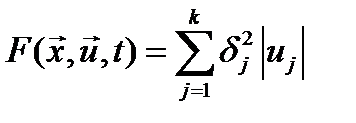

где - вектор управления, а среди коэффициентов  есть хотя бы один, отличный от нуля.

Эти критерии характеризуют затраты энергии, например в задачах управления космическими объектами с помощью ЖРД.

г). Смешанный интегральный критерий с подынтегральный функцией

.

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: