 |
2.3. Вариации функционала. 2.4. Необходимое условие экстремума функционала
|
|
|
|
2. 3. Вариации функционала
Если приращение функционала можно представить в виде
где 
- линейный относительно 
функционал, 
- максимальное значение 
и 
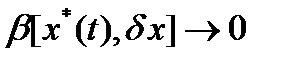при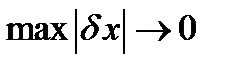 
, то линейная по отношению к 
часть функционала 
называется первой вариацией функционала.
Можно дать и другое определение первой вариации функционала, используя представление функции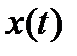 
с использованием формулы (14):
. (15)
В формуле (15) вариация функции представлена как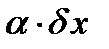 
, где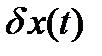 
- фиксированная функция, а a - числовой параметр (переменная величина).
При таком представлении вариации функции выражение 
является функцией 
числового параметра a, поэтому ее можно разложить в ряд Тейлора по степеням a в окрестности точки a = 0:
где: 
- первая вариация функционала,
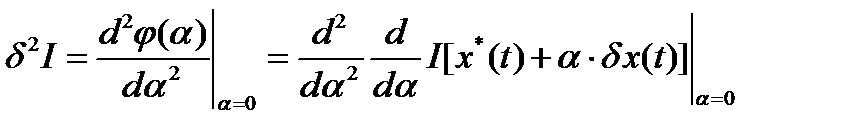- вторая вариация функционала.
Замечание. В литературе часто вместо обозначения 
используют обозначение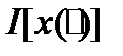 
, чтобы отличать элемент 
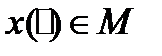(то есть функцию, являющуюся точкой в некотором пространстве М) от значения функции 
при фиксированном значении t (в этом случае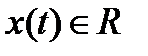 
).
Пример. Найти первую вариацию функционала
Первый способ.
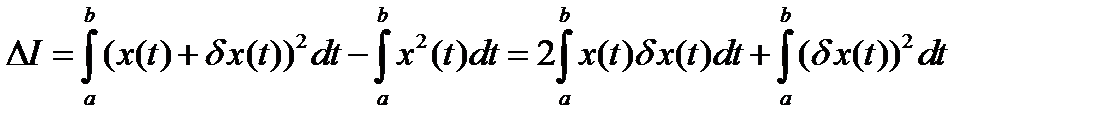(16)
Для второго слагаемого в формуле (16) можно получить оценку сверху
. (17)
Подставляя (17) в формулу (16), получаем:
, (18)
где 
а первое слагаемое в формуле (18) линейно по 
, следовательно, по определению первая вариация функционала равна
. (19)
Второй способ.
В соответствии со вторым определением, первая вариация функционала равна
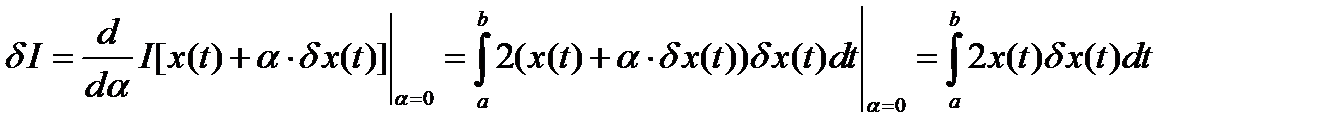(20)
Сравнение (19) и (20) показывает, что оба способа вычисления первой вариации функционала дают одинаковый результат.
|
|
|
2. 4. Необходимое условие экстремума функционала
Различают сильный и слабый локальный минимум (максимум) функционала.
Говорят, что функционал 
достигает на кривой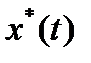 
сильного минимума (максимума), если 
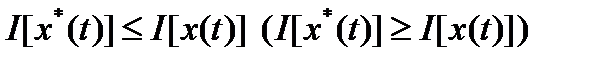в сильной e - окрестности кривой .
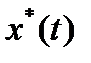Говорят, что функционал достигает на кривой 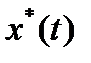слабого минимума (максимума), если 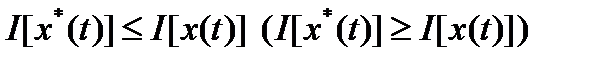в слабой e - окрестности кривой .
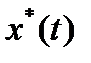Замечание. Всякий сильный экстремум функционала является и слабым. Обратное, вообще говоря, неверно.
Необходимое условие экстремума функционала.
Если функционал , имеющий вариацию, достигает минимума или максимума на кривой 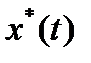, где 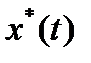есть внутренняя точка области определения функционала, то при 
первая вариация функционала равна нулю: 
.
Замечание. Различие между сильным и слабым экстремумом не имеет существенного значения при выводе достаточного условия экстремума, но весьма существенно при выводе и применении достаточных условий экстремума.
При выводе достаточных условий экстремума функционала для различных постановок вариационных задач применяется следующая важная лемма.
Основная лемма вариационного исчисления.
Если для каждой непрерывной функции 
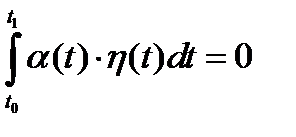, (21)
где функция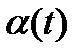 
непрерывна на отрезке 
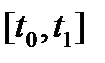, то 
на том же отрезке.
Замечание. Утверждение основной леммы вариационного исчисления не изменится, если на функцию наложить следующие дополнительные ограничения: имеет непрерывную на отрезке 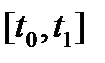производную и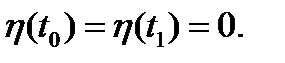 
Рассмотрим необходимое условие экстремума для интегрального функционала вида
, (22)
где функция 
непрерывна вместе со своими первыми частными производными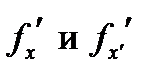 
.
Первая вариация функционала, вычисленная по второму способу (см. п. 2. 3), будет определяться формулой:
|
|
|
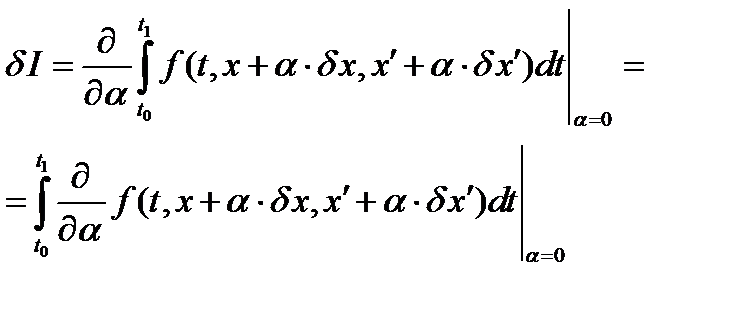. (23)
Для вычисления частной производной под знаком интеграла введем переменные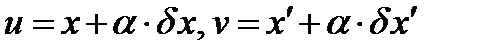 
. Тогда
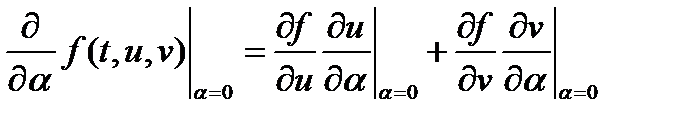. (24)
Учитывая, что при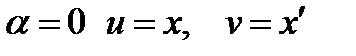 
, из (23) с учетом (24) получаем
(25)
Таким образом, необходимое условие экстремума функционала (22) имеет вид
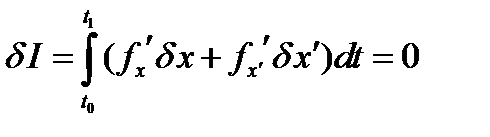. (26)
|
|
|
