 |
3. Оптимальное управление детерминированными системами
|
|
|
|
3. Оптимальное управление детерминированными системами
3. 1. Нахождение оптимального программного управления.
Под системой автоматического управления будем понимать (согласно ТАУ) совокупность объекта управления и управляющего устройства. Управляющее устройство вырабатывает управляющее воздействие, которое преобразуется объектом управления (ОУ) в выходной сигнал. Управление и выходной сигнал являются векторными величинами, т. е. в каждый момент времени они представлены вектором управления 
и вектором выхода 
.
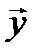В общем случае вектор выхода связан с вектором состояния 
уравнением выхода 
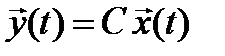, где С – матрица выхода. Будем считать, что вектор выхода совпадает с вектором состояния, т. е. С = Е. При этом предположении объект управления будет описываться только уравнением состояния 
, где А – матрица системы, В – матрица управления.
Управление, действующее на ОУ, может зависеть:
a) только от времени (разомкнутая АС). В этом случае результат функционирования системы не влияет на процесс управления, а управление называется программным;
b) от времени и от всех координат вектора состояния. При этом управление зависит от результата функционирования объекта и называется управлением с полной обратной связью;
c) от времени и части координат вектора состояния, доступных измерению. Такое управление называется управлением с неполной обратной связью.
3. 1. 1. Постановка задачи нахождения оптимального программного управления
Предполагается, что при управлении используется информация только о времени, т. е. система является разомкнутой по состоянию и реализуется программное управление:
| УУ |
| ОУ |
|
|
|
|
|
Постановка задачи оптимального управления включает в себя:
- математическую модель ОУ в виде обыкновенного дифференциального уравнения первого порядка;
- цель управления (критерий оптимальности, количественно характеризующий качество управления), в виде функционала;
- различные ограничения на допустимые управления, допустимые траектории системы в пространстве состояний, длительность процесса управления и т. д.
3. 1. 2. Формальная постановка задачи нахождения оптимального управления
Заданы:
а). Математическая модель ОУ
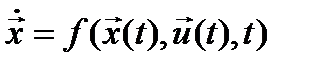(1)
где: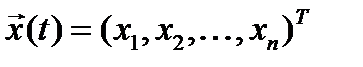 
- вектор состояния системы, 
;
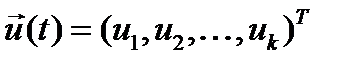- вектор управления, 
, U – заданное множество допустимых управлений;
- непрерывная вместе со своими частными производными вектор-функция, 
- n-мерное евклидово пространство.
t – время,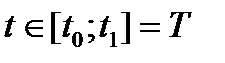 
- интервал времени функционирования системы.
Момент начала процесса t0 задан, а момент окончания процесса t1 или задан, или определяется первым моментом достижения точкой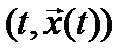 
некоторой заданной гиперповерхности 
,
,
т. е. в момент времени t1 должно выполняться условие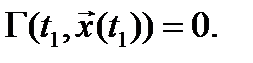 
b). Функционал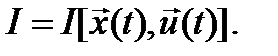 
Требуется определить вектор функции 
доставляющие минимум заданному функционалу при переводе системы из начального состояния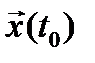 
в конечное состояние 
.
3. 1. 3. Классификация задач оптимального управления
Задачи оптимального управления классифицируются:
- по способу задания функционала;
- по способу задания ограничений вдоль траектории;
- по способу заданий краевых условий.
Классификация по способу задания функционала.
Функционал качества управления:
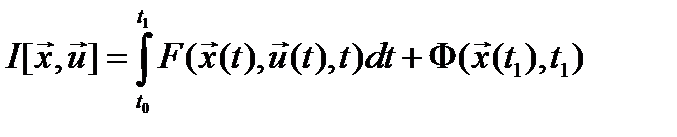(2)
где: 
- заданные функции,
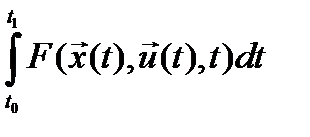- интегральный член,
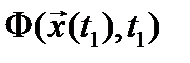- терминальный член.
Требуется найти минимум функционала
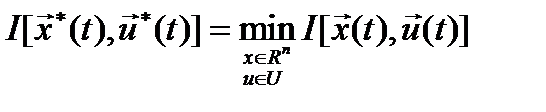(3)
|
|
|
Задача (3) с функционалом (2) называется задачей Больца.
Если в функционале (2) функция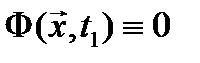 
(отсутствует терминальный член), то задача (3) называется задачей Лагранжа.
Если в функционале (2) функция 
(отсутствует интегральный член), то это задача Майера.
Искомые функции 
называются оптимальной траекторией и оптимальным управлением.
Классификация по способу задания ограничений:
- ограничения на управление, например 
- ограничения на траектории, например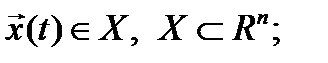 
- ограничения в виде равенств 
или неравенств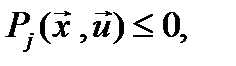 
где 
- интегральные ограничения (изопериметрическая задача)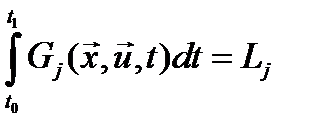 
, где Gj - скалярные функции, Lj – числа.
Классификация по способу задания краевых условий:
- задача с фиксированными концами, когда 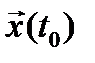и заданы;
- задача со свободным концом, когда 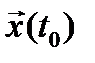или не заданы;
- задача с подвижными концами, когда t1 фиксировано, а 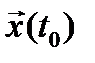и принадлежат некоторым заданным гиперповерхностям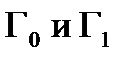 
.
Первые два случая подразделяются на задачи с фиксированным и нефиксированным временем окончания процесса t1.
|
|
|
