 |
3.2.3. Алгоритм поиска оптимального управления с полной обратной связью.
|
|
|
|
3. 2. 3. Алгоритм поиска оптимального управления с полной обратной связью.
1. Записать уравнение Беллмана (5) с граничным условием.
2. Найти структуру оптимального управления с полной обратной связью, исходя из условия максимума (6) по управлению. Искомое управление 
обычно выражается через производные функции 
.
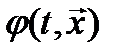3. Подставить полученное выражение для управления в уравнение (5). Нахождение искомого оптимального управления сводится к решению нелинейного дифференциального уравнения с частными производными первого порядка.
4. Найти решение полученного уравнения и явный вид искомого управления.
Пример.
Дано:
- модель объекта управления
;
где 
- функционал
Требуется найти оптимальное управление с полной обратной связью .
По виду функционала это задача Больца.
В принятых выше обозначениях 
Решение по алгоритму.
1. Записываем уравнение Беллмана и граничные условия
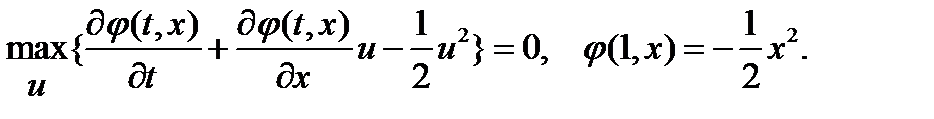
2. Находим структуру оптимального управления из условия максимума по управлению выражения в фигурных скобках, то есть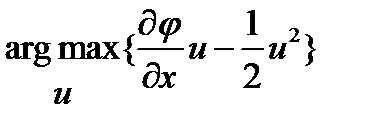 
:
.
3. Подставляем полученное выражение для управления в уравнение Беллмана
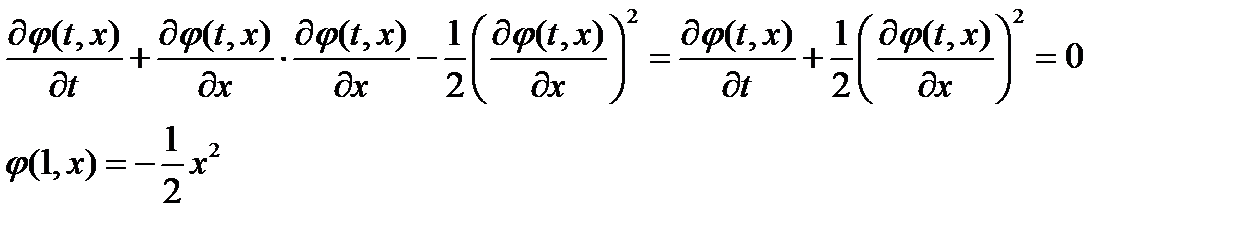
4. Ищем решение полученного уравнения в частных производных в виде 
(см. граничное условие в п. 3), где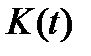 
- неизвестная функция. Подставляем выражение для 
в п. 3:
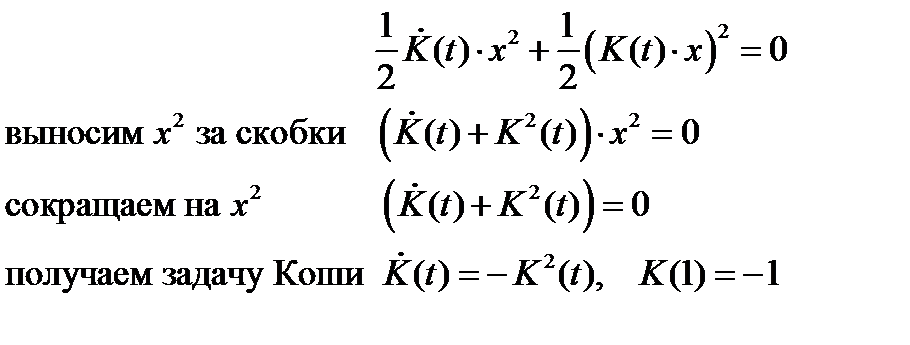
Граничное условие в задаче Коши получено с учетом п. 3 и п. 4: 
.
Полученное в задаче Коши ОДУ является уравнением с разделяющимися переменными. Найдем его решение аналитически:
.
Постоянную интегрирования С находим из граничного условия
.
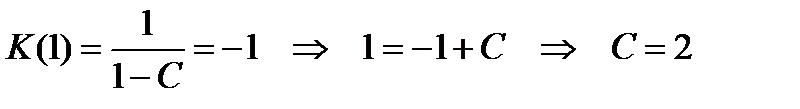Искомое решение 
Решение задачи Коши в Matlab:
|
|
|
Искомое оптимальное управление с полной обратной связью
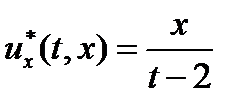. (7)
Найдем оптимальную траекторию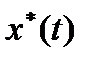 
и оптимальное управление 
.
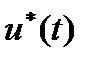Модель объекта управления , подставляя (7), получаем:
.
Получили задачу Коши. ОДУ с разделяющимися переменными.
Решаем уравнение, разделяя переменные:
Постоянную интегрирования С находим из начального условия:
.
Оптимальная траектория 
. (8)
Оптимальное управление 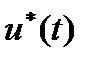получаем из формулы (7) подстановкой оптимальной траектории 
: 
Оптимальное управление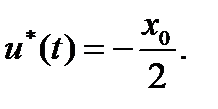 
(9)
Если применить для решения вышеприведенной задачи принцип максимума Понтрягина, рассмотренный на предыдущей лекции, то мы получим ту же оптимальную траекторию (8) и то же оптимальное управление (9). Но уравнение Беллмана позволяет дополнительно определить уравнение оптимального регулятора с полной обратной связью (7), то есть решить задачу синтеза оптимального регулятора в системе с полной обратной связью.
|
|
|
