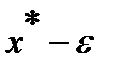|
1.2.5. Терминальные функционалы.
|
|
|
|
1. 2. 5. Терминальные функционалы.
В теории оптимального управления часто встречаются терминальные функционалы вида
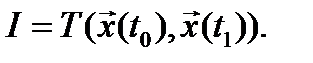
К этому классу неинтегральных критериев оптимальности относится, например, критерий конечного состояния 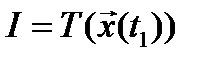 . Его обычно используют в тех случаях, когда требуется перевести систему в заданное конечное состояние
. Его обычно используют в тех случаях, когда требуется перевести систему в заданное конечное состояние  в момент времени t1 с наименьшей ошибкой. В такой постановке задачи критерий имеет вид
в момент времени t1 с наименьшей ошибкой. В такой постановке задачи критерий имеет вид
 .
.
Анализ приведенной выше постановки задачи оптимального управления показывает, что для ее решения необходимо минимизировать функционал, аргументами которых являются неизвестные функции. Методы решения таких задач рассматриваются в разделе высшей математики, который называется «Вариационное исчисление».
2. Основы вариационного исчисления
2. 1. Задачи, приводящие к решению экстремальных проблем
| О |
| yb |
| b |
| у |
| х |
| В |
| Рис. 1. Брахистотрона |
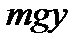 , где
, где  - масса точки,
- масса точки,  - ускорение свободного падения. Кинетическая энергия при этом увеличится на
- ускорение свободного падения. Кинетическая энергия при этом увеличится на  , где
, где 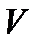 - скорость точки.
- скорость точки. |
|
|
В силу закона сохранения энергии
 ,
,
откуда скорость точки 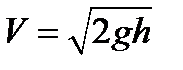 .
.
Предполагая, что траектория движения есть кривая, описываемая уравнением 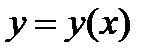 , причем
, причем  - гладкая функция, определенная на отрезке
- гладкая функция, определенная на отрезке  , получаем
, получаем
 , (5)
, (5)
где: 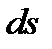 - дифференциал дуги кривой;
- дифференциал дуги кривой;
t – время.
Равенство (5) можно переписать в виде
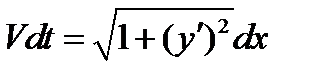 ,
,
откуда  . (6)
. (6)
Используя уравнение (6), можно найти время, необходимое для перехода из точки О в точку В:
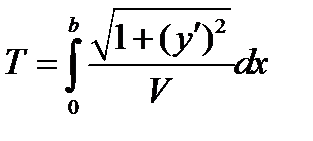 . (7)
. (7)
Краевые условия
 . (8)
. (8)
Требуется найти гладкую функцию  , доставляющую минимум интегралу (7) при краевых условиях (8).
, доставляющую минимум интегралу (7) при краевых условиях (8).
Задача о брахистотроне была сформулирована Иоганном Бернулли в 1696 году, поэтому1696 год принято считать датой рождения вариационного исчисления как раздела математики.
2. 2. Основные определения
Пусть задано некоторое множество функций М.
Функционалом I на множестве М называется отображение 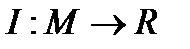 множества функций М на множество действительных чисел R.
множества функций М на множество действительных чисел R.
То есть функционал – это функция, аргументами которой являются функции, принадлежащие некоторому множеству М (М – область определения функционала, если  , то f - допустимая функция), областью значений функционала является множество действительных чисел. Т. е. функционал – это функция, аргументами которой являются функции, принадлежащие некоторому множеству М (М – область определения функционала, если
, то f - допустимая функция), областью значений функционала является множество действительных чисел. Т. е. функционал – это функция, аргументами которой являются функции, принадлежащие некоторому множеству М (М – область определения функционала, если 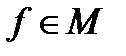 , то
, то  - допустимая функция), а областью значений функционала является множество действительных чисел.
- допустимая функция), а областью значений функционала является множество действительных чисел.
Множество М – нормированное пространство. Норма элемента 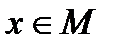 обозначается
обозначается  .
.
Нормой элемента 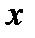 , принадлежащего некоторому пространству, называется вычисляемое по определенному правилу неотрицательное число, удовлетворяющее следующим свойствам:
, принадлежащего некоторому пространству, называется вычисляемое по определенному правилу неотрицательное число, удовлетворяющее следующим свойствам:
|
|
|
1).  ≥ 0,
≥ 0,  = 0 тогда и только тогда, когда x = 0.
= 0 тогда и только тогда, когда x = 0.
2).  , где
, где  - число.
- число.
3). 
Примеры норм:
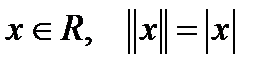
 - евклидова норма. (9)
- евклидова норма. (9)
Пространство  с заданной на нем нормой (9) называется евклидовым пространством.
с заданной на нем нормой (9) называется евклидовым пространством.
Если М – множество функций  , непрерывных на отрезке
, непрерывных на отрезке  то для любой функции
то для любой функции 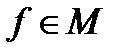 норма определяется формулой
норма определяется формулой
 - банахова норма. (10)
- банахова норма. (10)
Если на множестве М функций, непрерывных на  задана банахова норма (10), то М – банахово пространство
задана банахова норма (10), то М – банахово пространство  .
.
Если М – множество функций, непрерывных вместе со своими первыми производными на  то это банахово пространство
то это банахово пространство  с нормой
с нормой
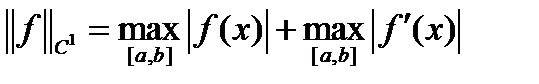 . (11)
. (11)
В общем виде: банахово пространство 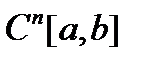 n раз непрерывно дифференцируемых на
n раз непрерывно дифференцируемых на 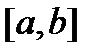 функций имеет норму, определяемую по формуле
функций имеет норму, определяемую по формуле
 . (12)
. (12)
Значение аргумента действительной функции действительного аргумента 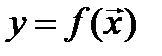 , где
, где 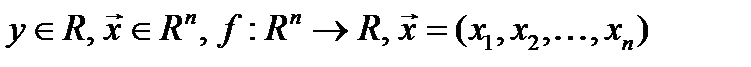 , называют точкой в пространстве
, называют точкой в пространстве 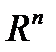 .
.
Расстояние между точками в евклидовом пространстве 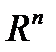 определяется нормой (9)
определяется нормой (9)
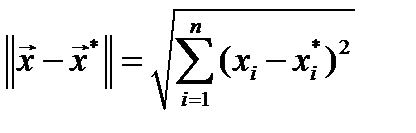 .
.
По аналогии функции, являющиеся аргументами функционала, мы будем называть точками в банаховом пространстве, а расстояния между функциями вычислять по формулам (10), (11) или (12).
Линейным функционалом называется функционал, удовлетворяющий условиям:
 (13)
(13)
Пример:

Пусть задано произвольное положительное число 
Сильной 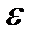 - окрестностью функции
- окрестностью функции  называется множество функций
называется множество функций 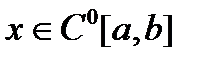 , для которых
, для которых 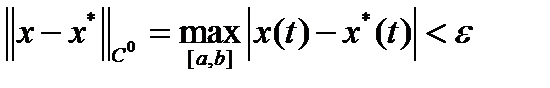 .
.
Слабой 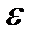 - окрестностью функции
- окрестностью функции  называется множество функций
называется множество функций 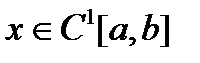 , для которых
, для которых 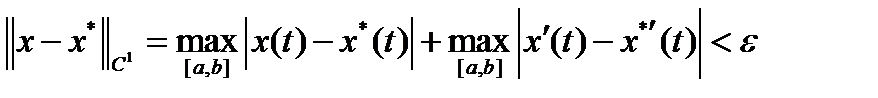 .
.
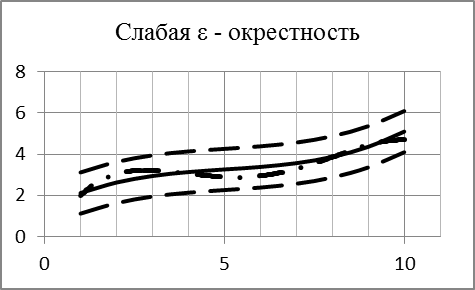
Графическая иллюстрация понятий сильной и слабой 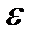 - окрестности функции показана на рисунке 2.
- окрестности функции показана на рисунке 2.

|
|
Рис. 2. e - окрестности функции.
Из определения e - окрестностей ясно, что функция, попадающая в слабую e - окрестность, принадлежит и сильной e - окрестности.
Функционал 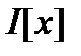 , определенный на нормированном пространстве М, называется непрерывным в точке
, определенный на нормированном пространстве М, называется непрерывным в точке 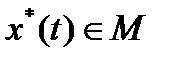 , если
, если
|
|
|
 такое, что
такое, что  .
.
Выберем некоторую функцию 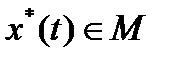 . Пусть
. Пусть 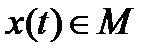 - произвольная функция.
- произвольная функция.
Разность
 (14)
(14)
называется вариацией функции 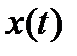 .
.
Отличие вариации функции 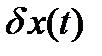 от приращения функции
от приращения функции 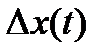 : приращение функции
: приращение функции  есть разность двух значений функции, то есть
есть разность двух значений функции, то есть  - число, а вариация
- число, а вариация 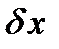 - функция,
- функция, 
Приращением функционала 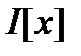 , определенного на нормированном пространстве
, определенного на нормированном пространстве 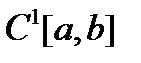 , в точке
, в точке  называется величина, вычисляемая по формуле
называется величина, вычисляемая по формуле
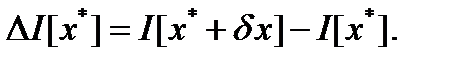
|
|
|