 |
3.2. Нахождение оптимального управления с полной обратной связью
|
|
|
|
3. 2. Нахождение оптимального управления с полной обратной связью
3. 2. 1. Постановка задачи.
Пусть поведение объекта управления описывается системой обыкновенных дифференциальных уравнений (ОДУ)
(1)
где: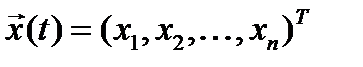 
- вектор состояния системы, 
;
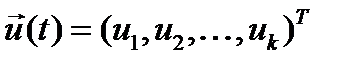- вектор управления, 
, U – заданное множество допустимых управлений;
t – время,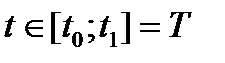 
- интервал времени функционирования системы;
- непрерывная вместе со своими частными производными вектор-функция, 
- n-мерное евклидово пространство,
.
Момент начала процесса t0 задан, а момент окончания процесса t1 или задан, или определяется первым моментом достижения точкой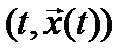 
некоторой заданной гиперповерхности 
,
, (2)
т. е. в момент времени t1 должно выполняться условие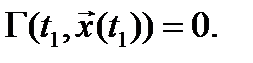 
b). Функционал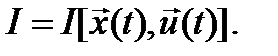 
Требуется определить вектор функции 
доставляющие минимум заданному функционалу при переводе системы из начального состояния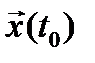 
в конечное состояние 
.
Начальное условие 
заранее не задано и может быть произвольно на множестве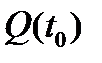 
.
Произвольность начального значения 
понимается в следующем смысле:
Пусть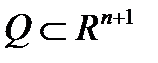 
- множество точек 
, из которых можно достигнуть терминального множества Г по некоторой траектории, соответствующей допустимому управлению. Тогда 
- сечение множества Q при фиксированном t = t0.
Задано множество допустимых управлений U0, элементами которого являются кусочно-непрерывные функции u(t) со значениями в множестве 
.
Задано множество допустимых процессов D, элементами которого являются тройки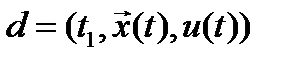 
, которые включают момент окончания процесса, траекторию x(t) и управление u(t), где для любого 
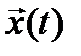непрерывные и кусочно-непрерывно дифференцируемые, u(t) – кусочно-непрерывные, удовлетворяющие уравнению (1) с начальным условием и условию (2).
|
|
|
На множестве допустимых процессов D определен функционал качества управления
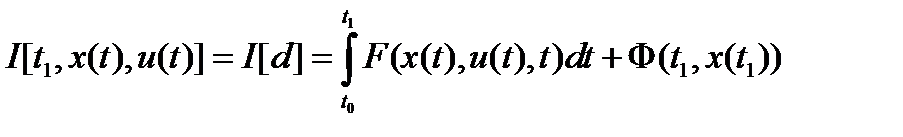(3)
где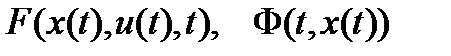 
- заданные непрерывно дифференцируемые функции.
Предполагается, что при управлении используется информация о времени t и всех координатах вектора состояния 
.
Множество допустимых управлений с полной обратной связью Un образуют функции 
которые для каждого начального состояния 
порождают соответствующие тройки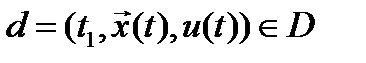 
, в которых программное управление 
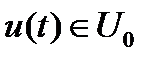, а для любого 
.
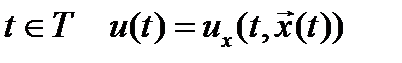Управление с полной обратной связью схематично представлено на рис. 1.
|
|
|
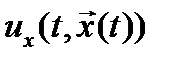
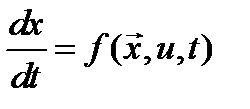
Рис. 1.
Требуется найти такую функцию 
, чтобы функционал (3) на этой функции достигал минимума
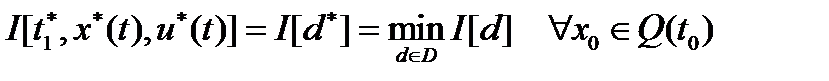(4)
где 
.
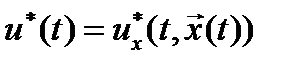Функция 
называется оптимальным управлением с полной обратной связью, а формула, описывающая эту функцию, является уравнением оптимального регулятора в системе с полной обратной связью.
Для любого начального состояния 
функция порождает оптимальную траекторию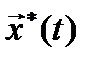 
, оптимальное управление 
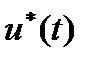и оптимальное время окончания процесса 
.
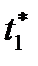3. 2. 2. Достаточные условия оптимальности.
Достаточные условия оптимальности управления с полной обратной связью определяются следующей теоремой.
Теорема. Если существует функция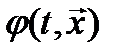 
, удовлетворяющая уравнению Беллмана
(5)
с граничными условиями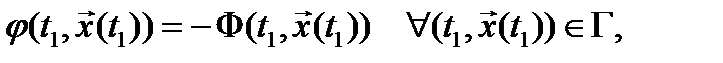 
и управление , удовлетворяющее условию
, (6)
то является оптимальным управлением с полной обратной связью в задаче (4).
При этом минимальное значение функционала равно 
.
Примечание. Аргумент максимизации (argmax или arg max) — значение аргумента, при котором данное выражение достигает максимума. 
argmax x f ( x ) {\displaystyle {\underset {x}{\operatorname {argmax} }}\, f(x)} 
есть значение хx {\displaystyle x}, при котором 
f ( x ) {\displaystyle f(x)} достигает своего наибольшего значения. Является решением задачи 
argmax x f ( x ) ∈ { x | ∀ y: f ( y ) ≤ f ( x ) } {\displaystyle {\underset {x}{\operatorname {argmax} }}\, f(x)\quad \in \quad \{x\ |\ \forall y: f(y)\leq f(x)\}}
|
|
|
Аргумент максимизации определяется единственным образом тогда и только тогда, когда максимум достигается в единственной точке: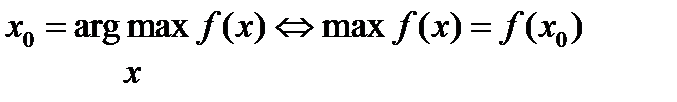 
x 0 = argmax x f ( x ) ⇔ max f ( x ) = f ( x 0 ) {\displaystyle x_{0}={\underset {x}{\operatorname {argmax} }}\, f(x)\Leftrightarrow \max f(x)=f(x_{0})}
Если же максимум достигается в нескольких точках, то argmax может быть расширен до набора решений.
|
|
|
