 |
2.5. Задачи с фиксированными границами.
|
|
|
|
2. 5. Задачи с фиксированными границами.
2. 5. 1. Уравнение Эйлера
Рассмотрим множество М допустимых функций, удовлетворяющих следующим условиям:
- функции 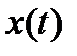 определены и непрерывно дифференцируемы на интервале
определены и непрерывно дифференцируемы на интервале  где
где 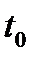 и
и  заданы, т. е.
заданы, т. е. 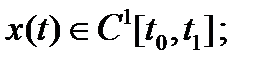
- функции 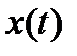 удовлетворяют граничным условиям
удовлетворяют граничным условиям
 (27)
(27)
где значения  и
и  заданы, т. е. кривые проходят через две закрепленные граничные точки.
заданы, т. е. кривые проходят через две закрепленные граничные точки.
На множестве М задан функционал
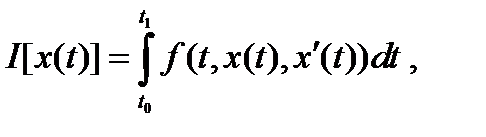 (28)
(28)
где подынтегральная функция 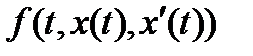 имеет непрерывные частные производные до второго порядка включительно по всем переменным.
имеет непрерывные частные производные до второго порядка включительно по всем переменным.
Среди допустимых функций (кривых) 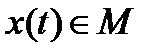 требуется найти функцию (кривую)
требуется найти функцию (кривую) 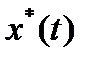 , на которой функционал (28) достигает экстремума, т. е.
, на которой функционал (28) достигает экстремума, т. е.
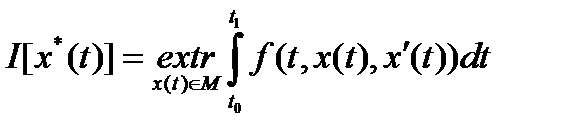 (29)
(29)
и на кривые 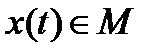 не наложены никакие дополнительные условия, кроме граничных условий (27).
не наложены никакие дополнительные условия, кроме граничных условий (27).
Поскольку в граничных точках функции x(t) принимают фиксированные значения, вариации функций в граничных точках равны нулю:
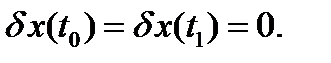 (30)
(30)
Первая вариация функционала (28) определяется полученной ранее формулой (25), которую можно разложить на сумму двух интегралов:
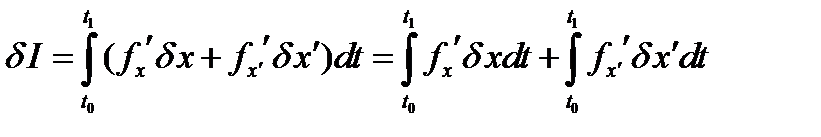 . (31)
. (31)
Проинтегрируем второй интеграл в формуле (31), используя правило интегрирования по частям 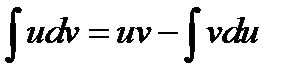 .
.
Обозначим  , тогда
, тогда
 . (32)
. (32)
Подставляя полученный результат в (31) с учетом (30) получаем
 (33)
(33)
Необходимое условие экстремума функционала 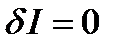 , откуда
, откуда
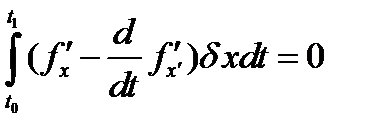 . (34)
. (34)
|
|
|
В уравнении (34) вариация 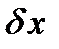 - произвольная непрерывная на
- произвольная непрерывная на  функция, поэтому согласно основной лемме вариационного исчисления из (34) следует
функция, поэтому согласно основной лемме вариационного исчисления из (34) следует
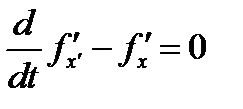 (35)
(35)
Уравнение (35) называется уравнением Эйлера для функционала и является необходимым условием экстремума функционала (28) с граничными условиями (27). Функции  , удовлетворяющие уравнению (35), называются экстремалями функционала.
, удовлетворяющие уравнению (35), называются экстремалями функционала.
2. 5. 2. Простейшие случаи интегрируемости уравнения Эйлера
a. Функция 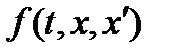 не зависит явно от х, то есть
не зависит явно от х, то есть  . Уравнение Эйлера принимает вид
. Уравнение Эйлера принимает вид  , и, следовательно,
, и, следовательно, 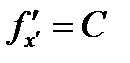 . Это уравнение называется первым интегралом уравнения Эйлера.
. Это уравнение называется первым интегралом уравнения Эйлера.
b. Функция 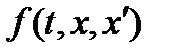 не зависит явно от t и х, то есть
не зависит явно от t и х, то есть  . Уравнение Эйлера записывается в виде
. Уравнение Эйлера записывается в виде  . Его общее решение имеет вид
. Его общее решение имеет вид  , а условие
, а условие 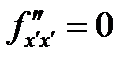 дает ОДУ первого порядка.
дает ОДУ первого порядка.
c. Функция 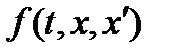 не зависит явно от t и
не зависит явно от t и  , то есть
, то есть 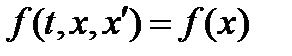 , или не зависит явно от
, или не зависит явно от  , то есть
, то есть  . Задача поиска экстремума в общем случае решения не имеет, т. к. уравнение Эйлера принимает вид
. Задача поиска экстремума в общем случае решения не имеет, т. к. уравнение Эйлера принимает вид  и не является дифференциальным, т. е. не содержит произвольных постоянных интегрирования и, вообще говоря, поэтому не удовлетворяет граничным условиям. Однако, если в частном случае решение уравнения
и не является дифференциальным, т. е. не содержит произвольных постоянных интегрирования и, вообще говоря, поэтому не удовлетворяет граничным условиям. Однако, если в частном случае решение уравнения  проходит через граничные точки х0, х1, то экстремаль существует.
проходит через граничные точки х0, х1, то экстремаль существует.
d. Подынтегральная функция имеет вид 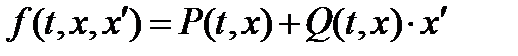 . Уравнение Эйлера в этом случае записывается в форме
. Уравнение Эйлера в этом случае записывается в форме
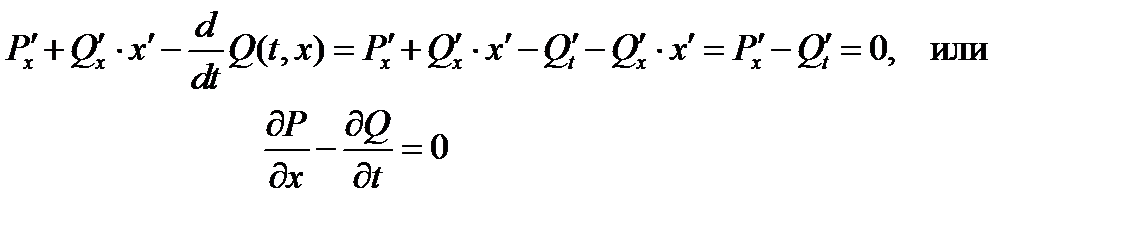
Это уравнение не является дифференциальным. Если его решение удовлетворяет граничным условиям, то экстремаль существует. Если  , то решения нет.
, то решения нет.
e. Функция 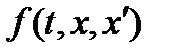 не зависит явно от t, то есть
не зависит явно от t, то есть 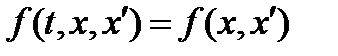 . Уравнение Эйлера в этом случае имеет вид:
. Уравнение Эйлера в этом случае имеет вид:
f. 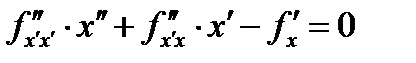 .
.
Если это уравнение умножить на  , то его можно преобразовать к виду
, то его можно преобразовать к виду
g. 
Полученное ДУ имеет первый интеграл  .
.
2. 5. 3. Алгоритм применения необходимых условий экстремума в зачах с фиксированными границами.
1. Найти 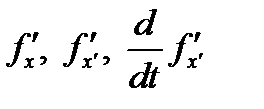 и записать уравнение Эйлера
и записать уравнение Эйлера 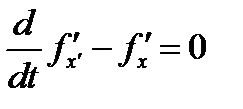 . Если функция соответствует одному из простейших случаев интегрируемости, можно использовать уравнения, полученные в пунктах 2. 5. 2 a - 2. 5. 2 e.
. Если функция соответствует одному из простейших случаев интегрируемости, можно использовать уравнения, полученные в пунктах 2. 5. 2 a - 2. 5. 2 e.
|
|
|
2. Найти общее решение уравнения Эйлера 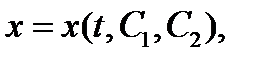 где С1 и С2 – произвольные постоянные.
где С1 и С2 – произвольные постоянные.
3. Определить постоянные С1 и С2 из граничных условий:
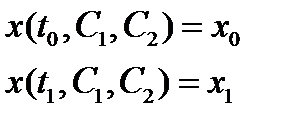
Пример. Найти экстремаль функционала
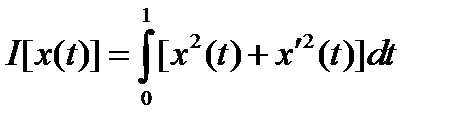 ,
,
удовлетворяющую граничным условиям х(0) = 0, х(1) =1.
Решаем задачу по алгоритму (п. 2. 5. 3. ).
1. Найдем 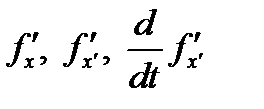 :
: 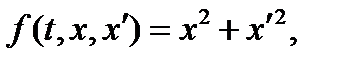 следовательно,
следовательно, 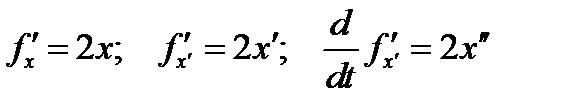 .
.
Уравнение Эйлера 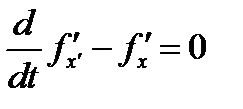 для данной задачи имеет вид
для данной задачи имеет вид  , или, после сокращения на 2,
, или, после сокращения на 2,  .
.
2. Решение линейного ОДУ второго порядка ищем в виде  . В результате подстановки
. В результате подстановки 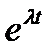 в дифференциальное уравнение
в дифференциальное уравнение  получаем характеристическое уравнение
получаем характеристическое уравнение
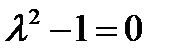 .
.
Корни характеристического уравнения 
Общее решение однородного уравнения
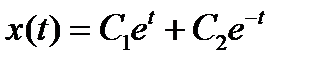 .
.
3. Определяем постоянные С1 и С2 из граничных условий

Получили систему двух уравнений с двумя неизвестными. Из первого уравнения следует  . Поставляя полученное соотношение во второе уравнение, получаем
. Поставляя полученное соотношение во второе уравнение, получаем  , откуда следует
, откуда следует 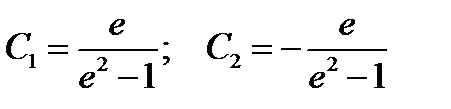 .
.
Уравнение экстремали  .
.
|
|
|


