Теоретико-множественный подход к определению произведения и частного для целых неотрицательных чисел. Законы умножения и деления. Деление с остатком.
Произведением целых неотрицательных чисел а и в называется такое целое неотрицательное число которое удовлетворяет следующим условиям: 1) а*Ь = а + а +...+а при в> I; 2) а * 1= а при в= 1; 3) а *0 = 0 при в = 0.
Теоретико-множественный смысл этого определения следующий. Если множества А 1, А2 ....Ав имеют по а элементов каждое и никакие два из них не пересекаются, то их объединение содержи т а*Ь элементов. Следовательно, произведение а*Ь —это число элементов в объединении в попарно непересекающихся множеств, каждое из которых содержит по а элементов. Равенств а а - 1 = а и а-0 = 0 принимаются по условию. Действие, при помощи которого находят произведение чисел а и в, назв умножением; числа, которые умнож, наз множителями. Произведение любых целых неотрицательных чисел существ, и оно единственно. Док т.к произвед целых неотр чисел опред ч/з сумму одинак слагаем котор находит как число эл-тов и это объединен наход единств образом знач и сумма всегд сущест и нах единств образ. С теоретико-множественной точки зрения произведение a  b целых неотрицательных чисел есть число элементов в декартовом произведении множеств А и В, таких, что n(A) = a, n(B) = b. A*b = n(A) * n(B) = n(А хВ). Рассмотрим коммутативность с точки зрения теоретико-множественного подхода, т.е. ab =ba. Пусть n(A)= a, n(B) = b. Тогда по определению произведения ab = n((А хВ). Но множества АхВ = ВхА равномощны: каждой паре (а;b) из множества АхВ можно поставить в соответствие единственную пару (b;a) из множества ВхА, и наоборот. Следовательно, n(АхВ) = n(ВхА). Значит ab = ba. Ассоциативность (a*b)*c = a*(b*c) вытекает из того, что множества ((АхВ)хС)=Ах(ВхС) равномощны, а значит n((АхВ)хС)=n(Ах(ВхС)). Дистрибутивность рассматривают относительно сложения и вычитания. Рассмотрим относительно сложения: (a + b)*c = a*c + bc. По определению произведения имеем (a+b)c=n((АUВ)хС). Но (AUB)xC=(AxC)U(BxC), поэтому n(AUB)xC=n(AxC)U(BxC), а значит и (a + b)c = ac + bc.
b целых неотрицательных чисел есть число элементов в декартовом произведении множеств А и В, таких, что n(A) = a, n(B) = b. A*b = n(A) * n(B) = n(А хВ). Рассмотрим коммутативность с точки зрения теоретико-множественного подхода, т.е. ab =ba. Пусть n(A)= a, n(B) = b. Тогда по определению произведения ab = n((А хВ). Но множества АхВ = ВхА равномощны: каждой паре (а;b) из множества АхВ можно поставить в соответствие единственную пару (b;a) из множества ВхА, и наоборот. Следовательно, n(АхВ) = n(ВхА). Значит ab = ba. Ассоциативность (a*b)*c = a*(b*c) вытекает из того, что множества ((АхВ)хС)=Ах(ВхС) равномощны, а значит n((АхВ)хС)=n(Ах(ВхС)). Дистрибутивность рассматривают относительно сложения и вычитания. Рассмотрим относительно сложения: (a + b)*c = a*c + bc. По определению произведения имеем (a+b)c=n((АUВ)хС). Но (AUB)xC=(AxC)U(BxC), поэтому n(AUB)xC=n(AxC)U(BxC), а значит и (a + b)c = ac + bc.
Если а – число элементов множества А и множество А разбито на b попарно непересекающихся подмножеств, то частным чисел а и b называется число элементов каждого подмножества разбиения. Если а – число элементов множества А и множество А разбито на попарно непересекающиеся подмножества, в каждом из которых b элементов, то частным чисел а и b называется число подмножеств разбиения. Действие, при помощи которого находят частное, называется делением, число а – делимым, число b – делителем. Свойства: Правило деления суммы на число. Если числа а и b делятся на число с, то и их сумма а + b делится на с. Частное, получаемое при делении суммы а + b на число с, равно сумме частных получаемых при делении а на с и b на с, т.е. (а + b): с = а: с + b: с. Данное правило можно истолковать с точки зрения теоретико-множественного подхода. Если частные а: с и b: с существуют, то (а + b): с= а: с + b: с. Пусть n(A) = a, n(B) = b,причем А 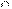 В =∅. Если множества А и В разбить на равночисленные подмножества, состоящие из с элементов, то и объединение этих множеств допускает такое разбиение. Если при этом множество А состоит из а: с подмножеств, а множество В состоит из b: с подмножеств, то АUВ состоит из а: с + b: с. это значит, что (а + b): с = а: с + b: с. Правило деления числа на произведение. Если натуральное число а делится на натуральные числа b и с, то чтобы разделить а на произведение чисел b и с, достаточно разделить число а на b(c) и полученное частное разделить на с(b): а: (b* c) = (a: b): c = (a: c): b. Правило умножения числа на частное двух чисел. Чтобы умножить число на частное двух чисел, достаточно умножить это число на делимое и полученное произведение разделить на делитель, т.е. a (b: c) = (a b): c. Правило деления произведения на число. Чтобы разделить произведение нескольких целых неотрицательных чисел на натуральное число, достаточно один из множителей разделить на это число и полученное частное умножить на оставшиеся множители, т.е., если а: n, то (a*b*c): n = (a: n)* b*c. Разделить натуральное число а на натуральное число b с остатком – это значит найти такие натуральные целые числа q и r, что а = bq + r, где 0
В =∅. Если множества А и В разбить на равночисленные подмножества, состоящие из с элементов, то и объединение этих множеств допускает такое разбиение. Если при этом множество А состоит из а: с подмножеств, а множество В состоит из b: с подмножеств, то АUВ состоит из а: с + b: с. это значит, что (а + b): с = а: с + b: с. Правило деления числа на произведение. Если натуральное число а делится на натуральные числа b и с, то чтобы разделить а на произведение чисел b и с, достаточно разделить число а на b(c) и полученное частное разделить на с(b): а: (b* c) = (a: b): c = (a: c): b. Правило умножения числа на частное двух чисел. Чтобы умножить число на частное двух чисел, достаточно умножить это число на делимое и полученное произведение разделить на делитель, т.е. a (b: c) = (a b): c. Правило деления произведения на число. Чтобы разделить произведение нескольких целых неотрицательных чисел на натуральное число, достаточно один из множителей разделить на это число и полученное частное умножить на оставшиеся множители, т.е., если а: n, то (a*b*c): n = (a: n)* b*c. Разделить натуральное число а на натуральное число b с остатком – это значит найти такие натуральные целые числа q и r, что а = bq + r, где 0  r < b. Пусть а = n(A) и множество А разбито на множества A1, A2, …, Aq, R, так, что множества A1, A2, …, Aq равномощны, а множество R содержит меньше элементов, чем каждое из множеств A1, A2, …, Aq. Тогда, если n(A1), n(A2), …,n(Aq) = b, а n(R) = r, то a = bq + r, где 0
r < b. Пусть а = n(A) и множество А разбито на множества A1, A2, …, Aq, R, так, что множества A1, A2, …, Aq равномощны, а множество R содержит меньше элементов, чем каждое из множеств A1, A2, …, Aq. Тогда, если n(A1), n(A2), …,n(Aq) = b, а n(R) = r, то a = bq + r, где 0  r < b. Причем число q равномощных множеств является неполным частным при делении а на b, а число элементов в R – остатком при этом делении.
r < b. Причем число q равномощных множеств является неполным частным при делении а на b, а число элементов в R – остатком при этом делении.
Воспользуйтесь поиском по сайту:


 b целых неотрицательных чисел есть число элементов в декартовом произведении множеств А и В, таких, что n(A) = a, n(B) = b. A*b = n(A) * n(B) = n(А хВ). Рассмотрим коммутативность с точки зрения теоретико-множественного подхода, т.е. ab =ba. Пусть n(A)= a, n(B) = b. Тогда по определению произведения ab = n((А хВ). Но множества АхВ = ВхА равномощны: каждой паре (а;b) из множества АхВ можно поставить в соответствие единственную пару (b;a) из множества ВхА, и наоборот. Следовательно, n(АхВ) = n(ВхА). Значит ab = ba. Ассоциативность (a*b)*c = a*(b*c) вытекает из того, что множества ((АхВ)хС)=Ах(ВхС) равномощны, а значит n((АхВ)хС)=n(Ах(ВхС)). Дистрибутивность рассматривают относительно сложения и вычитания. Рассмотрим относительно сложения: (a + b)*c = a*c + bc. По определению произведения имеем (a+b)c=n((АUВ)хС). Но (AUB)xC=(AxC)U(BxC), поэтому n(AUB)xC=n(AxC)U(BxC), а значит и (a + b)c = ac + bc.
b целых неотрицательных чисел есть число элементов в декартовом произведении множеств А и В, таких, что n(A) = a, n(B) = b. A*b = n(A) * n(B) = n(А хВ). Рассмотрим коммутативность с точки зрения теоретико-множественного подхода, т.е. ab =ba. Пусть n(A)= a, n(B) = b. Тогда по определению произведения ab = n((А хВ). Но множества АхВ = ВхА равномощны: каждой паре (а;b) из множества АхВ можно поставить в соответствие единственную пару (b;a) из множества ВхА, и наоборот. Следовательно, n(АхВ) = n(ВхА). Значит ab = ba. Ассоциативность (a*b)*c = a*(b*c) вытекает из того, что множества ((АхВ)хС)=Ах(ВхС) равномощны, а значит n((АхВ)хС)=n(Ах(ВхС)). Дистрибутивность рассматривают относительно сложения и вычитания. Рассмотрим относительно сложения: (a + b)*c = a*c + bc. По определению произведения имеем (a+b)c=n((АUВ)хС). Но (AUB)xC=(AxC)U(BxC), поэтому n(AUB)xC=n(AxC)U(BxC), а значит и (a + b)c = ac + bc.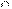 В =∅. Если множества А и В разбить на равночисленные подмножества, состоящие из с элементов, то и объединение этих множеств допускает такое разбиение. Если при этом множество А состоит из а: с подмножеств, а множество В состоит из b: с подмножеств, то АUВ состоит из а: с + b: с. это значит, что (а + b): с = а: с + b: с. Правило деления числа на произведение. Если натуральное число а делится на натуральные числа b и с, то чтобы разделить а на произведение чисел b и с, достаточно разделить число а на b(c) и полученное частное разделить на с(b): а: (b* c) = (a: b): c = (a: c): b. Правило умножения числа на частное двух чисел. Чтобы умножить число на частное двух чисел, достаточно умножить это число на делимое и полученное произведение разделить на делитель, т.е. a (b: c) = (a b): c. Правило деления произведения на число. Чтобы разделить произведение нескольких целых неотрицательных чисел на натуральное число, достаточно один из множителей разделить на это число и полученное частное умножить на оставшиеся множители, т.е., если а: n, то (a*b*c): n = (a: n)* b*c. Разделить натуральное число а на натуральное число b с остатком – это значит найти такие натуральные целые числа q и r, что а = bq + r, где 0
В =∅. Если множества А и В разбить на равночисленные подмножества, состоящие из с элементов, то и объединение этих множеств допускает такое разбиение. Если при этом множество А состоит из а: с подмножеств, а множество В состоит из b: с подмножеств, то АUВ состоит из а: с + b: с. это значит, что (а + b): с = а: с + b: с. Правило деления числа на произведение. Если натуральное число а делится на натуральные числа b и с, то чтобы разделить а на произведение чисел b и с, достаточно разделить число а на b(c) и полученное частное разделить на с(b): а: (b* c) = (a: b): c = (a: c): b. Правило умножения числа на частное двух чисел. Чтобы умножить число на частное двух чисел, достаточно умножить это число на делимое и полученное произведение разделить на делитель, т.е. a (b: c) = (a b): c. Правило деления произведения на число. Чтобы разделить произведение нескольких целых неотрицательных чисел на натуральное число, достаточно один из множителей разделить на это число и полученное частное умножить на оставшиеся множители, т.е., если а: n, то (a*b*c): n = (a: n)* b*c. Разделить натуральное число а на натуральное число b с остатком – это значит найти такие натуральные целые числа q и r, что а = bq + r, где 0  r < b. Пусть а = n(A) и множество А разбито на множества A1, A2, …, Aq, R, так, что множества A1, A2, …, Aq равномощны, а множество R содержит меньше элементов, чем каждое из множеств A1, A2, …, Aq. Тогда, если n(A1), n(A2), …,n(Aq) = b, а n(R) = r, то a = bq + r, где 0
r < b. Пусть а = n(A) и множество А разбито на множества A1, A2, …, Aq, R, так, что множества A1, A2, …, Aq равномощны, а множество R содержит меньше элементов, чем каждое из множеств A1, A2, …, Aq. Тогда, если n(A1), n(A2), …,n(Aq) = b, а n(R) = r, то a = bq + r, где 0  r < b. Причем число q равномощных множеств является неполным частным при делении а на b, а число элементов в R – остатком при этом делении.
r < b. Причем число q равномощных множеств является неполным частным при делении а на b, а число элементов в R – остатком при этом делении.

