 |
Числовая функция. Способы задания. Уравнение линии. График функции. Линейная и квадратичная функции, их свойства и графики.
|
|
|
|
Числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множества вещественных чисел R или множества комплексных чисел С.
Способы задания функции:
Словесный - с помощью естественного языка (у равно целая часть от х)
Аналитический - с помощью формулы и стандартных обозначений (f = x!)
Графический - с помощью графика
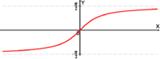
Фрагмент графика функции
у = arctg x
Табличный - c помощью таблицы значений
х 0 1 2 3 4 5 6 7 8 9
у 1 1 2 3 5 8 13 21 34 55
Аналитический способ. Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно, кусочное задание, то есть различное для различных значений аргумента.
Примеры:
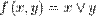
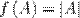
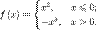
Табличный способ. Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:
х у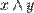 
0 0 0
0 1 0
1 0 0
1 1 1
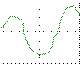
Графический способ. Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.
Рекурсивный способ. Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.
|
|
|
Примеры: факториал; числа Фибоначчи; функция Аккермана.
Словесный способ. Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные.
Примеры:
функция, возвращающая цифру в записи числа пи по её номеру;
функция, возвращающая число атомов во вселенной в определённый момент времени;
функция, принимающая в качестве аргумента человека, и возвращающая число людей, которое родится на свет после его рождения.
Линией на плоскости назовём геометрическое место точек на плоскости, координаты которого удовлетворяют некоторому условию. Функция, которая каждому числу по некоторому правилу ставит в соответствие пару чисел, называется уравнением линии.
График функции — множество точек, у которых абсциссы являются допустимыми значениями аргумента х, а ординаты — соответствующими значениями функции у.
Линейная функция — функция вида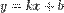 
(для функций одной переменной).
Основное свойство линейных функций: приращение функции пропорционально приращению аргумента. То есть функция является обобщением прямой пропорциональности.
График линейной функции является прямой линией.
Свойства:
k является тангенсом угла, который образует прямая с положительным направлением оси абсцисс.
При k > 0, прямая образует острый угол с осью абсцисс.
При k < 0, прямая образует тупой угол с осью абсцисс.
При k = 0, прямая параллельна оси абсцисс.
b является показателем ординаты точки пересечения прямой с осью ординат.
При b = 0, прямая проходит через начало координат.
|
|
|
Квадратичная функция — функция, которую можно задать формулой вида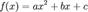 
, где 
.
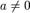График квадратичной функции называется параболой.
В общем виде уравнение квадратичной функции записывается так: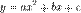 
. Координаты вершины параболы: 
.
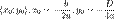Прямая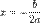 
является осью симметрии графика квадратичной функции.
При а < 0 ветви параболы направлены вниз, при а > 0 — вверх.
Свойства квадратичной функции y=x2:
1) Областью определения функции у = х 2 является множество всех действительных чисел, т.е.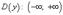 
.
2) Множеством значений функции является промежуток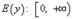 
.
3) Значение функции y=0 является наименьшим, а наибольшего значения функция не имеет.
4) Функция у = х 2 является четной, график симметричен относительно оси Оу.
5) Функция непериодическая.
6)Парабола у = х 2 имеет с осями координат единственную общую точку (0;0) - начало координат.
7) Значение аргумента x=0 является нулем функции.
8) На промежутке 
функция убывающая, а на промежутке 
- возрастающая.
9) Функция принимает положительные значения на множестве 
, т.е. все точки параболы, кроме начала координат.
|
|
|
