 |
Прямая и обратная пропорциональности, их графики и свойства. Цена, количество и стоимость товара, зависимости между ними.
|
|
|
|
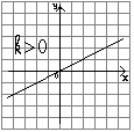
Числовая функция – такое соответствие между числовым множеством Х и множеством R действ. чисел, при котором каждому числу из множества Х сопоставляется единственное число из множества R. Прямая пропорц. - функция вида: y = kx; где k ϵ R. График – прямая, проходящая через начало координат. Св-ва: 1)D(f): R; 2) E(f): (- ∞; ∞); 3)Корни: (0;0); 4) Промеж знаков пост: k > 0: y > 0 – (0; ∞), y < 0 – (- ∞; 0); k < 0: y > 0 – (- ∞; 0), y < 0 – (0; ∞); 5) Экстремумы: нет; 6)Монотонность: ↑ - k > 0,↓ - k < 0; 7) Наиб, наим – нет; 8)Не четная; 9) Непериодическая; 10)Непрерывна.
График - прямая, строим по двум точкам.

Обратная пропорц. -функция вида:y = k/x; где k ϵ R. График – гипербола. Св-ва: 1)D(f): (- ∞;0) ν (0; ∞); 2)E(f): (- ∞;0) ν (0; ∞); 3)Корней нет;4)Промеж знаков пост: k > 0: y > 0 – (0; ∞), y < 0 – (- ∞; 0); k < 0: y > 0 – (- ∞; 0), y < 0 – (0; ∞); 5)Экстремумы: нет; 6)Монотонность: ↑ при k < 0,↓ при k > 0; 7)Наиб, наим – нет; 8)Не четная; 9) Непериодическая; 10)Прерывается в точке (0;0).
График - гипербола, строим заполняя таблицу.


Цена – это величина, которая показывает, сколько стоит один предмет (один килограмм продукта, одна коробка чая и т.д.). Количество - это число, которое показывает, сколько предметов мы купили. Стоимость - это величина, которая показывает, сколько будут стоить все те предметы, которые мы купили. Все эти три величины связаны между собой. Если у нас имеются любые две из них, то мы можем найти и третью неизвестную величину. Формула стоимости: С = К * Ц.Из этой формулы можно вывести формулы для других входящих в неё величин. 1) Ц = С / К. 2) К = С / Ц.
| Цена | Стоим | Кол-во |
| const | ↑ | ↑ |
| ↑ | const | ↓ |
| ↑ | ↑ | const |
36. Величина. Свойства скалярных величин (на примере массы тела). Измерение величин. Основные и производные величины.
|
|
|
Длина, площадь, масса, скорость, стоимость — величины. Первоначальное знакомство с ними происходит в начальной школе, где величина наряду с числом является ведущим понятием. Величины — это особые свойства реальных объектов или явлений. Например, свойство предметов иметь протяженность называется длиной. Однородные величины выражают одно и то же свойство объектов некоторого множества и могут быть выражены в одних единицах измерения (н-р, глубина, высота, ширина и т.д. – протяженность в пространстве). Разнородные величины выражают различные свойства объектов. Так, длина и площадь — это разнородные величины.
В математике выделяют скалярные, векторные и тензорные величины. Скалярные величины определяются только численными значениями (н-р, длина, площадь, масса и т.д.)Векторные величины определяются численным значением и направлением (н-р: вес, сила, скорость, ускорение…). Тензорные величины задаются 4-мя и более характеристиками
Величины обладают рядом свойств:
1. Любые две величины одного рода сравнимы: они либо равны, либо одна меньше другой. Иными словами, для величин одного рода имеют место отношения «равно», «меньше» и «больше» и для любых величин а и b справедливо одно и только одно из отношений: а < Ь, а = Ь, а > Ь. Например, масса яблока меньше массы арбуза.
2. Величины одного рода можно складывать, в результате сложения получится величина того же рода. Другими словами, для любых двух величин а и b однозначно определяется величина а + Ь, ее называют суммой величин а и Ь.
Например, к 3 тоннам зерна добавили еще 5 тонн, получили 8 тонн зерна. 3т + 5т = 8т
3. Величину умножают на действительное число, получая в результате величину того же рода. Если умножить величины друг на друга получится величина другого рода.
Например, 6кг * 3 = 18 кг
4. Величины одного рода вычитают, определяя разность величин через сумму: разностью величин а и b называется такая величина с, что а = Ь + с.
|
|
|
Например, 12кг – 7кг = 5кг, 12 = 7 + 5
5. Величины одного рода можно делить друг на друга, получится число, показывающее во сколько раз одна величина больше другой. Величину можно делить на действительное число, получится величина того же рода.
Например: 36 кг: 4 кг = 9 (раз), 56 кг: 8 = 7 (кг)
Измерение заключается в сравнении данной величины с некоторой величиной того же рода, принятой за единицу. Процесс сравнения зависит от рода рассматриваемых величин: для длин он один, для площадей — другой,
для масс — третий и т. д. Но каким бы ни был этот процесс, в результате измерения величина получает определенное численное значение при выбранной единице.
Если дана величина а и выбрана единица величины е, то в результате измерении величины а находят такое действительное число х, что а =х - е. Эти число х называют численным значением величины а при единице величины е.
Согласно определению любую величину можно представить в виде произведения некоторого числа и единицы этой величины. Например, 7 кг = 7* 1 кг, 12 см=12*1 см, 3 ч = 3*1 ч.
Международная система единиц (СИ) — это единая универсальная практическая система единиц для всех отраслей науки, техники, народного хозяйства и преподавания. В этой системе семь основных единиц (метр, килограмм, секунда, ампер, кельвин, моль и кандела) и две дополнительные единицы (радиан и стерадиан).
Для массы кратной единицей является мегаграмм (M r), а дольными — грамм (г), миллиграмм (мг), микрограмм (м кг).
|
|
|


