 |
GERT (graphical evaluation and review technique)
|
|
|
|
· GERT – это стохастическая сеть
· По аналогии с PERT длительность работ является случайной величиной
· В GERT не учитываются ограничения на ресурсы (напомню, что в CPM ограничения на ресурсы отсутствуют, в PERT ограничения не ресурсы не учитываются)
· В GERT допускаются контуры и петли
В GERT событие разделено на две части. Одна часть отвечает за входящие события, другая часть отвечает за исходящие события.
Опыт показывает, что более эффективным является введение в сеть всеж вероятных альтернатив работ до начала реализации проекта, чем корректировка сетив процессе реализации.
Схема применения:
1. Описание проекта стохастической сетью
2. Сбор числовых данных, характеризующих каждую дугу сети
3. Минимизация построенной сети
4. Преобразование замещающей сети (функции) к форме, позволяющей определить длительности и вероятности реализации проекта, а также расчет длительностей и вероятностей.
5. Анализ и оценка результатов упрощенной сети
В сети существует 2 типа событий: детерминированные (в виде окружности) и вероятностные (в виде «капли»). Дуги, выходящие из детерминированных событий имеют вероятность реализации р=1 (должны быть выполнены, чтобы проект был реализованным), но из всех ветвей, выходящих из вероятностного события только одна будет достаточной для доведения проекта до логического завершения.
Входы:
· Вершины типа «И» - для событий, которые наступают, когда все предшествующие им работы окажутся выполненными
· Вершины типа «ИЛИ» - для событий, которые наступают, когда хотя бы одна их предшествующих им работ окажется выполнена.
· Вершина типа «исключающее ИЛИ» - для событий, которые наступают, когда будет выполнена ровно одна из предшествующих работ. Событию предшествуют взаимоисключающие события.
|
|
|
Выходы:
· «И» - детерминированный выход, связанный с событиями, наступление которых означает выполнение всех следующих за такими событиями работ. (если событие наступает, то запускаются все работы которые из него выходят(данное событие наступает только тогда, когда все входящие работы выполняются)).
· «ИЛИ» - вероятностный выход, связанный с событиями, наступление которых ведет за собой выполнение, как минимум, одной из следующих за ним работ. Сумма их вероятностей на выходе должна быть равна 1.
Описание стороны выхода может иметь характер решающей функции. После наступления события в соответствии с это функцией определяется судьба следующих за ним работ. Сумма вероятностей, соответствующих каждой ветви, выходящей из вероятностного события должна быть равна 1.
Альтернативные работы: это работа, кот. выходит из события и обратно в него входит, например НИОКР: если нуждаемся в доработке, то повторяем опытно-конструкторские работы и соответственно возвращаемся возвращаемся на начало события. р1,р2,р3 - вероятности того что работы будут выполняться. (только 1 из них будет выполняться на выходе из события).
CAAN: Combinatorial and Algorithmic Aspects of Networking.
Автор: Дмитрий Голенко-Гинзбург (1973)
- это гибрид DCPM и GERT. задача здесь сложно решается, т.к. идет перебор всех вариантов (алгоритм CAAN). данная модель является промежуточной.
- Сетевой граф AoA с одним начальным событием и минимум 2-мя конечными
- Основан на GERT и также включает в себя вершины:
- Детерминированные
-
Событие наступает когда только предыдущие работы выполнены -
Наступает, когда только 1 из работ выполнена
- Стохастические
-
Инициирует запуск 1 из работ с некоторой вероятностью -
Наступает тогда и только тогда, когда 1 из работ завершена и инициирует только 1 работу
- Работы, выходящие из стохастических вершин, могут выбираться случайно (стохастические работы) или человеком (альтернативные работы)
|
|
|
- Из одной вершины могут выходить работы только одного типа: либо детерминированные, либо стохастические, либо альтернативные
В модели CAAN целевой функцией является время выполнения проекта, а ограничением – его стоимость, либо наоборот. Принятие решений сводится к выбору направления хода работ по проекту в каждой из последовательно достигаемых вершин типа «И – ИЛИ», поскольку вершины a носят неконтролируемый характер.
Таким образом, оптимальная задача решается на следующих этапах:
1. Построение графа исходов
2. Выделить из дерева исходов все совокупные варианты и допустимые планы. Процесс начинается при t = 0, то есть до начала реализации проекта.
§ Формирование графа, содержащего только
§ стохастические вершины (α-frame)
§ Определение макс.путей в новом графе
§ Определение допустимого плана
3. Определить для каждого из совокупных вариантов значения целевой функции и ограничений (обычно в виде математических ожиданий).
4. Определить оптимальный совокупный вариант и управлять проектом по оптимальной траектории (то есть, по оптимальному направлению) до следующей ветвящейся вершины детерминированного типа. В этой вершине вновь решить оптимальную задачу для усеченной (обновленной) модели дерева исходов, начиная с этапа 1. Процесс управления повторяется до окончания реализации проекта.
Пример:
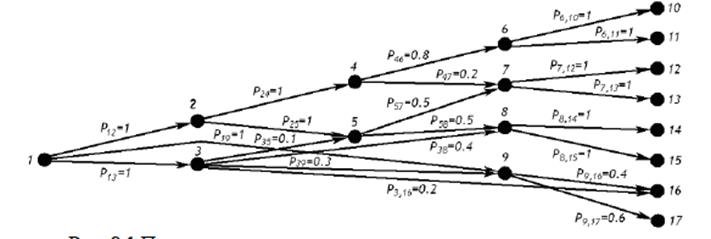Предполагается редуцировать расчеты CAAN к модели GERT. В основном это делается перебором.
Применение:
o Министерство авиации для планирования R&D проектов, система автоматизации – КОМПАС
o Центральный ленинградский оптический институт
o Проектирование химических заводов в Израиле
|
|
|
