Функция принадлежности трапециевидного нечеткого числа

Поскольку границы интервала заданы нечетко, то разумно ввести абсциссы вершин трапеции следующим образом:

а = (а₁+а₂)/2, в = (в₁+в₂)/2, (2.5)

при этом отстояние вершин а₁, а₂ и в₁, в₂ соответственно друг от друга обуславливается тем, что какую семантику мы вкладываем в понатие «примерно»: чем больше разброс квазистатистики, тем боковые ребра трапеции являются более пологими. В предельном случае понятие «примерно» выраждается в понятие «где угодно».

Если мы оцениваем параметр качественно, например, высказавшись «Это значение параметра является средним», необходимо ввести уточняющее высказывание типа «Среднее значение – это примерно от a до b», которое есть предмет экспертной оценки (нечеткой классификации), и тогда можно использовать для моделирования нечетких классификаций трапезоидные числа. На самом деле, это самый естественной способ неуверенной классификации.

Треугольные нечеткие числа

Теперь для той же лингвистической переменной зададим терм-множество Т₁={U приблизительно равно а}. Ясно, что а ± d» а, причем по мере убывания d до нуля степень уверенности в оценке растет до единицы. Это, с точки зрения функции принадлежности, придает последней треугольный вид (рис. 2.4), причем степень приближения характеризуется экспертом.

Функция принадлежности треугольного нечеткого числа

Треугольные числа – это самый часто используемый на практике тип нечетких чисел, причем чаще всего - в качестве прогнозных значений параметра.

Операции над нечеткими числами

Целый раздел теории нечетких множеств – мягкие вычисления (нечеткая арифметика) - вводит набор операций над нечеткими числами. Эти операции вводятся через операции над функциями принадлежности на основе так называемого сегментного принципа.

Определим уровень принадлежности a как ординату функции принадлежности нечеткого числа. Тогда пересечение функции принадлежности с нечетким числом дает пару значений, которые принято называть границами интервала достоверности.

 

Зададимся фиксированным уровнем принадлежности a и определим соответствующие ему интервалы достоверности по двум нечетким числам и : [a₁, a₂] и [b₁, b₂], соответственно. Тогда основные операции с нечеткими числами сводятся к операциям с их интервалами достоверности. А операции с интервалами, в свою очередь, выражаются через операции с действительными числами - границами интервалов:

· операция "сложения":

[a₁, a₂] (+) [b₁, b₂] = [a₁ + b₁, a₂ + b₂], (2.6)

· операция "вычитания":

[a₁, a₂] (-) [b₁, b₂] = [a₁ - b₂, a₂ - b₁], (2.7)

· операция "умножения":

[a₁, a₂] (´) [b₁, b₂] = [a₁ ´ b₁, a₂ ´ b₂], (2.8)

· операция "деления":

[a₁, a₂] (/) [b₁, b₂] = [a₁ / b₂, a₂ / b₁], (2.9)

· операция "возведения в степень":

[a₁, a₂] (^) i = [a₁ⁱ, a₂ⁱ]. (2.10)

Из существа операций с трапезоидными числами можно сделать ряд важных утверждений (без доказательства):

· действительное число есть частный случай треугольного нечеткого числа;

· сумма треугольных чисел есть треугольное число;

· треугольное (трапезоидное) число, умноженное на действительное число, есть треугольное (трапезоидное) число;

· сумма трапезоидных чисел есть трапезоидное число;

· сумма треугольного и трапезоидного чисел есть трапезоидное число.

Проблема вычисления поздних сроков

Проблема возникает из-за правил сложения интервальных чисел, мы получаем у 0 работы поздние сроки от -1 до 1, а в реальности должно быть от 0 до 0. Очень часто выдает невозможные значения.

 

Билет 18. Интервальные числа. Интервальный PERT.

Интервальные числа

Интервальным числом мы будем называть интервал значений

Введем операции сложения и вычитания интервальных чисел.

,

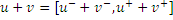
Пример:

Продолжительность работа u варьируется в интервале от 1 до 2 дней. Продолжительность работа v варьируется в интервале от 5 до 7 дней.

Тогда последовательность работ u->v будет выполняться не менее чем 6 дней и не более чем 9 дней. То есть, ее продолжительность является интервальным числом.

Пример:

К сожалению, этому результату нельзя дать такую понятную интерпретацию как в случае со сложением.

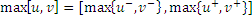
Интервальный PERT

Пример. Проект из одной работы продолжительностью от 0 до 1 дня.

[0, 1]

 

Ранний старт работы 0,1 – обычное неинтервальное число, 0 (просто потому, что проект начинается в нулевой день, модель с непрерывным временем). Может быть записано в интервальном виде как [0, 0].

Следовательно, ранний финиш

(сложили по правилам сложения интервальных чисел ранний старт с продолжительностью)

Поздний финиш равен раннему, т.к. нет даты навязанного финиша.

Если теперь найти поздний старт, вычтя из позднего финиша продолжительность, по правилам вычитания интервальных чисел, то получим

Это нонсенс, должно было получиться [0,0]. Это говорит нам о том, что должны быть какие-то другие методы поиска поздних стартов и резервов.

Конфигурацией будем называть фиксированное расписание, которое получается при выборе конкретных значений продолжительностей для всех работ, из интервала. При этом проект становится обычным, без интервальных чисел.

Можно построить пространство конфигураций – множество всех возможных конфигураций.

Для каждой работы kl проекта ранние и поздние сроки, а также резервы будут интервальными числами.

Как я понимаю, для позднего старта и раннего финиша аналогично

По определению

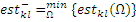
То есть, минимально возможное значение раннего старта данной работы из всех возможных конфигураций.

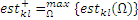
И так со всеми ранними и поздними сроками и резервами – там, где левая граница интервала, минимум, где правая – максимум.

Пример.

Можно видеть, что путь 1-3-5 ни в одной конфигурации не является критическим.

При , , , 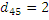путь 1-3-4-5 является критическим

 

Определение. Работа, которая в какой-либо конфигурации является критической, называется возможно критической.

Существуют достоверно (абсолютно) критические работы – критические во всех конфигурациях.

 

Если работа возможно критическая, то нижняя граница резерва равна нулю. Обратное тоже верно (если нулю равна нижняя граница резерва, то работа возможно критическая).

А если и верхняя, то достоверно критическая.

Между тем, из равенства ранних и поздних сроков (равны как верхние, так и нижние границы интервалов) не следует критичность работы ни в каком смысле.

 

Вычисление ранних и поздних сроков.

Для вычисления ранних используется обычное сложение интервальных чисел.

Для вычисления поздних сроков и резервов используются два алгоритма. Если мне не изменяет память, Царьков писал, что из знать не надо.

⇐ Предыдущая12345678910

Поделиться:

Воспользуйтесь поиском по сайту: