 |
Билет № 7. Понятие критической работы в стохастических моделях и индексы критичности
|
|
|
|
Критическая работа в СРМ – та, которая лежит на критическом пути (т.е. самом длинном), и резерв которой равен нулю.
НО! В моделях стохастических такое определение критич. работы не подходит, т.к. любой путь может стать критическим, а как следствие, теоретически любая работа может быть критической.
CI (criticality index) – индекс (0 до 1), отражающий отношение количества попадания работы на критический путь к общему числу симуляций (монте-карло).
o PCI (Path Criticality Index) – вероятность того, что путь является самым длинным в сети.
Пусть П={πh} – набор всех путей в сетевом графике, а L(πh) – случайная переменная, которая равна длительности пути πh. Тогда L(πh)=∑tϵ πhdi где di – случайная переменная, равная длительности работы i.
Тогда индекс критичности для пути πh будет равен
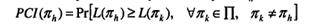
· Activity criticality index (ACI) = вероятность, что конкретная работа попадет на критический путь
Для вычисления АСI, нужно (3 шага):
- Рассчитать PCI для всех путей
- Найти пути, содержащие данную работу
- Посчитать ACI путем сложения значений PCI всех путей, куда она входит.
Однако, 3ий шаг сложен в расчетах ввиду взаимосвязей путей, пересечений и проч. Поэтому умы современности придумали несколько методов:
o Аналитические подходы (использовать приблизительные оценки;
o использовать вероятностн.модели для нахождения «более приоритетного критического пути» и пр.), или использовать Монте-Карло.
Но некто Willams не был доволен индексом ACI по ряду причин:
- проджектменеджерам информация идекса ACI не очень понятна, т.к. они не мыслят в терминах «вероятностей»,
- индекс не может быть использован в условиях ограничений на ресурсы
- может давать результаты, которые противоположны интуитивным оценкам менеджеров (странный минус, ну да ладно).
|
|
|
Свои замечания он проиллюстрировал
Ниже – 2 независимые работы.

Получается, что работа 1 – ОЧЕНЬ критичная (ACI 1 = 99%). И если мы начнем корректировать длительность работы 1, то она (как всем ясно) станет более критичной, но от этого значение ACI не изменяется, а должно => ACI не годится, по мнению Willams, и он предложил индексы критичности.
Индекс критичности работы (SI, Significance index):
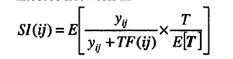
TF(ij) = tj(L) – ti(Е) – yij, yij – длительность реализации работы ij, TF – полный (свободный?) резерв? T – время завершения проекта, E[T] – ожидаемое время завершения проекта. Tj(E), Tj(L) – раннее возможное и позднее разрешенное время выполнения работы – события j.
Для приведенного примера выше, получаются след.результаты:
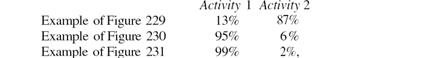
Но! Не тут-то было. Некто Elmaglharby раскритиковал индекс SI (т.к. опять получаются равные значения индекса для работ, очевидно разных по значимости для проекта (ex: 1 работа длительностью 100, 2я работа – 10 (вер-ть 0,5) или 20 (вер-ть 0,5), а SI1=SI2=1), и Willams решил доработать свой индекс, поэтому мы можем наслаждаться ещё одним:
Индекс критичности (CRI – Critically Index), который равен абсолютному значению корреляции между длительностью работы di и полной длительностью проекта T.
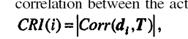
Где для 2 случ.пересенных корреляция и ковариация соответственно равны:

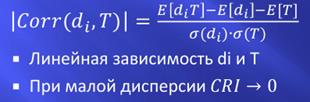
У CRI 2 больших плюса:
1. возможность использовать при наличии ограничений на ресурсы
2. может использоваться не только для длительности работ, но и для др.неопределенных аспектов проекта. В качестве примера – stochastic branches in generalized activity networks – понятия не имею, что это.
Однако не всё так хорошо. Упомянутый выше Elmaglharby нашел и в CRI ряд недостатков:
- Он измеряет только линейную зависимость м\д продолжительностью проекта и работы, но эта зависимость может быть и нелинейной
- Требует больших вычислительных возможностей, т.к. много работ и, соотв-но, много взаимосвязей
- что-то связанное с тем, что если продолжительность работы имеет малую вариацию, то CRI для нее близок к 0, даже если она на критическом пути.
|
|
|
|
|
|


