 |
Билет № 13. Применение математического программирования для решения задачи RCPSP
|
|
|
|
Введение
Задачи, относящиеся к типу RCPSP (resources constraint project scheduling problem), представляют собой задачи по минимизации времени продолжительности проекта с ограничением на ресурсы. Иными словами, задача RCPSP – это задача по определению дат раннего начала работ, удовлетворяющих следующим ограничениям:
1) условиям предшествования;
2) ограничения на ресурсы.
Кроме того, нередко встречаются задачи с ограничением на максимальное время продолжительности работ, т.е. дата финиша является навязанной.
Ограничения на ресурсы определяют подмножества работ, которые могут выполняться одновременно.
В рамках RCPSP существует 3 типа задач с ограничениями:
1) ограничен только 1 возобновляемый ресурс;
2) ограничено m возобновляемых ресурсов, при этом каждая работа может выполняться с использованием только 1 вида ресурсов;
3) ограничено m возобновляемых ресурсов, при этом каждая работа может выполняться с использованием k ресурсов.
Для решения проблем типа RCPSP используется 3 группы точных методов:
1) линейное программирование с использованием симплекс-метода для нахождения оптимального решения;
2) целочисленное линейное программирование с использованием метода границ и ветвей для нахождения оптимального решения;
3) «разумный» перебор возможных вариантов (решение нелинейной оптимизационной задачи).
При этом главным недостатком всех трех методов является то, что они эффективно работают только для небольших и относительно простых проектов, тогда как для сложных проектов время поиска решения выходит за рамки разумного.
Симплекс-метод
подразумевает последовательный перебор всех вершин области допустимых значений с целью нахождения той вершины, где функция принимает экстремальное значение. На первом этапе находится какое-нибудь решение, которое улучшается на каждом последующем шаге. Такое решение называется базисным.
|
|
|
Алгоритм:
1. Записать исходную задачу в форме основной задачи линейного программирования
2. В составленной симплекс-таблице необходимо просмотреть столбец со свободными членами. Если в нем имеются отрицательные элементы, то необходимо осуществить переход к 3 шагу, если же нет, то к 6.
3. необходимо определиться, какую переменную исключить из базиса, а какую включить, для того, что бы произвести перерасчет симплекс-таблицы. Производим итерации с отрицательными элементами в столбце со свободными членами.
4. пересчитываем всю симплекс-таблицу по специальным формулам
5. Если после перерасчета в столбце свободных членов остались отрицательные элементы, то переходим ко 2 шагу, если таких нет, то к 6.
6. если Вы дошли до 6 шага, значит нашли решение, которое допустимо. Однако, это не значит, что оно оптимально. Оптимальным оно будет только в том случае, если положительны все элементы в F-строке. Если же это не так, то необходимо улучшить решение, для чего находим для следующего перерасчета ведущие строку и столбец по следующему алгоритму.
7. Если невозможно найти ведущую строку, так как нет положительных элементов в ведущем столбце, то функция в области допустимых решений задачи не ограничена сверху и Fmax->∞. Если в строке F и в столбце свободных членов все элементы положительные, то найдено оптимальное решение.
ЦЛП
Целевая функция – минимизация даты
завершения последней работы
Ограничения:
o Отношения предшествования
o Ограничения на ресурсы
m,1|cpm|Cmax
cpm (фиксированная продолжительность работ) включает в себя ограничения (отношения предшествования и ограничения на ресурсы)
Пример:
Пусть А = множество работ, а M =  при условии, что i<j.
при условии, что i<j.
|
|
|
 | |||
| |||
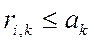
 - старт работы
- старт работы
 - финиш работы
- финиш работы
 - длительность работы
- длительность работы
 - ресурсы, необходимые для работы i(k)
- ресурсы, необходимые для работы i(k)
k – номер ресурса K=1,…,K
 - ограничение k ресурса (сколько всего)
- ограничение k ресурса (сколько всего)
Целевая функция  , где
, где 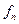 - это функция последней работы
- это функция последней работы
 (начало проекта)
(начало проекта)
Ограничения:
(1) в каждый момент времени необходимо знать по скольким работам нужно суммировать ресурсы.
(2)  должно действовать неравенство:
должно действовать неравенство: 
Так как мы не можем использовать эти формулировки для решения задач компьютерными программами, необходимо рассмотреть:
Формулировки задачи:

Целевая функция fn – дата финиша работы – ее минимум.

3. где LTF – поздний финиш с конфликтами, а ETF ранний финиш без конфликтов в расписании (считаем по CPM). И  .
.
q – время, которое отвечает за сдвиг работы вправо и влево. (так как t мы уже использовали, ввели q)
|
|
|


