 |
Билет № 14 Модель DCPM и задача DTCTP ( решение методом динамического программирования)
|
|
|
|
Дискретный случай DTCTP
· Работы имеют конечное число режимов выполнения (modes).
· Задачи DTCTP могут быть сформулированы как задачи целочисленного линейного программирования (ЦЛП), которые могут быть решены методом ветвей и границ.
· Точное решение проблемы занимает время, сравнимое с полным перебором всех возможных вариантов.
· Для нахождения приемлемых решений следует применять эвристические методы, например, модель DCPM.
Decision CPM
Это метод критического пути, при котором используется мультиработа или работа-решение.
Существует 2 варианта, первый, когда из кружочка выходит две работы и мы выполняем И ту И другую
И второй вариант, когда мы должны выбрать только одну работу ИЛИ ту ИЛИ другую
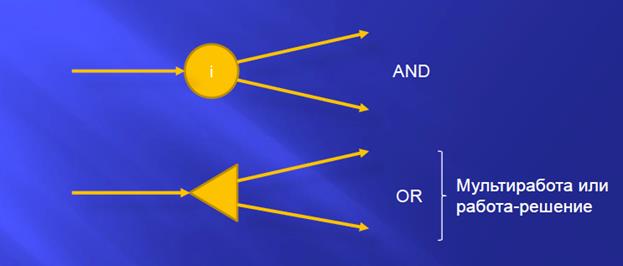
Модель разработана Crowston (MIT), Thompson (1967-1970).
Постановка задачи для DCPM
ü 𝑚𝑖𝑘 - режимы выполнения работы i, j=1,…,𝑘𝑖
ü Целевая функция – полные затраты проекта со штрафами/премиями
ü В ограничениях:
· Альтернатива: для любой i верно: сумма 𝑚𝑖𝑘𝑘=1
· Импликация: 𝑚𝑖𝑘≤𝑚𝑗𝑙
· Эквивалентность: 𝑚𝑖𝑘=𝑚𝑗𝑙
· Предшествование _𝑖→𝑗:
· 𝑠𝑖+𝑑𝑖≤𝑠𝑗, если i – обычная работа
· −𝑀∙1−𝑚𝑖𝑘+𝑠𝑖𝑘+𝑑𝑖𝑘≤𝑠𝑗, если i-мультиработа
Сначала необходимо найти критический путь.
Динамическое программирование для поиска критического пути
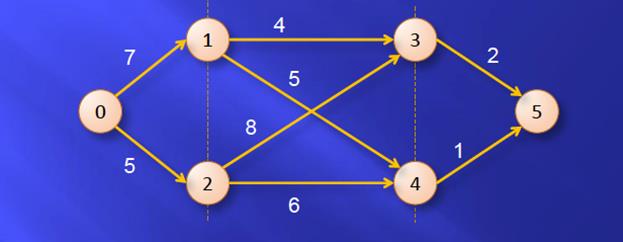
Ищем самый длинный путь, который ведет к 5 вершине, это будет критический путь.
В данном случае это путь 0-2-3-5.
В процессе подсчетов берем макс. длину путей из двух возможных. Делаем слева направо.
Fi(k) – слой(вершина)
F(0)=0
|
|
|
-F(v)- max p:p=v{f(p)+dpv}
Решение методом динамического программирования (Hindelang, Muth)
𝑌𝑖 - стоимость на i-м этапе (обратная прогонка) Начинаем с последней работы, так как есть мультиработы
𝑌𝑛= - 𝐶штраф/премия∙(𝛿𝑛 (навязанный финиш) −𝑠𝑛)
𝑌𝑖= сумма (𝐶𝑘+𝑌𝑘)∙𝑚𝑖𝑘 + сумма(C𝑗+𝑌𝑗) каждое предыдущее от большего номера к меньшему
A(i)– альтернативы мультиработы i
S(i)– прямые последователи работы I
𝐶𝑗 -оптимальные затраты работы j
ЦФ:𝑌1→ min в итоге дойдем до 1ого события и получим всю стоимость пути
Когда мы идем в обратную сторону на мультиработах выбираем минимум.
Алгоритм
ü AND (обычная работа)
o 𝐾𝐼(𝑡)= сумма (𝐾𝑋(𝑡+𝑡𝐼))+𝐶(𝐼) затраты
o 𝐿𝐼(𝑡)=max𝑋𝜖𝑆(𝐼){𝐿𝑋(𝑡+𝑡𝐼)} продолжительность
ü OR (мультиработа)
o 𝐾𝐼(𝑡)=min𝑋∈𝐴(𝐼){𝐶𝑋+𝐾𝑋(𝑡+𝑡𝐼)}
o 𝐿𝐼(𝑡)=𝑡𝐼+𝐿(𝑡+𝑡𝐼)
ü K– затраты, L-продолжительность
Стандартная задача k,l, когда нам заданы штрафы за просрочку.
Недостатки
Было доказано, что этот метод не приводит к оптимальному решению.
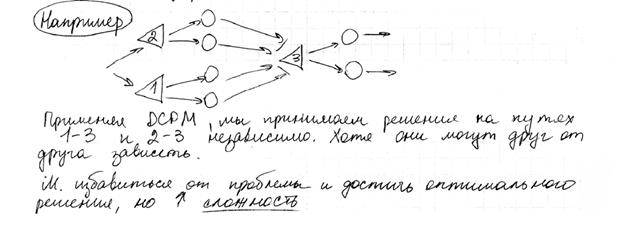
Расширенные задачи DTCTP
DTCTP-tsc (time-switch constraints)
Календари 8 часов/сутки; 24; без выходных
ü Yang & Chen (2000), Vanhoucke
DTCTP-wc (work continuity constraints)
Ограничение трудовых ресурсов на продолжительность работ
ü El-Rayes, Moselhi (1998)
Задача максимизации NPV
ü Herroelen, Demeulemeester, Van Dommelen (1997)
ü Затраты насчитываются на конец
Это же метод критической цепи= все работы выполняются как можно позже (часть работ должна выполняться позже- количество звеньев в критической цепи увеличится).
Билет № 15. Средства MS Project и Primavera для решения задачи RCPSP и TCTP.
RCPSP (Resource-Constrained Project Scheduling Problem) – занимается расчетом расписания проекта с ограничением на ресурсы.
|
|
|
RCPSP решает две задачи:
3. Когда продолжительность работ не зависит от количества ресурсов
4. Когда продолжительность работы зависит от количества ресурсов
TCTP
Ключевая проблема – нахождение компромисса между продолжительностью и стоимостью проекта.
Задачи для решения
4. Нахождение такого расписания проекта с заданной продолжительностью (навязанный финиш), которое позволит минимизировать стоимость его исполнения.
5. Нахождение такого расписания проекта с заданным бюджетным ограничением, которое позволит минимизировать продолжительность его выполнения.
Методы решения CPM-COST, Метод Гояла, ЗЛП
Project
|
|
|


