 |
Билет №9. Одновременная оптимизация проекта про времени и стоимости. Постановка задачи линейного программирования.
|
|
|
|
Значительный интерес представляет оптимизация сетевых графиков по времени и стоимости, в процессе которой решается вопрос, как уложиться в заданные ограничения по времени с минимальными дополнительными затратами. Оптимизация по времени и стоимости осуществляется с помощью PERT-COST.
Например, известно, что если сокращается продолжительность строительства, то при одновременном снижении накладных расходов прямые расходы возрастают. Функциональная зависимость между продолжительностью работ и их стоимостью пока точно не определена. Поэтому рассмотрим зависимость «время-стоимость» (с учетом прямых затрат), которая может быть определена условно.
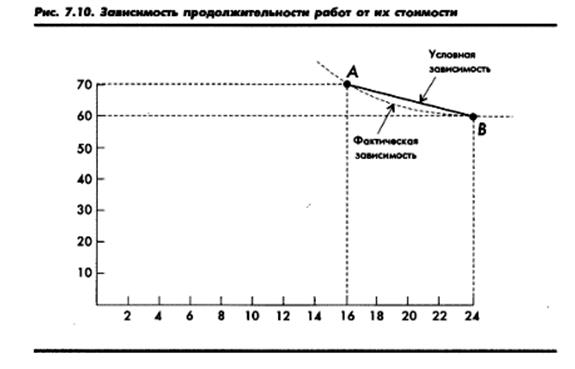
Как видно из рисунка, точка А соответствует наикратчайшему сроку выполнения данного проекта, то есть сроку, при котором все работы проводятся в предельно сжатые сроки.
Точка В соответствует нормальной продолжительности работ.
Затраты в точке А, так же как срок, считаются предельными: их дальнейшее увеличение лишь в очень незначительной степени повлияет на сокращение сроков. Затраты в точке В являются нормальными.
Прямая линия, соединяющая точки Аи В, точнее степень наклона этой прямой, и является характеристикой изменения величины прямых затрат при изменении продолжительности работ на единицу времени. Величина наклона для каждой единицы времени является величиной постоянной, так как мы приняли линейную зависимость между продолжительностью и стоимостью работ.
Величина наклона прямой определяется дробью, в числителе которой- разность между затратами в предельном и нормальном режимах, а в знаменателе- разность между продолжительностью работы в нормальном и предельном режимах. Для прямой, изображенной на рис. Эта величина составит:
|
|
|
(70-60): (24-16)= 1, 25 (тыс. Руб./день)
Также формулу можно записать так:
𝑔𝑟𝑎𝑑𝑖=𝑐𝑖−𝑐𝑖𝑑𝑖−𝑑𝑖>0
Для проведения оптимизации необходимо по каждой работе определить предельные и нормальные сроки выполнения, а также предельные и нормальные величины затрат. После этого методом последовательного приближения достичь заданного предельного срока за счет сокращения продолжительности критических работ, имеющих наименьшую величину удорожания.
Задачи для решения
1. Нахождение такого расписания проекта с заданной продолжительностью (навязанный финиш), которое позволит минимизировать стоимость его исполнения.
2. Нахождение такого расписания проекта с заданным бюджетным ограничением, которое позволит минимизировать продолжительность его выполнения.
Другие варианты решения
Эвристический метод CPM-COST
· Основная идея: Применение дополнительных средств и ресурсов может сократить продолжительность критического пути
· Основная цель: Ускорить время реализации проекта при минимальных затратах.
Алгоритм
· Расчет модели и определение критического пути
· Расчет градиента издержек для каждой работы критического пути
· Исключение из полученного списка тех работ, у которых отсутствует градиент издержек
· Начало процесса сокращения длительности работ с критической работы, которая имеет наименьший градиент издержек
· Отслеживать возможное появление нового критического пути
· Если в сети имеются два и более критических пути, то следует сокращать длительности на одну и ту же величину на всех параллельных критических путях.
Усовершенствованный метод (Goyal, 1996)
- Определение всех полных путей, которые нужно сократить (длина которых более требуемой продолжительности проекта)
- Расчет градиента для всех работ (которые входят хотя бы в один путь, найденный выше)
- Принятие решения о сокращении той работы, у которой наименьшее соотношение градиента и количества путей выбранных для сокращения, в которой присутствует эта работа
- Увеличение продолжительности тех работ, более раннее сокращение которых привело к чрезмерному сокращению выбранных путей
- Повторять с шага 3 до тех пор, пока не сократятся все выбранные пути. Отношение градиента к количеству путей из шага 3 необходимо пересчитывать, когда сокращается общее количество путей к сокращению в результате работы алгоритма.
|
|
|
Задача линейного программирования №1
𝐶 (𝑑1, …, 𝑑𝑛, 𝑠𝑛) = сумма (𝑏𝑖−𝑎𝑖∙𝑑𝑖) +𝑐0∙𝑠𝑛→min
- 𝑠𝑖+𝑑𝑖≤𝑠𝑗 если работа i предшествует работе j
- 𝑠1=0 ограничение на начало проекта
- 𝑠𝑖≥0 для каждой работы i
- 𝑑𝑖≤𝑑𝑖≤𝑑𝑖 для каждой работы i
- 𝑠𝑛≤𝛿𝑛 – дата навязанного финиша
|
|
|


