 |
Определители 2-го и3-го порядка и методы вычисления. Пример?.
|
|
|
|
Ответы по линейной алгебре.
Определение матрицы. Классификация матрицы: квадратная, диагональная, единичная, симметричная, ступенчатая, транспонированная?
Ø 1. Матрицей называется прямоугольная таблица размера nxm, состоящая из n строк и m столбцов, заполненная числами.
1)
 |
Квадратной матрицей называется матрица, у которой количество строк равно количеству столбцов (размера nxn), число n называется порядком матрицы. Пример,
2)
 |
Диагональной матрицей называется квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны 0. Пример,
3)
 |
Единичной матрицей называется диагональная матрица, диагональные элементы которой равны 1. Обозначают как Е. Пример,
4) Матрицу называют симметричной, если ее элементы симметричны относительно диагоналей матрицы. Симметричная матрица всегда квадратная и совпадает с ее транспонированной матрицей:
А = Ат.
5) Ступенчатой матрицей называется матрица, удовлетворяющая следующим условиям:
- если матрица содержит нулевую строку, то все строки, расположенные под нею, так же нулевые;
 |
- если первый ненулевой элемент некоторой строки расположен в столбце с номером i, и следующая строка не нулевая, то первый ненулевой элемент следующей строки должен находиться в столбце с номером больше, чем i. Пример,
 |
6) Транспонированная матрица – матрица АT, полученная из исходной матрицы А oзаменой строк на столбцы. Например,
Матрица и основные действия над ними. Пример умножения двух матриц?
Ответ:
1) Сложение.
Операция сложения матриц вводится только для матриц одинаковых размеров.
Суммой двух матриц Аmxn = (aij) и Вmxn= (bij) называется матрица Cmxn= (cij), такая, что cij = aij + bij (I = 1, m, j = 1, n).
|
|
|
Пример 1.2.
 |
Аналогично определяется разность матриц.
Умножение на число.
Произведением матрицы Аmxn = (aij)на число к называется матрица Вmxn = (bij), такая, что bij = k•aij (i=1, m, j=1, n).
 |
Пример 1.3.
Матрица –А = (-1).
Разность матрице А-В можно определить так: А-В = А +(-В). Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:
1. А+В=В+А
2. А+(В+С)=(А+В)+С
3. А+О=А
4. А-А=О
5. 1•А=А
6. α•(A+B)=αA+αB
7. (α+β)•A=αA+β
8. α(βA)=(αβ)•A,
где А, В, С – матрицы, α и β – числа.
Элементарные преобразования над матрицей. Эквивалентные матрицы. Приведение матрицы к ступенчатому виду?
Ответ:
Элементарными преобразованиями матриц являются:
- перестановка местами двух параллельных рядов матрицы;
- умножение всех элементов ряда матриц на число, отличное от нуля;
- прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
✔Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается А~В.
При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например,
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 0
4.Невырожденные матрицы. Определение и алгоритм нахождения обратной матрицы?
Ответ:
✔Квадратная матрица А называется невырожденной, если определитель 🔺= det не равен нулю: 🔺= det A ≠0. В противном случае (🔺=0) матрица А называется вырожденной.
✔Матрицей, союзной к матрице А, называется матрица
А11А21... Аn1
А12А22... Аn2
А*= А13 А23... Аn3
А1n А24... Аn4
где Аij = алгеброическое дополнение элемента аij данной матрицы А (оно определяется так же, как и алгебраическое дополнение элемента определителя).
|
|
|
✔Матрица А-1 называется обратной матрице А, если выполняется условие:
А . А-1= А-1. А = Е.
Где Е – единичная матрица того же порядка, что и матрица А. Матрица А-1 имеет те же размеры, что и матрица А.
Определители 2-го и3-го порядка и методы вычисления. Пример?.
Квадратной матрице А порядка n можно сопоставить число det А (или | A |, или  ), называемое ее определителем, следующим образом:
), называемое ее определителем, следующим образом:

Определитель матрицы A также называют ее детерминантом. Правило вычисления детерминанта для матрицы порядка N является довольно сложным для восприятия и применения. Однако известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителя по элементам некоторого ряда (свойство 7). При этом заметим, что определители невысоких порядков (1, 2, 3) желательно уметь вычислять согласно определению.
Вычисление определителей второго порядка.
Определитель второго порядка (матрицы размера 2 на 2) вычисляется по правилу:

Запомнить просто: произведение элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной.
Пример:
 .
.
Вычисление определителей третьего порядка.
Определитель третьего порядка вычисляется по правилу:

Запомнить порядок сомножителей, конечно же, очень трудно, если не знать визуального представления этого правила, которое называется правило треугольников:

Здесь схематично показано, какие сомножители соседствуют в слагаемых.
Пример:
Вычислить определитель:

Решение:
Воспользуемся правилом треугольников.
Объясним картинку подробно, т.е. распишем каждое слагаемое отдельно:













Итого: 
Ответ: 108
6. Определители 2-го и 3-го порядка и их основные свойства?
6) Сформулируем основные свойства определителей, присущих определителям всех порядков. Некоторые из этих свойств поясним на опредлителях 3-го порядка.
Свойство 1 («Равноправность строк и столбцов»):
Определитель не изменится, есл его строки заменить столбцами, и наоборот. Иным словами,
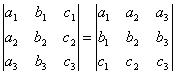
СВОЙСТВО 2. При перестановке двух параллельных рядов определитель меняет знак.
|
|
|
СВОЙСТВО 3. Определитель, имеющий два одинаковых ряда, равен нулю.
СВОЙСТВО 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.
▲ Действительно,

Свойство 5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
Например,

Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одною ряда прибавить соответствующие элементы параллельного ряда, умноженные па любое число.
Пример 4.3. Доказать, что

Решение: Действительно, используя свойства 5, 4 и 3 подучим

Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения.
|
|
|


