Общий вид систем линейных однородных алгебраических уравнений; понятие решения системы условия и совместности и методы решения?

Ответ напрашивается сам собой. Система линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю. Например:
Однородная система в с е г д а с о в м е с т н а, поскольку любая однородная линейная система имеет по крайней мере одно решение:

x₁=0, x₂=0,..., x_n=0.

Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называется нетривиально совместной.

Доказано, что при m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю.

ПРИМЕР 1. Нетривиальная совместность однородной системы линейных уравнений с квадратной матрицей.

Применив к матрице системы алгоритм гауссова исключения, приведем матрицу системы к ступенчатому виду

Число r ненулевых строк в ступенчатой форме матрицы называется рангом матрицы, обозначаем
r=rg(A) или r=Rg(A).

Справедливо следующее утверждение.

Для того, чтобы однородная система была нетривиально совместна, необходимо и достаточно, чтобы ранг r матрицы системы был меньше числа неизвестных n.

ПРИМЕР 2. Нетривиальная совместность однородной системы трех линейных уравнений с четырьмя неизвестными.

Если однородная система нетривиально совместна, то она имеет бесконечное множество решений, причем линейная комбинация любых решений системы тоже является ее решением.
Доказано, что среди бесконечного множества решений однородной системы можно выделить ровно n-r линейно независимых решений.
Совокупность n-r линейно независимых решений однородной системы называется фундаментальной системой решений. Любое решение системы линейно выражается через фундаментальную систему. Таким образом, если ранг r матрицы A однородной линейной системы Ax=0 меньше числа неизвестных n и векторы
e₁, e₂,..., e_n-r образуют ее фундаментальную систему решений (Ae_i=0, i=1,2,..., n-r), то любое решение x системы Ax=0 можно записать в виде

x=c₁e₁+ c₂e₂+... + c_n-re_n-r,

где c₁, c₂,..., c_n-r — произвольные постоянные. Записанное выражение называется общим решением однородной системы.

Исследовать однородную систему — значит установить, является ли она нетривиально совместной, и если является, то найти фундаментальную систему решений и записать выражение для общего решения системы.

Исследуем однородную систему методом Гаусса.

Пусть

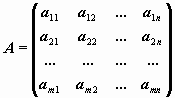
матрица исследуемой однородной системы, ранг которой r< n.

Такая матрица приводится Гауссовым исключением к ступенчатому виду

.

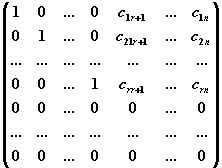Соответствующая эквивалентная система имеет вид

Отсюда легко получить выражения для переменных x₁, x₂,..., x_r через x_r+1, x_r+2,..., x_n. Переменные
x₁, x₂,..., x_r называют базисными переменными, а переменные x_r+1, x_r+2,..., x_n — свободными переменными.

Перенеся свободные переменные в правую часть, получим формулы

которые определяют общее решение системы.

Положим последовательно значения свободных переменных равными

и вычислим соответствующие значения базисных переменных. Полученные n-r решений линейно независимы и, следовательно, образуют фундаментальную систему решений исследуемой однородной системы:

9. Система двух линейных однородных уравнений от трех неизвестных: определение и решение методом Крамера?

 

Пусть нам требуется решить систему линейных алгебраических уравнений

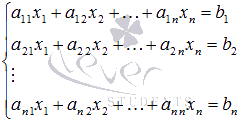
в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть, .

Пусть 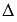- определитель основной матрицы системы, а - определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов:

При таких обозначениях неизвестные переменные вычисляются по формулам метода Крамера как . Так находится решение системы линейных алгебраических уравнений методом Крамера.

Пример.

Решите систему линейных уравнений методом Крамера .

Решение.

Основная матрица системы имеет вид 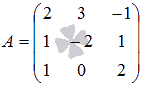. Вычислим ее определитель (при необходимости смотрите статью определитель матрицы: определение, методы вычисления, примеры, решения):

Так как определитель основной матрицы системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера.

Составим и вычислим необходимые определители 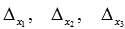(определитель получаем, заменив в матрице А первый столбец на столбец свободных членов , определитель - заменив второй столбец на столбец свободных членов, - заменив третий столбец матрицы А на столбец свободных членов):

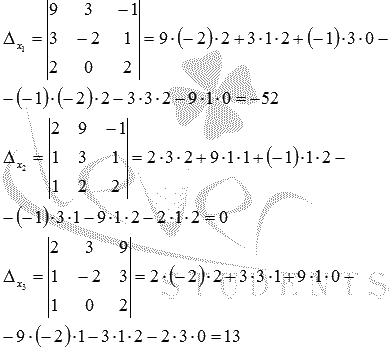
Находим неизвестные переменные по формулам :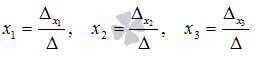

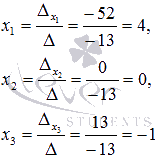
Ответ:

x₁ = 4, x₂ = 0, x₃ = -1.

Основным недостатком метода Крамера (если это можно назвать недостатком) является трудоемкость вычисления определителей, когда число уравнений системы больше трех.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: