 |
Рекомендации по организации самостоятельной работы студентов
|
|
|
|
При изучении данного курса можно пользоваться любым учебным пособием по алгебре для студентов математических факультетов университетов и педагогических вузов. В списке литературы указаны некоторые из них, наиболее соответствующие содержанию курса и уровню математической подготовки аудитории.
Учебник Л.Я. Куликова [3] полностью соответствует программе, но написан довольно сложным языком. Учебное пособие Д.К. Фаддеева [4] написано менее формально. Одним из его достоинств является удобный для первого знакомства порядок следования разделов, при котором происходит плавный переход от рассмотрения конкретных объектов к более абстрактным понятиям. Не потерял своей актуальности и классический учебник А.Г. Куроша [14]. Более современное изложение алгебры, содержащее материал, выходящий за рамки данного курса, можно найти у А.И. Кострикина [2]. При изучении теории делимости и сравнений целых чисел рекомендуем использовать лаконичный классический учебник И.М. Виноградова [1].
Для первоначального знакомства мы рекомендуем также использовать серию пособий [9]–[12], где наряду с более тщательным отбором материала стиль его изложения менее формальный. Он сопровождается большим количеством пояснений, отступлений, иллюстрирующих примеров.
Перечислим по разделам привязку материала к учебникам.
1. Элементы теории множеств, математической логики, числовых систем – [3], [9].
2. Основные алгебраические структуры – [3], [9], [10].
3. Системы линейных уравнений. Арифметическое n -мерное векторное пространство – [3], [9].
4. Матрицы и определители – [3], [9].
5. Векторные пространства – [3], [10].
6. Евклидовы пространства – [3], [10].
7. Линейные отображения и линейные операторы – [3], [10].
|
|
|
8. Теория делимости целых чисел – [1], [12].
9. Теория сравнений – [1], [12].
10. Комплексные числа – [3], [4], [14].
11. Многочлены от одной переменной – [3], [11].
12. Многочлены от нескольких переменных – [3], [11], [14].
13. Многочлены над числовыми полями – [3], [11], [14].
14. Расширения полей – [3], [11].
15. Элементы теории групп – [3], [10].
16. Кольца и поля – [3], [14], [12].
17. Элементы теории делимости в целостных кольцах – [3], [12].
18. Поле частных целостного кольца – [3], [12].
Для создания целостного представления обо всём курсе в Приложении содержится план-конспект курса, в котором, наряду с подробным изложением содержания курса (а там приведены формулировки всех утверждений, которые мы намерены доказать), сделаны указания по поводу их доказательства, указаны подробные планы и идеи проведения доказательства.
Рекомендуемая литература
Основная литература
1. Виноградов И.М. Основы теории чисел. М.: Наука, 1974.
2. Кострикин А.И. Введение в алгебру. М.: Наука, 1977.
3. Куликов Л.Я. Алгебра и теория чисел. М.: Высшая школа, 1979.
4. Фаддеев Д.К. Лекции по алгебре. М.: Наука, 1984.
5. Куликов Л.Я., Москаленко А.И., Фомин А.А. Сборник задач по алгебре и теории чисел. М.: Просвещение, 1993.
6. Проскуряков И.В. Сборник задач по линейной алгебре. М.: Наука, 1984.
7. Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. М.: Наука, 1977.
8. Моисеев С.А., Суворов Н.М. Задачник-практикум по алгебре и теории чисел. Рязань: Изд-во РГУ, 2006.
Дополнительная литература
9. Варпаховский Ф.Л., Солодовников А.С. Алгебра. Элементы теории множеств. Линейные уравнения и неравенства. Матрицы и определители. М.: Просвещение, 1974.
10. Варпаховский Ф.Л., Солодовников А.С., Стеллецкий И.В. Алгебра. Группы, кольца, поля. Векторные и евклидовы пространства. Линейные отображения. М.: Просвещение, 1978.
11. Винберг Э.Б. Алгебра многочленов. М.: Просвещение, 1980.
12. Казачек Н.А., Перлатов Г.Н., Виленкин Н.Я., Бородин А.И. Алгебра и теория чисел. М.: Просвещение, 1984.
|
|
|
13. Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия. М.: Наука, 1986.
14. Курош А.Г. Лекции по общей алгебре. М.: Наука, 1973.
15. Мальцев А.И. Основы линейной алгебры. М.: Наука, 1970.
16. Постников М.М. Теория Галуа. М.: Физматгиз, 1963.
17. Окунев Л.Я. Сборник задач по высшей алгебре. М.: Просвещение, 1964.
17. Сборник задач по алгебре: Учебное пособие /Под ред. А.И.Кострикина. М.: Факториал, 1995.
Приложение 1.
План-конспект курсов алгебры и теории чисел и избранных вопросов алгебры
ГЛАВА 1. Элементы теории множеств, математической логики, числовых систем
Множества, элементы, подмножества
Множества и элементы. a Î A. Конечные и бесконечные множества. Способы задания множества. { a 1, a 2,..., an }, { x êj(x)}. N, Z, Q, R, C, R +, R *.
Равенство и неравенство множеств. Подмножества. A Ì B. Пустое и универсальное множества. Æ, U.
Теорема. Свойства включения.
1°. A Ì A.
2°. A Ì B Ù B Ì C Þ A Ì C.
3°.ÆÌ A, A ÌU.
4°. A Ì B Ù B Ì A Û A = B. 
5°. Пустое множество единственное.
Операции над множествами
Пересечение, объединение, разность симметрическая разность двух множеств. Дополнение множества. Ç, È, \, ¯. Диаграммы Эйлера-Венна.
Теорема. Свойства операций.
1°. A Ç A = A;
2°. A Ç B = B Ç A;
1¢. A È A = A;
2¢. A È B = B È A;
3°. (A Ç B)Ç C = A Ç(B Ç C);
4°. A Ç(B È C) = (A Ç B)È(A Ç C);
5°. A \(B Ç C) = (A \ B)È(A \ C);
6°.  ;
;
7°. A Ç(A È B) = A;
8°. A Ç 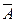 = Æ;
= Æ;
9°. A ÇÆ = Æ, A ÇU = A;
3¢. (A È B)È C = A È(B È C);
4¢. A È(B Ç C) = (A È B)Ç(A È C);
5¢. A \(B È C) = (A \ B)Ç(A \ C);
6¢.  ;
;
7¢. A È(A Ç B) = A;
8¢. A È 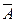 = U;
= U;
9¢. A ÈU = U, A ÈÆ = A;
10°.  = A;
= A;
11°. A Ì B Û A Ç B = A Û A È B = B;
|
|
|


