Формула для обратной матрицы. Теорема Крамера

 

Теорема 1. Формула для вычисления обратной матрицы.

Если квадратная матрица А невырожденная, то

А ^–1 = .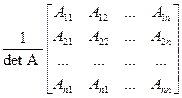

 

Теорема 2. Теорема Крамера.

Если в системе n линейных уравнений с n неизвестными матрица коэффициентов невырожденная, то система имеет единственное решение, которое задаётся формулами x_k = 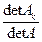, где матрица A_k получается из матрицы A заменой k -го столбца столбцом свободных членов.

 

Определитель произведения матриц

 

Теорема.

Если A и B – квадратные матрицы одного формата, то det(AB) = det A ×det B.

 

Лемма. Если E _j – матрица элементарного преобразования j, то det(E _j B) = det E _j×det B.

 

Теорема о ранге матрицы

 

Обобщение понятия минора. M .

 

Теорема. Ранг матрицы равен наибольшему из порядков её ненулевых миноров.

 

План доказательства

1. Если – базис системы вектор-строк, то существуют столбцы с номерам p ₁, p ₂,..., p_r такие, что M ¹ 0.

2. M = 0 для любого k ´ k - минора, если k > r.

 

ГЛАВА 5. Векторные пространства

 

Определение, примеры, простейшие свойства векторных пространств

 

Определение векторного пространства.

Важнейшие примеры.

1. R ^{2, 3}. 2. Pⁿ. 3. 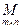. 4. F _R. 5. R [ x ]. 6. R _n [ x ]. 7. Поле над любым своим подполем. 8. 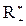над R.

 

Теорема. Простейшие свойства векторных пространств.

Совпадает с теоремой 3.2.2.

 

Линейная зависимость и линейная независимость систем векторов. Базис и ранг системы векторов

 

Содержание этого параграфа полностью повторяет содержание параграфов 3.3. и 3.4.

 

Конечномерные векторные пространства. Изоморфизм векторных пространств. Координаты вектора в некотором базисе

 

Примеры конечномерных и бесконечномерных векторных пространств. Размерности этих конечномерных векторных пространств.

 

Теорема 1. Любая ненулевая система векторов конечномерного векторного пространства обладает базисом. Количество векторов этого базиса не превосходит размерности пространства.

 

Координаты вектора в базисе Е. Столбец координат [ a ] _E. Равенство a = E ×[ a ] _E.

 

Теорема 2. Свойства координат.

1°. [ a + b ] = [ a ]+[ b ].

2°. [a a ] = a[ a ].

 

Изоморфизм векторных пространств. Отношение изоморфизма.

 

Пример.

Если V – n -мерное векторное пространство над полем P и E – базис V, то отображение j: a [ a ] _E является изоморфизмом V на Pⁿ.

 

Теорема 3. Свойства изоморфизма векторных пространств.

Содержание этой теоремы и его доказательство полностью повторяет содержание теоремы 2.3.3.

 

Теорема 4. Свойства векторов и их систем, сохраняемые при изоморфизмах.

1°. При изоморфизме нуль-вектор переходит в нуль-вектор.

2°. При изоморфизме противоположный вектор переходит в противоположный вектор.

3°. Изоморфизм сохраняет линейную комбинацию.

4°. Изоморфизм сохраняет линейную зависимость.

5°. Изоморфизм сохраняет линейную независимость.

6°. Изоморфизм сохраняет базисы.

 

Теорема 5. Критерий изоморфизма конечномерных векторных пространств.

Два конечномерных векторных пространства над одним и тем же полем изоморфны тогда и только тогда, когда равны их размерности.

 

Связь между различными базисами конечномерных векторных пространств. Координаты вектора в разных базисах

 

Матрица перехода от одного базиса к другому М = М_Е (Е ¢): Е ¢ = Е × М.

 

Теорема 1. Критерий матрицы перехода.

n ´ n -матрица А служит матрицей перехода от одного базиса n -мерного пространства к другому тогда и только тогда, когда А невырожденная матрица.

 

Координаты вектора в разных базисах.

 

Теорема 2. Связь между координатами вектора в разных базисах.

[ a ] _{Е ¢} = М_Е ^–1(Е ¢)×[ a ] _E.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: