ГЛАВА 8. Теория делимости целых чисел

 

§ 1. Отношение делимости. Деление с остатком

 

Определение делимости целых чисел. a b, b | a.

 

Теорема 1. Свойства делимости.

 

Для любых целых чисел имеют место следующие соотношения

1°. a a.

2°. a 1.

3°. a b Þ ± a ± b.

4°. 0 a;

5°. a b Ù b c Þ a c.

6°. a b Ù b c Þ ua+vb c.

7°. a ¹ 0Ù a b Þ ³ .

8° a ¹ 0Ù b ¹ 0Ù a b Ù b a Þ a = ± b.

 

Определение деления с остатком.

 

Теорема 2. О делении с остатком.

 

Любое целое число a можно разделить с остатком на любое целое число b ¹ 0. Это деление осуществляется единственным образом.

 

Определение систематического представления натурального числа.

 

Теорема 3. Любое целое неотрицательное число a может быть представлено, причем единственным образом, в виде

a = a_ngⁿ + a_{n –1} g^{n –1}+... + a ₁ g + a ₀,

где g Î N, g ¹1, 0 £ a_k £ g –1 при всех 0 £ k £ n.

 

Запись:

 

Таблицы сложения и умножения в g -ичной системе счисления.

 

Перевод из одной системы счисления в другую: правила деления и умножения.

 

§ 2. НОД чисел. Алгоритм Евклида

 

ОД и НОД системы чисел.

 

Теорема 1. Единственность НОД.

 

Любые два НОД системы чисел совпадают, с точностью до знака, если они существуют.

 

(a ₁, a ₂,..., a_n).

 

Алгоритм Евклида: описание алгоритма, конечность алгоритма.

 

Теорема 2. Существование НОД двух чисел.

 

Для любых двух целых чисел, не равных нулю одновременно, их НОД существует. Он равен последнему, отличному от нуля, остатку алгоритма Евклида для этих двух чисел.

 

Следствие 1. Свойства НОД.

 

1°. С точностью до знака,(ac, bc) = (a, b) c.

2°. Если t – ОД(a, b), то, с точностью до знака, .

3°. Если d = (a, b), то 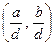= 1.

4°. Если d = (a, b), то существуют числа u, v такие, что ua + vb = d.

5°. Наибольший по модулю общий делитель чисел a и b является их НОД.

 

Теорема 3. Цепное правило.

 

НОД нескольких чисел a ₁, a ₂,..., a_n существует. Он вычисляется по правилу ((... ((a ₁, a ₂), a ₃),..., a_{n –1}), a_n).

 

Следствие 2. Свойства НОД 1°–5° двух чисел справедливы для любого конечного количества чисел.

 

§ 3. Взаимно простые числа

Теорема 1. Критерий взаимной простоты чисел.

 

Числа a и b взаимно простые тогда и только тогда, когда существуют целые числа u и v такие, что ua + vb = 1.

 

Теорема 2. Свойства взаимно простых чисел.

 

1°. (a, c) = (b, c) = 1 Þ (ab, c) = 1.

2°. ab c Ù(a, c) = 1 Þ b c.

3°. a b Ù a c Ù(b, c) = 1 Þ a bc.

Обобщение результатов теорем 1 и 2 на случай n чисел.

 

§ 4. НОК чисел

 

ОК и НОК системы чисел.

 

Теорема 1. Единственность НОК.

 

Любые два НОК системы чисел совпадают, с точностью до знака, если они существуют.

 

[ a ₁, a ₂,..., a_n ].

 

Теорема 2. Существование НОК двух чисел.

 

Для любых двух целых чисел a и b, не равных нулю одновременно, их НОК существует. Он равен .

 

Следствие 1. Свойства НОК двух чисел.

 

1°. С точностью до знака,[ ac, bc ] = [ a, b ] c.

2°. Если t – ОД(a, b), то, с точностью до знака, ;

3°. Наименьшее по модулю общее кратное чисел a и b является их НОК.

 

Теорема 3. Цепное правило.

 

НОК нескольких чисел a ₁, a ₂,..., a_n существует. Оно вычисляется по правилу [[... [[ a ₁, a ₂], a ₃],..., a_{n –1}], a_n ].

 

Следствие 2. Свойства НОК 1°–3° двух чисел справедливы для любого конечного количества чисел.

 

§ 5. Простые числа. Основная теорема арифметики

 

Простые и составные числа.

 

Теорема 1. Свойства простых чисел.

 

1°. p – простоеÙ p a Þ a = 1Ú a = p.

2°. Если p ₁, p ₂ – различные простые числа, то ни одно из них не делится на другое.

3°. p – простое Þ (" a)(a p Ú(a, p) = 1).

4°. a ₁ a ₂... a_n p Þ a ₁ p Ú a ₂ p Ú... Ú a_n p.

5°. (" a ¹1)($ p)(p – простоеÙ a p).

6°. Если a ¹ 1 и a не делится ни на одно простое число p £ , то a – простое число.

 

Теорема 2. Основная Теорема Арифметики.

 

Всякое натуральное число, отличное от единицы, либо является простым числом, либо представляется в виде произведения простых чисел, причем такое представление единственное, с точностью до порядка следования множителей.

 

Каноническое разложение (факторизация) натурального числа.

 

Следствие 1. Всякое натуральное составное число имеет единственное каноническое разложение.

 

Следствие 2. Если a имеет каноническое разложение a = , то b | a Û b = , где 0 £ b _i £ a _i для всех i = .

 

Следствие 3. Правила отыскания НОД и НОК.

Пусть a = , b = – почти канонические разложения чисел a и b, то есть для всех i = 0 £ a _i, 0 £ b _i причем одно из них ¹ 0. Тогда

1°. (a, b) = , где (" i = )(g_i = min{a _i, b _i }.

2°. [ a, b ] = , где (" i = )(d_i = max{a _i, b _i }.

 

Теорема 3. Множество простых чисел бесконечно.

 

Доказательство Евклида.

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: