Геометрическое изображение комплексных чисел

 

Действительная и мнимая части, модуль и аргумент комплексного числа. Связь между ними.

 

Тригонометрическая форма комплексного числа.

 

Теорема. Всякое комплексное число единственным образом представляется в тригонометрической форме.

 

Свойства модуля комплексного числа, связанные со сложением и вычитанием.

 

Тригонометрическая форма комплексного числа

Теорема 1. Если z ₁ = r ₁(cos j₁+ i sin j₁), z ₂ = r ₂(cos j₂+ i sin j₂), то

а) z ₁ z ₂ = r ₁ r ₂ (cos (j₁+j₂)+ i sin (j₁+j₂)); б) = (cos (j₁–j₂)+ i sin (j₁–j₂)).

 

Следствие.

 

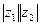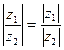= , ; arg (z ₁ z ₂) = arg z ₁+arg z ₂, arg = arg z ₁–arg z ₂.

 

Теорема 2. Формулы Муавра.

 

1°. Если z = r (cos j+ i sin j), n Î N, то zⁿ = rⁿ (cos n j+ i sin n j).

2°. Если z = r (cos j+ i sin j), n Î Z, то zⁿ = rⁿ (cos n j+ i sin n j).

 

Комплексно сопряжённые числа

 

Теорема. Свойства комплексно сопряжённых чисел.

 

1°. Re = Re z, Im = –Im z.

2°. , arg = –arg z.

3°. = z.

4°. z Î R Û = z.

5°. + z Î R, × z Î R.

6°. z ₁+ z ₂Î R Ù z ₁× z ₂Î R Þ z ₁,× z ₂Î R Ú z ₁ = .

7°. для любой арифметической операции *.

8°. Если комплексное число w получено из комплексных чисел z ₁, z ₂,..., z_n с помощью четырёх арифметических операций: w = f (z ₁, z ₂,..., z_n), то, заменив числа z ₁, z ₂,..., z_n на числа, комплексно сопряжённые им, и проделав те же операции, и в том же порядке, получим число, комплексно сопряжённое w: .

 

Корни из комплексных чисел

 

Теорема. Пусть z Î C, z ¹ 0, n Î N, n > 1. Тогда существует в точности n корней степени n из числа z. Если z = r (cos j+ i sin j) – тригонометрическая форма z, то все корни могут быть найдены по формуле

. (1)

 

Этапы доказательства:

1) очерчивание круга поиска; 2)числа вида (1) различны;

3) любой корень степени n из z совпадает с одним из чисел (1).

 

Корни из единицы. . Первообразные корни.

 

Теорема. Свойства корней из единицы.

 

1°. Произведение и частное корней степени n из единицы также являются корнями степени n из единицы.

2°. Если w – один из корней степени n из числа z, то множество всех корней степени n из числа z может быть получено умножением w на значения корней степени n из единицы: .

3°. Для любого n Î N существует первообразный корень степени n из единицы: e₁ = соs + i sin .

4°. Число eÎ является первообразным корнем из единицы тогда и только тогда, когда все числа e⁰ = 1, e¹, e²,..., e ^{n –1} различны.

5°. Сумма всех корней степени n из ненулевого числа равна нулю.

 

ГЛАВА 11. Кольцо многочленов от одной переменной

 

Определение многочлена

 

Многочлен как бесконечная последовательность элементов кольца А, в которой только конечное число элементов отлично от нуля. М_А. Операции сложения и умножения многочленов. Степень многочлена. deg f.

 

Теорема 1. Наследование свойств кольца.

 

1°. Сумма и произведение двух многочленов над кольцом также являются многочленами.

2°. Алгебра многочленов á М_А; +, ×ñ над кольцом также является кольцом.

3°. Если кольцо А коммутативно или ассоциативно, или кольцо с единицей, или целостное кольцо, то этим же свойством обладает кольцо á М_А; +, ×ñ.

 

Теорема 2. Свойства степени многочлена.

 

1°. deg(f ± g) £ max {deg f, deg g }.

2°. deg(f × g) £ deg f + deg g.

3°. Если кольцо А целостное, то deg(f × g) = deg f + deg g.

 

Многочлен x. Натуральные степени многочлена x. Стандартная форма многочлена: a_nxⁿ + a_{n –1} x ^{n –1}+... + a ₁ x + a ₀. Условие равенства двух многочленов, записанных в стандартной форме. А [ x ].

 

Многочленные функции

 

Многочленная функция : А ® А, соответствующая многочлену f.

Теорема. Свойства кольца многочленных функций.

 

1°. Множество всех многочленных функций является подкольцом в кольце всех функций F_A, отображающих А в А.

2°. Соответствие F: f является эпиморфизмом кольца многочленов А [ x ] на кольцо многочленных функций .

3°. Для конечного кольца А соответствие F изоморфизмом не является.

 

§ 3. Деление многочлена на двучлен х- -a. Схема Горнера

 

Теорема 1. Если f Î A [ x ], aÎ A, то многочлен f (x) можно, причём единственным образом, представить в виде

f = (х –a) g (x)+ r,

где g Î A [ x ], r Î A. При этом r = (a).

 

Схема Горнера.

 

Разложение многочлена по степеням двучлена х –a.

 

Теорема 2. Если f Î A [ x ], aÎ A, то многочлен f можно, причём единственным образом, разложить по степеням двучлена х –a.

 

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: