 |
Операции над линейными отображениями
|
|
|
|
Сумма и произведение (композиция) линейных отображений. Произведение линейного отображения на элемент поля.
Теорема 1. Свойства операций над линейными отображениями.
1°. Сумма и произведение линейных отображений, а также произведение линейного отображения на скаляр, являются линейными отображениями.
2°. Множество всех линейных отображений векторного пространства V 1 в векторное пространство V 2 является векторным пространством над тем же полем относительно операций сложения линейных отображений и умножения на скаляр.
3°. Множество всех линейных преобразований (линейных функционалов) векторного пространства в себя является кольцом относительно операций сложения и умножения.
Теорема 2. Связь линейных отображений и их матриц.
Если V 1, V 2 и V 3 – конечномерные векторные пространства над одним и тем же полем, E 1, E 2 и E 3 – их базисы, соответственно, то:
а) j: V 1 ® V 2 – изоморфизм Û M j(E 1, E 2) – невырожденная;
б) M lj(E 1, E 2) = l× M j(E 1, E 2);
в) M j+y(E 1, E 2) = M j(E 1, E 2)+ M y(E 1, E 2);
г) M j 
y(E 1, E 2) = M j(E 1, E 2)× M y(E 2, E 3).
Ранг, дефект, ядро и образ линейного отображения
Ядро и образ линейного отображения j. Ker j. Im j. Ранг и дефект линейного отображения. r (j). d (j).
Теорема 1. Ядро и образ линейного отображения j: V 1 ® V 2 являются подпространствами векторных пространств V 1 и V 2, соответственно.
Теорема 2. Ранг линейного отображения конечномерного векторного пространства равен рангу матрицы линейного отображения.
Теорема 3. Если j: V 1 ® V 2 – линейное отображение конечномерного векторного пространства, то сумма ранга и дефекта этого отображения равна размерности пространства V 1: dim V 1 = r (j)+ d (j).
Линейные операторы
|
|
|
Теорема 1. Всякий инъективный линейный оператор конечномерного векторного пространства сюръективен и наоборот.
Подобие матриц.
Теорема 2. Две квадратные матрицы подобны тогда и только тогда, когда они являются матрицами одного и того же линейного оператора, но в разных базисах.
Линейные алгебры
Определение линейной алгебры.
Важнейшие примеры.
1. 
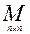. 2. End V. 3. R [ x ]. 4. F R.
Изоморфизм линейных алгебр. Стандартные свойства изоморфизма линейных алгебр (см. теоремы 5.3.3 и 5.3.4).
Теорема. Алгебра всех линейных операторов n -мерного векторного пространства над полем Р изоморфна алгебре n ´ n -матриц над этим же полем.
Собственные векторы и собственные значения линейного оператора
Инвариантные подпространства линейного оператора. Примеры. Собственные векторы и собственные значения линейного оператора. Геометрическая интерпретация.
Корневое (собственное) подпространство К (l).
Теорема 1. Свойства собственных векторов.
1°. К (l) является подпространством векторного пространства.
2°. Собственные векторы, принадлежащие различным собственным значениям, ЛНЗ.
3°. Для любого линейного оператора конечномерного векторного пространства сумма размерностей всех его корневых подпространств не превышает размерности всего пространства.
4°. Линейный оператор имеет диагональную матрицу в некотором базисе тогда и только тогда, когда этот базис состоит из собственных векторов линейного оператора.
Характеристический многочлен матрицы. Характеристический многочлен линейного оператора.
Теорема 2. Корректность определения характеристического многочлена линейного оператора.
1°. Подобные матрицы имеют одинаковые характеристические многочлены.
2°. Определения характеристического многочлена линейного оператора корректно.
Теорема 3. Правила отыскания собственных векторов и собственных значений линейного оператора.
|
|
|
1°. Множество собственных значений линейного оператора совпадает с множеством корней характеристического многочлена.
2°. Собственное подпространство К (l) совпадает с множеством решений однородной системы линейных уравнений (A –l E)× X = q.
|
|
|
